A Reconfigurable FPGA Architecture for DSP Transforms Subramanian

A Reconfigurable FPGA Architecture for DSP Transforms Subramanian Rama Vishnu Vijayaraghavan

OUTLINE n n n n Motivation Reconfigurable FPGA’s DSP Transforms, Breakdown & Applications Communication Graphs& Proposed Architecture Imaginary Radix Complex Multiplication Accomplished Work Conclusion

Motivation n Dedicated VLSI Architectures for Orthogonal Transforms – FFT, DCT, Convolution, Correlation Dedicated VLSI Architectures for Non. Orthogonal Transforms – Gabor, Wavelet Not many Architectures for Both – Current Day Applications like Handhelds, Mobile Phones, etc. require such DSP capabilities

Need for Reconfigurable Architecture n n n Multiple Orthogonal & Non-Orthogonal Transforms can be broken down to a basic set of Building blocks (DCT, DST, multipliers and Adders) Handheld devices don’t require much Multiprocessing – No need to waste hardware Increased Fault-Tolerance By Reconfiguration and Redundancy

AREA & POWER n INCREASING PROMINENCE OF PORTABLE SYSTEMS n n n Cell Phones Personal Digital Assistants Tablet PC’s BATTERY (40+ lbs) Need for Low Power & Area Battery Technology not kept pace with Semiconductor Technology

DISCRETE FOURIER TRANSFORM Traditional DFT Breakdown of 1 D DFT Breakdown of 2 D DFT APPLICATIONS: ®Image Processing ®Orthogonal Frequency Division Multiplexing

Discrete Gabor Transform and Coefficients Breakdown Applications n Speech Processing / Voice Recognition n Image Compression

Discrete Convolution Applications n Image Manipulation n Sound Processing

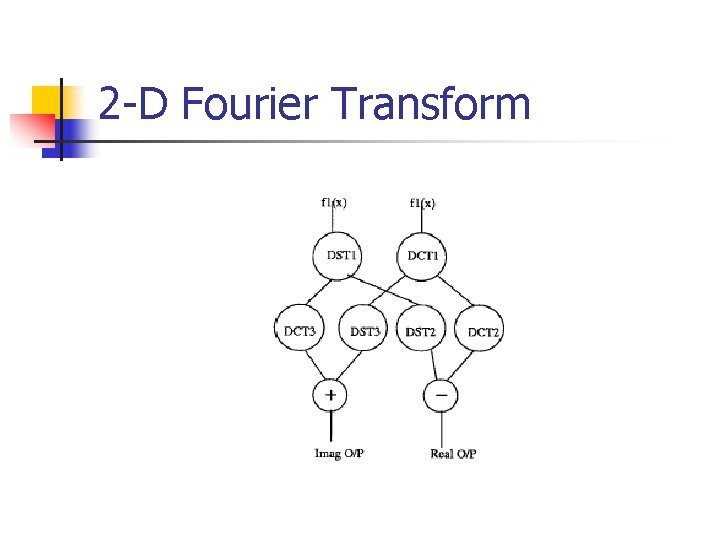
2 -D Fourier Transform

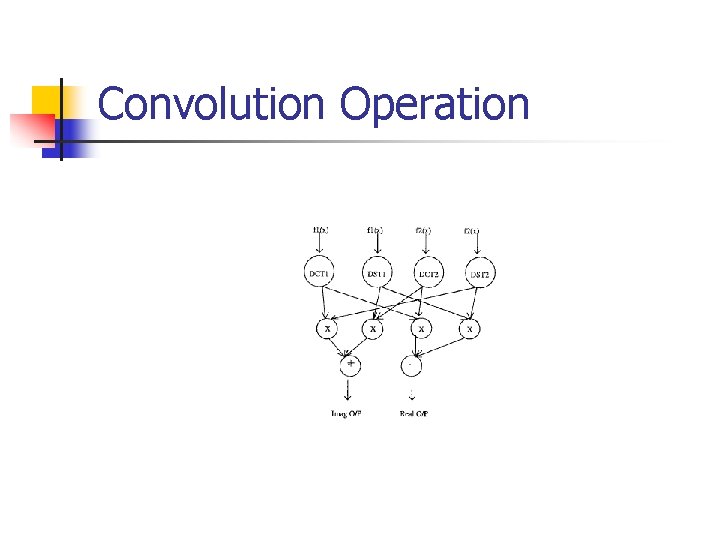
Convolution Operation

Convolution Operation (Contd. ) Computational complexity: 2 DCT, 2 DST, 4 real multiplications and 2 real additions

Imaginary Radix Representation n n A imaginary number system, Donald Knuth, Communications of the ACM Concept: a + ib = A – Interleave both real and Imaginary parts n n n # of multiplications get reduced to one Preserve Interleaving even during multiplication Requires slight modifications in multiplier design (one reason for migrating to FPGA)

Convolution Operation (using Complex Representation) Computational complexity: 2 DCT, 2 DST, 1 complex multiplication (same as real multiplication methodology)

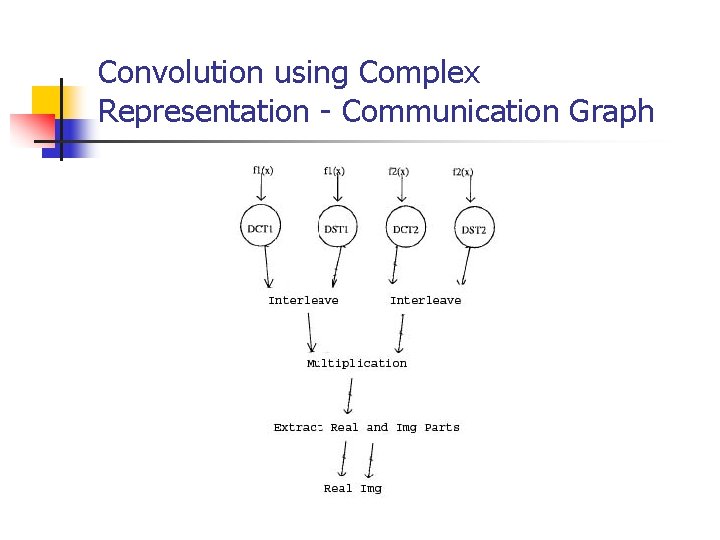
Convolution using Complex Representation - Communication Graph

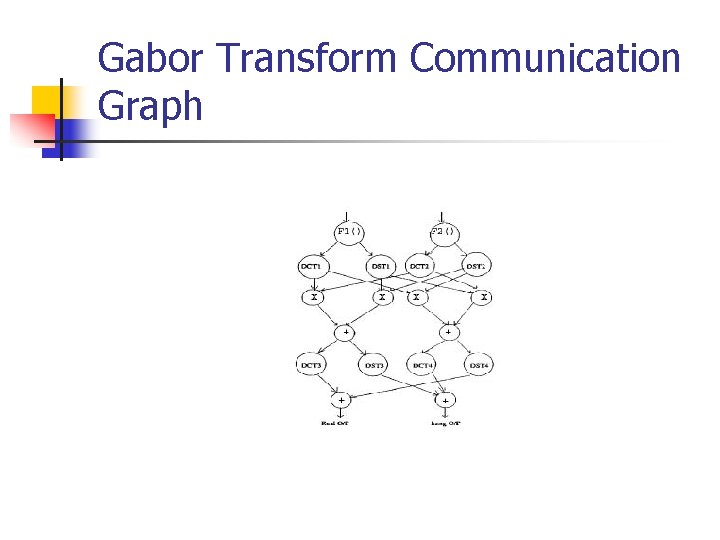
Gabor Transform Communication Graph

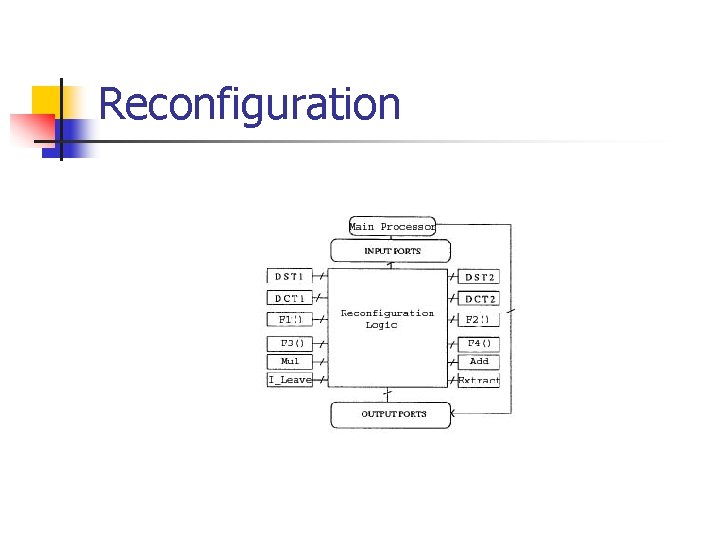
Reconfiguration

Work so far n Design & Synthesis of Basic Building Blocks n n n DCT DST Parallel Array Multiplier Reconfiguration Unit Partial Integration Work to be done: n n Complete Integration Functional Correctness Check

CONCLUSION Need for multiple transforms on same chip n n Mobile devices, Handhelds Not much multiprocessing required Use of Reconfigurable FPGA’s n Reduces n n AREA Increases n n Functionality Fault Tolerance