A Randomized Polynomial Time Simplex Algorithm for Linear

A Randomized Polynomial. Time Simplex Algorithm for Linear Programming by J. Kelner & D. Spielman Course: Advanced Algorithms CSG 713, Fall 2008 CCIS Department, Northeastern University Dimitrios Kanoulas

Linear Programming The form of the LP we will analyze: Maximize cx Subject to: Ax ≤ b where: Objective Function (c vector) Constraints x and c are two d-size vectors A is a nxd matrix b is a n-size right-hand vector Convex Polyhedron: Set of feasible points P: ={x|Ax ≤ b} where: the vertices can be defined by the d constraints Polytope: A bounded Convex Polyhedron

Opt. Simplex Method (Intuition) Starting from a vertex Try to find that vertex that optimizes the objective function TIME: (given random input constraints) • Worst-Case: Start exponential Thus: An algorithm that uses the Simplex method in worst-case polynomial time is needed. (open problem for 50 years) Solution: Randomization Picture from: commons. wikimedia. org

Main Result A Randomized Polynomial-Time LP Simplex Method Given a Linear Program, we can randomly perturb it, in such a way that: • We can use (Shadow) Simplex Method to solve this new nearby but different Linear Program and • The solution of this new Linear Program to be the solution of the starting one. and • It is polynomial in time w. h. p.

Overview of the Algorithm 1. Reduce the starting LP to a problem of certifying boundedness Boundedness does not depend on RHS vector b, of the constraints Loop: 2. Perturb randomly b vector of constraints and run shadow-vertex Simplex Method on perturbed polytope to generate certificate of boundedness 3. If it fails in constant number of steps, change the distribution on perturbations and run the algorithm again. TIME: The number of iterations of this loop is polynomial on the bit-length of the input, with high probability (w. h. p. )

Overview of the Algorithm 1. Reduce the starting LP to a problem of certifying boundedness A polyhedron is said to be bounded If the solution set is bounded The problem of determining whether a set of linear constraints defines an unbounded polyhedron or not. Boundedness does not depend on RHS vector b, of the constraints Maximize Subject to: cx Ax ≤ b

Overview of the Algorithm 1. Reduce the starting LP to a problem of certifying boundedness Boundedness does not depend on RHS vector b, of the constraints Loop: 2. Perturb randomly b vector of constraints and run shadow-vertex Simplex Method on perturbed polytope to generate certificate of boundedness 3. If it fails in constant number of steps, change the distribution on perturbations and run the algorithm again. TIME: The number of iterations of this loop is polynomial on the bit-length of the input, with high probability (w. h. p. )

Shadow of polytope The shadow of a polytope P onto a 2 -dimensions plane S is just the projection of P onto S. Create shadow: Every vertex/edge of the shadow’s polygon is the image of a vertex/edge of the polytope P The shadow is a polygon

Shadow of polytope The shadow of a polytope P onto a 2 -dimensions plane S is just the projection of P onto S. Idea: Find S such that the set of vertices of P that projects onto the boundary of the shadow polygon, are exactly the vertices of P that optimize the objective function in S. The shadow is a polygon

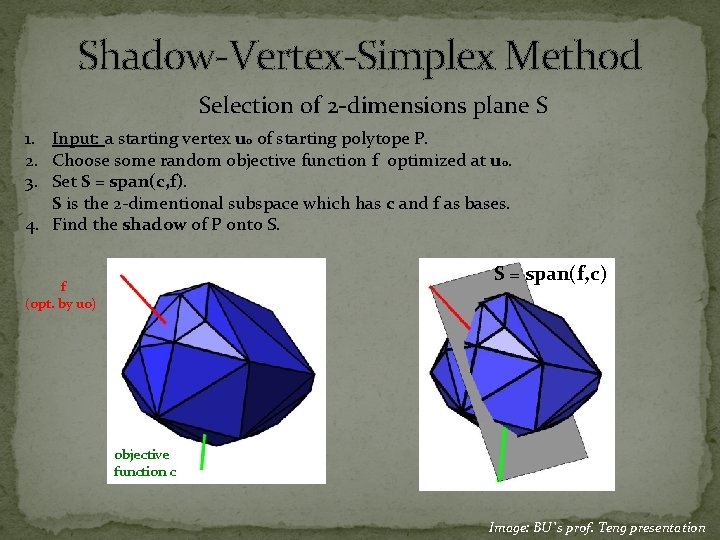
Shadow-Vertex-Simplex Method Selection of 2 -dimensions plane S 1. Input: a starting vertex u 0 of starting polytope P. 2. Choose some random objective function f optimized at u 0. 3. Set S = span(c, f). S is the 2 -dimentional subspace which has c and f as bases. 4. Find the shadow of P onto S. S = span(f, c) f (opt. by u 0) objective function c Image: BU`s prof. Teng presentation

Shadow-Vertex-Simplex Method 5. Each vertex y on P that projects onto the boundary of the shadow has a unique neighbor on P that projects onto the next vertex of the shadow in clockwise order. 6. Looking all the vertices on P that map to the boundary of the shadow we can move from vertex that optimize f to the vertex that optimize c. u 0 opt. f u opt. c or -c

Disadvantage of using the Starting LP Problem: By using the starting LP and the plane S we proposed, we cannot guarantee that: the number of edges of the shadow will be polynomial in size. [There is the possibility to be exponentially large] Solution: Guarantee that the number of edges of the shadow’s boundary will be polynomially large by perturbing the b-vector

Shadow Size (Number of shadow's edges) The real problem is to bound the number of shadow’s edges 2 cases: • Polytope in k-near-isotropic position • Polytope in non k-near-isotropic position

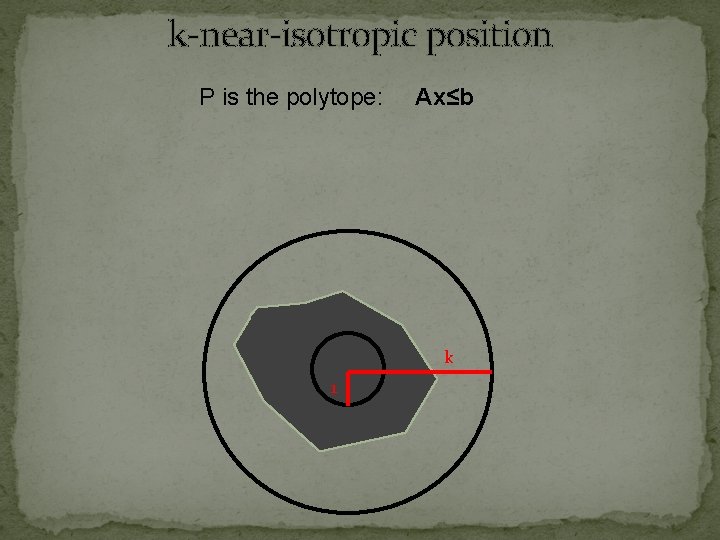
k-near-isotropic position P is the polytope: Ax≤b k 1

k-near-isotropic position Perturb polytope P: P : = {x | for each i: aix ≤ bi} Q : = {x | for each i: aix ≤ bi + ri} ri: independent exponentially distributed random variable with expectation λ ( Pr[ri≥t] = e-t/l, t≥ 0 ) Proof of Poly Size of the shadow • Upper bound of total shadow length (Shadow Size). • Lower bound expected length of each edge. Number of edges of the shadow is poly large w. h. p.

Until Now 1. Starting LP: Maximize cx Subject to: Ax ≤ b 2. Perturb b vector: guarantee that the number of edges of the shadow of the new polytope will be polynomially large w. h. p. 3. From the shadow find the vertex that optimizes the objective function c in polynomial number of steps, w. h. p.

Boundedness Certification Problem P is the polytope: Starting LP Ax≤b Boundedness Certification Problem Maximize c x Subject to: Ax ≤ b B w ≤ b’ B -> A, c, b Dual Reduction Dual LP Minimize b y Subject to: ATy = c y≥ 0 Combine Primal & Dual Need feasible x and y: Ax ≤ b AT y = c y≥ 0 cx=by

Boundedness Certification Problem Bw≤b Boundedness independent of b-vector Find certificate of boundedness by minimizing and maximizing the objective function (c)

Summary 1. Reduce the starting LP to a problem of certifying boundedness Boundedness does not depend on RHS vector b, of the constraints 2. We choose the correct 2 -dimensions plane S: care only about the boundary of the shadow 3. Perturb randomly b vector: guarantee that the number of edges of the boundary of the shadow is polynomially large, w. h. p. 4. We can move from a starting vertex of the shadow to this that optimizes c or -c objective function in polynomial number of steps, by doing fixed number of steps. 5. If it fails in constant number of steps, change the distribution on perturbations and run the algorithm again.

Thank You 11: 15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature. (From the movie: π) I have uploaded the presentation on my web site: http: //www. ccs. neu. edu/home/dkanou/