A QuantumStatisticalMechanical Extension of Gaussian Mixture Model Kazuyuki

  • Slides: 25
Download presentation
A Quantum-Statistical-Mechanical Extension of Gaussian Mixture Model Kazuyuki Tanaka Graduate School of Information Sciences,

A Quantum-Statistical-Mechanical Extension of Gaussian Mixture Model Kazuyuki Tanaka Graduate School of Information Sciences, Tohoku University, Sendai, Japan http: //www. smapip. is. tohoku. ac. jp/~kazu/ In collaboration with Koji Tsuda Max Planck Institute for Biological Cybernetics, 　Germany September 2007 IW-SMI 2007, Kyoto 1

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian Mixture Model 4. Quantum Belief Propagation 5. Concluding Remarks September 2007 IW-SMI 2007, Kyoto 2

Information Processing by using Quantum Statistical-Mechanics Quantum Annealing in Optimizations l Quantum Error Correcting

Information Processing by using Quantum Statistical-Mechanics Quantum Annealing in Optimizations l Quantum Error Correcting Codes etc. . . l Massive Information Processing by means of Density Matrix September 2007 IW-SMI 2007, Kyoto 3

Motivations How can we construct the quantum Gaussian mixture model? How can we construct

Motivations How can we construct the quantum Gaussian mixture model? How can we construct a dataclassification algorithm by using the quantum Gaussian mixture model? September 2007 IW-SMI 2007, Kyoto 4

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian Mixture Model 4. Quantum Belief Propagation 5. Concluding Remarks September 2007 IW-SMI 2007, Kyoto 5

Prior of Gauss Mixture Model One of three labels 1, 2 and 3 is

Prior of Gauss Mixture Model One of three labels 1, 2 and 3 is assigned to each node. 3 labels Label xi is generated randomly and independently of each node. Histogram 1 2 3 September 2007 xi =1 IW-SMI 2007, Kyoto xi =2 xi =3 6

Date Generating Process Data yi are generated randomly and independently of each node. xi

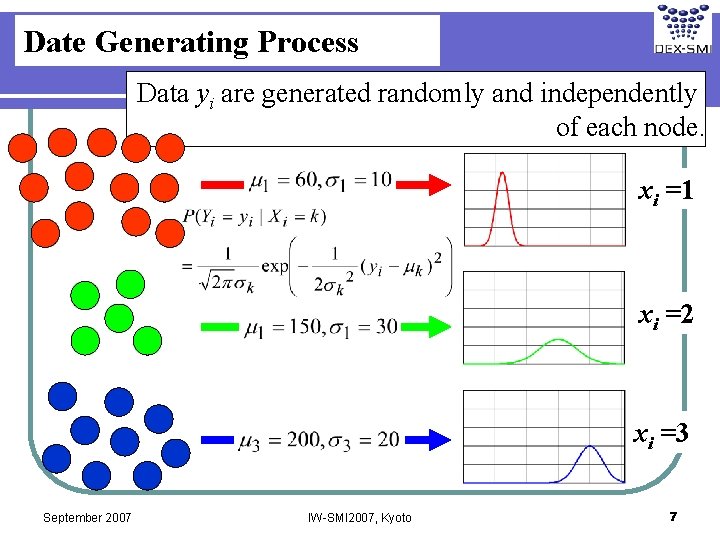
Date Generating Process Data yi are generated randomly and independently of each node. xi =1 xi =2 xi =3 September 2007 IW-SMI 2007, Kyoto 7

Gauss Mixture Models Prior Probability Data Generating Process Marginal Likelihood for Hyperparameters m, s

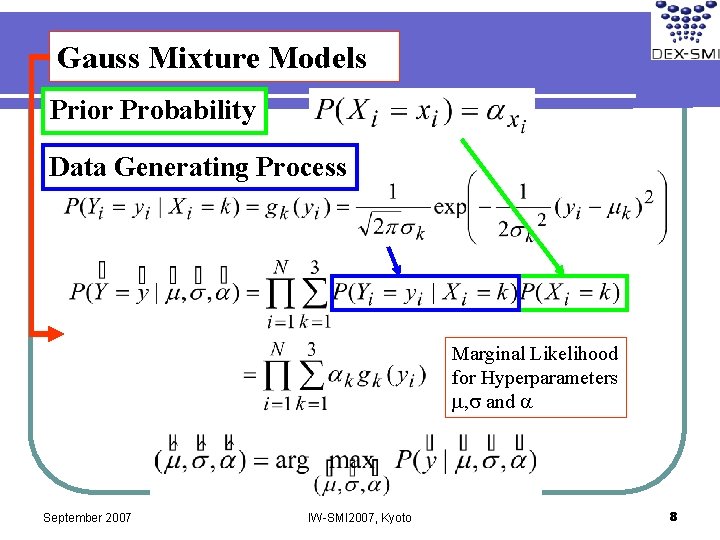
Gauss Mixture Models Prior Probability Data Generating Process Marginal Likelihood for Hyperparameters m, s and a September 2007 IW-SMI 2007, Kyoto 8

Conventional Gauss Mixture Models a, m, s r(yi) Labels September 2007 IW-SMI 2007, Kyoto

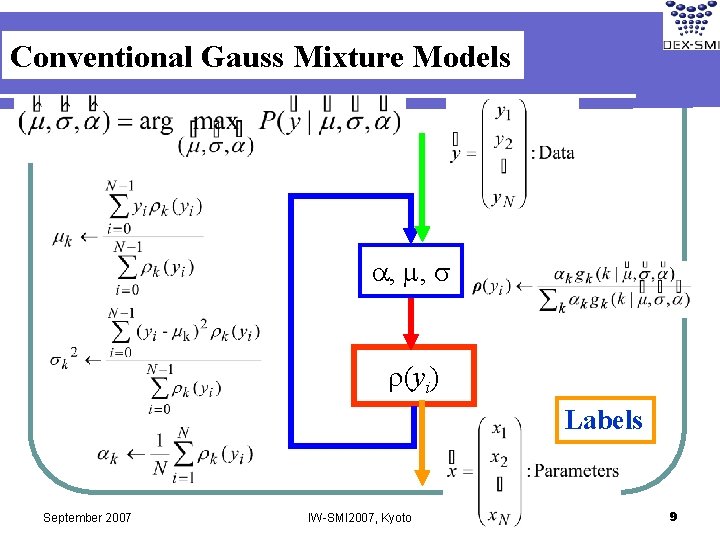
Conventional Gauss Mixture Models a, m, s r(yi) Labels September 2007 IW-SMI 2007, Kyoto 9

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian Mixture Model 4. Quantum Belief Propagation 5. Concluding Remarks September 2007 IW-SMI 2007, Kyoto 10

Quantum Gauss Mixture Models September 2007 IW-SMI 2007, Kyoto 11

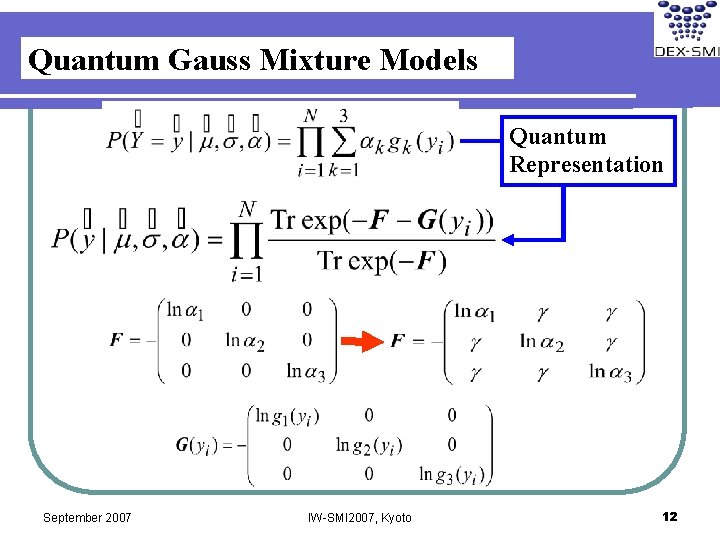
Quantum Gauss Mixture Models September 2007 IW-SMI 2007, Kyoto 11

Quantum Gauss Mixture Models Quantum Representation September 2007 IW-SMI 2007, Kyoto 12

Quantum Gauss Mixture Models Quantum Representation September 2007 IW-SMI 2007, Kyoto 12

Quantum Gauss Mixture Models September 2007 IW-SMI 2007, Kyoto 13

Quantum Gauss Mixture Models September 2007 IW-SMI 2007, Kyoto 13

Maxmum Likelihood Estimation in Quantum Gauss Mixture Model Linear Response Formulas September 2007 IW-SMI

Maxmum Likelihood Estimation in Quantum Gauss Mixture Model Linear Response Formulas September 2007 IW-SMI 2007, Kyoto 14

Quantum Gauss Mixture Models a, m, s r(yi) September 2007 IW-SMI 2007, Kyoto 15

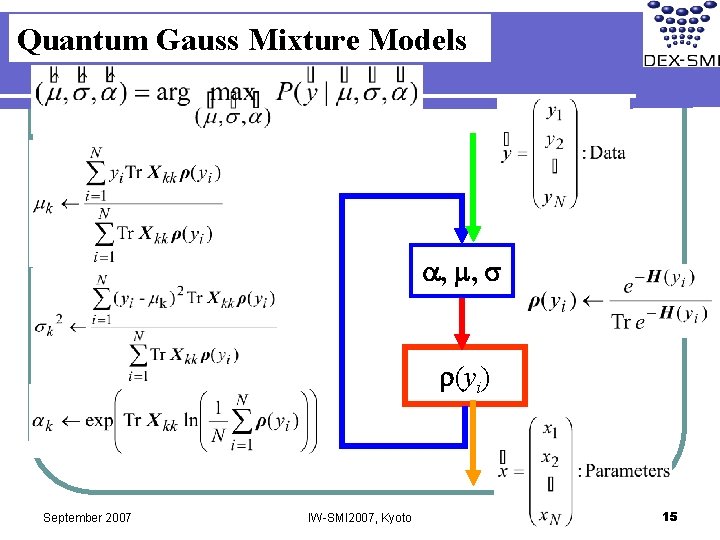
Quantum Gauss Mixture Models a, m, s r(yi) September 2007 IW-SMI 2007, Kyoto 15

Image Segmentation Original Image g = 0. 4 g = 0. 2 Conventional Gauss

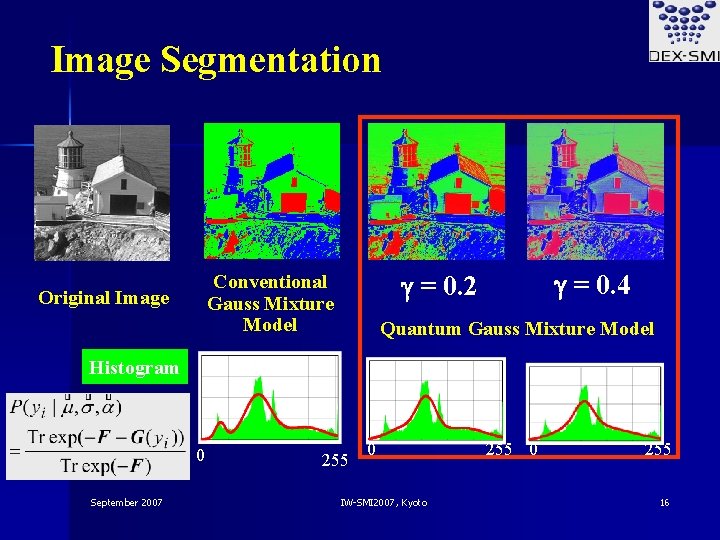
Image Segmentation Original Image g = 0. 4 g = 0. 2 Conventional Gauss Mixture Model Quantum Gauss Mixture Model Histogram 0 September 2007 255 0 IW-SMI 2007, Kyoto 255 0 255 16

Image Segmentation Original Image g = 1. 0 g = 0. 5 Conventional Gauss

Image Segmentation Original Image g = 1. 0 g = 0. 5 Conventional Gauss Mixture Model Quantum Gauss Mixture Model Histogram 0 September 2007 255 0 IW-SMI 2007, Kyoto 255 0 255 17

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian Mixture Model 4. Quantum Belief Propagation 5. Concluding Remarks September 2007 IW-SMI 2007, Kyoto 18

Image Segmentation by Combining Gauss Mixture Model with Potts Model 4 labels Potts Model

Image Segmentation by Combining Gauss Mixture Model with Potts Model 4 labels Potts Model Belief Propagation = September 2007 > IW-SMI 2007, Kyoto = 19

Image Segmentation Original Image Histogram Gauss Mixture Model and Potts Model Belief Propagation September

Image Segmentation Original Image Histogram Gauss Mixture Model and Potts Model Belief Propagation September 2007 IW-SMI 2007, Kyoto 20

Density Matrix and Reduced Density Matrix i September 2007 j Reducibility Condition IW-SMI 2007,

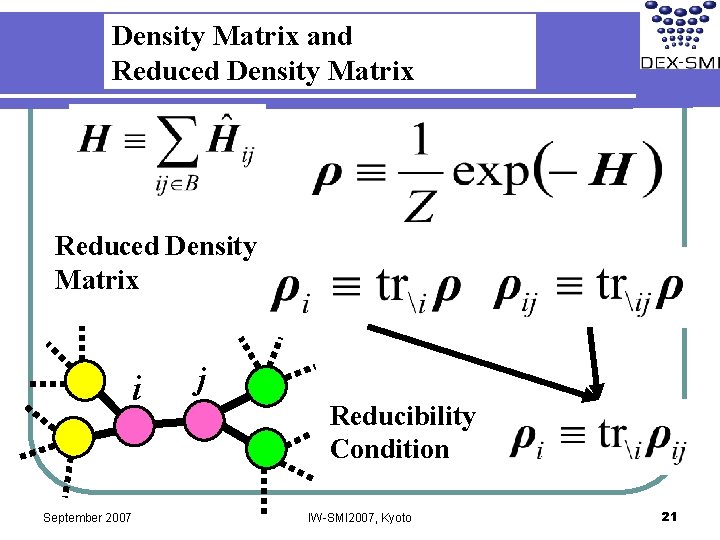
Density Matrix and Reduced Density Matrix i September 2007 j Reducibility Condition IW-SMI 2007, Kyoto 21

Reduced Density Matrix and Effective Fields i All effective field are matrices September 2007

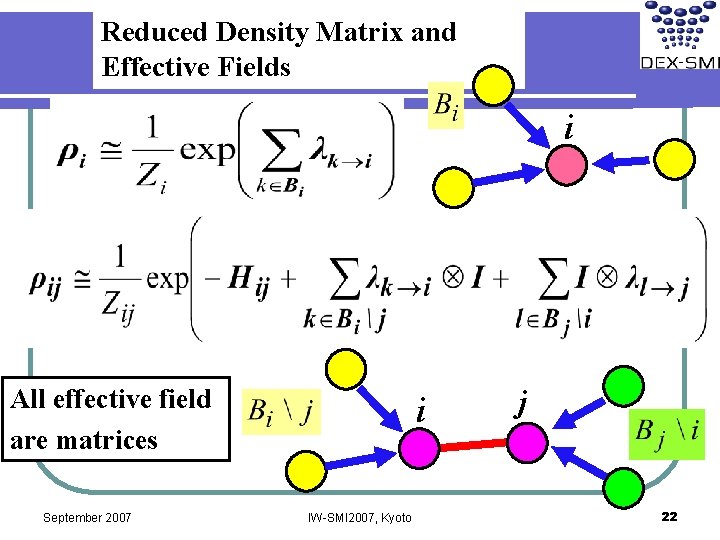
Reduced Density Matrix and Effective Fields i All effective field are matrices September 2007 i IW-SMI 2007, Kyoto j 22

Belief Propagation for Quantum Statistical Systems Propagating Rule of Effective Fields j i Output

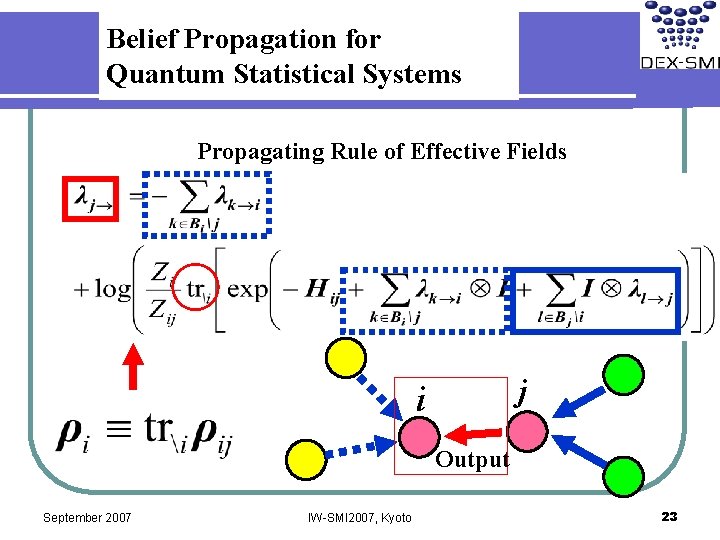
Belief Propagation for Quantum Statistical Systems Propagating Rule of Effective Fields j i Output September 2007 IW-SMI 2007, Kyoto 23

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian

Contents 1. Introduction 2. Conventional Gaussian Mixture Model 3. Quantum Mechanical Extension of Gaussian Mixture Model 4. Quantum Belief Propagation 5. Concluding Remarks September 2007 IW-SMI 2007, Kyoto 24

Summary An Extension to Quantum Statistical Mechanical Gaussian Mixture Model Practical Algorithm Linear Response

Summary An Extension to Quantum Statistical Mechanical Gaussian Mixture Model Practical Algorithm Linear Response Formula Future Problem Application of Potts Model and Quantum Belief Propagation Applications to Data Mining Extension to Quantum Deterministic Annealing September 2007 IW-SMI 2007, Kyoto 25