A Primer in Bifurcation Theory for Computational Cell

A Primer in Bifurcation Theory for Computational Cell Biologists Lecture 3: Hopf Bifurcation http: //www. biology. vt. edu/faculty/tyson/lectures. php John J. Tyson Click on icon to start audio Virginia Polytechnic Institute & Virginia Bioinformatics Institute

Signal-Response Curve = One-parameter Bifurcation Diagram • Saddle-Node (bistability, hysteresis) • Hopf Bifurcation (oscillations) • Subcritical Hopf • Cyclic Fold • Saddle-Loop • Saddle-Node Invariant Circle

Stability Analysis of Steady States and eigenvectors of the Jacobian matrix.

If det(J) = 0, then l = 0 is an eigenvalue, and the steady state is a saddle-node. p < p. SN p = p. SN det(J) = 0 p > p. SN

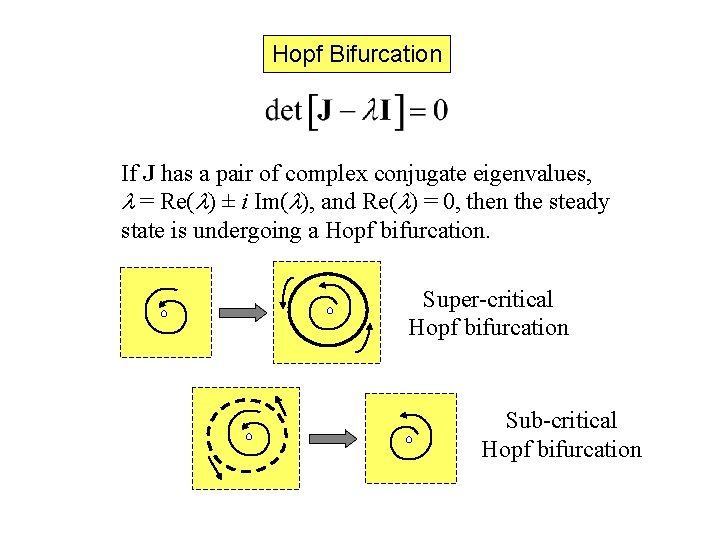
Hopf Bifurcation If J has a pair of complex conjugate eigenvalues, l = Re(l) ± i Im(l), and Re(l) = 0, then the steady state is undergoing a Hopf bifurcation. Super-critical Hopf bifurcation Sub-critical Hopf bifurcation

The Hopf Bifurcation Theorem. Suppose that at p = p. H the Jacobian matrix has a pair of complex conjugate eigenvalues, l = Re(l) ± i Im(l), with Re(l) = 0 and d. Re(l)/dp > 0. Then, for |p - p. H| sufficiently small, there exists a one-parameter family of small amplitude limit cycles for one of the following three conditions: (1) p > p. H, in which case the limit cycles are stable. (2) p < p. H, in which case the limit cycles are unstable. (3) p = p. H, in which case the limit cycles are neutral. Comments. Case (3) is unusual (‘structurally unstable’). In cases (1) and (2), the limit cycles are parameterized by the distance from the bifurcation point: |p - p. H|. The amplitude of the limit cycle grows like SQRT(|p – p. H|), and the period of the limit cycle is close to 2 p/Im(l).

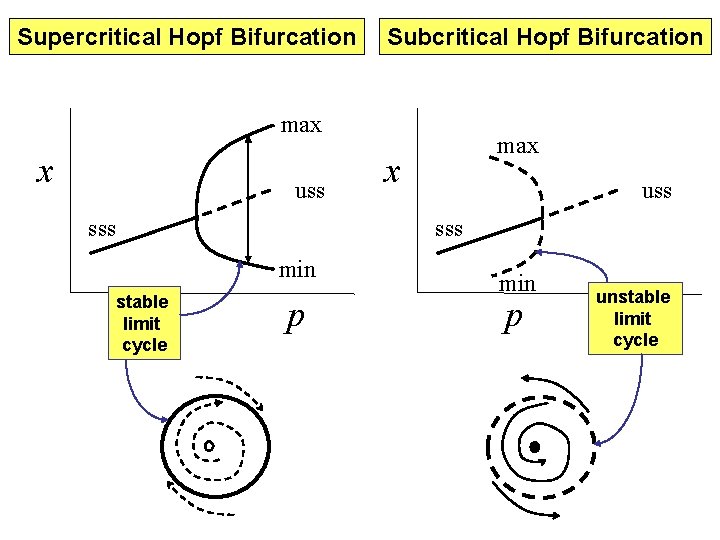
Supercritical Hopf Bifurcation Subcritical Hopf Bifurcation max x uss sss min stable limit cycle max p min p unstable limit cycle

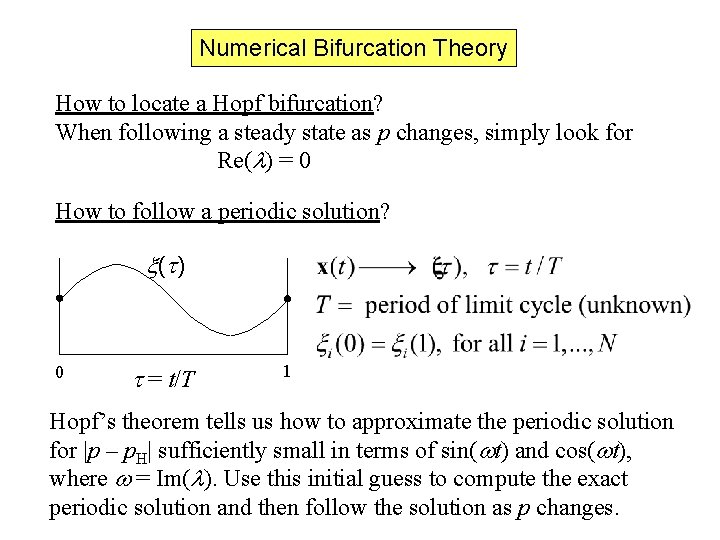
Numerical Bifurcation Theory How to locate a Hopf bifurcation? When following a steady state as p changes, simply look for Re(l) = 0 How to follow a periodic solution? x (t ) 0 t = t/T 1 Hopf’s theorem tells us how to approximate the periodic solution for |p – p. H| sufficiently small in terms of sin(wt) and cos(wt), where w = Im(l). Use this initial guess to compute the exact periodic solution and then follow the solution as p changes.

Stability of Periodic Solutions The stability of a periodic solution is determined by its “Floquet Multipliers”. Let P be a plane that is transverse to the periodic solution at a particular point: P Let y 0 = x(0)-x 0 be a small initial displacement in P from the periodic solution at x 0. Starting at y 0, integrate the ODEs forward in time until you return to P at point y 1 = x(T)-x 0. This procedure defines a nonlinear mapping yk+1 = Y(yk), which can be…

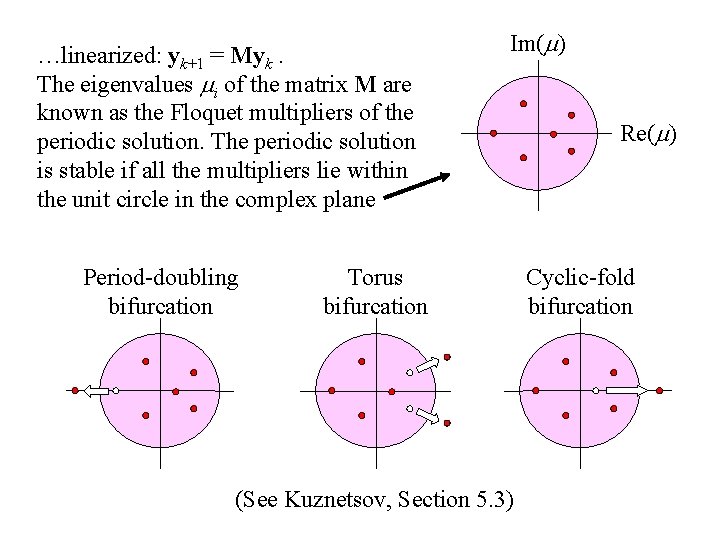
…linearized: yk+1 = Myk. The eigenvalues mi of the matrix M are known as the Floquet multipliers of the periodic solution. The periodic solution is stable if all the multipliers lie within the unit circle in the complex plane Period-doubling bifurcation Im(m) Torus bifurcation (See Kuznetsov, Section 5. 3) Re(m) Cyclic-fold bifurcation

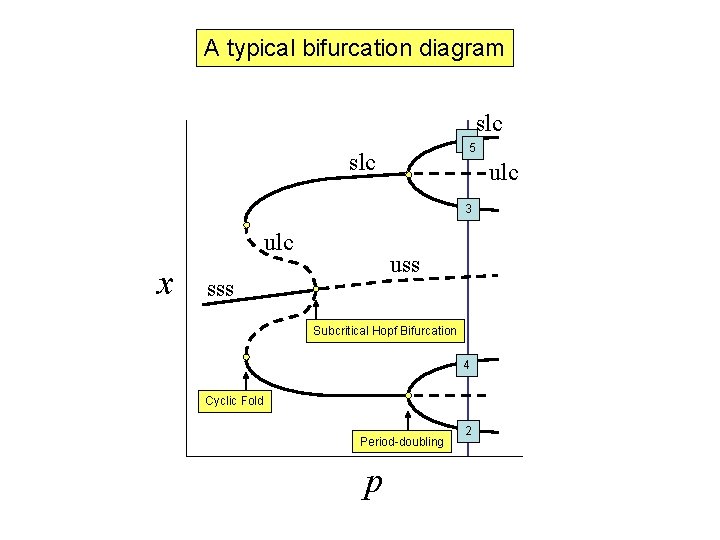
A typical bifurcation diagram 1 5 slc ulc 3 ulc x uss sss Subcritical Hopf Bifurcation 4 Cyclic Fold Period-doubling p slc 2

References • Strogatz, Nonlinear Dynamics and Chaos (Addison Wesley) • Kuznetsov, Elements of Applied Bifurcation Theory (Springer) • XPP-AUT www. math. pitt. edu/~bard/xpp • Oscill 8 http: //oscill 8. sourceforge. net