A Presentation on Cascadable Adiabatic Logic Circuits for

A Presentation on Cascadable Adiabatic Logic Circuits for Low-Power applications By Divya Yashwanth

What is an adiabatic circuit ? Adiabatic circuits are low power circuits which use "reversible logic" to conserve energy. The term comes from the fact that an adiabatic process is one in which the total heat or energy in the system remains constant. Most research has focused on building adiabatic logic out of CMOS. However, current CMOS technology, though fairly energy efficient compared to similar technologies, dissipate energy as heat, mostly when switching. Adiabatic circuits attempt to conserve charge by following two key rules: v. Never turn on a transistor when there is a voltage potential between the source and drain. v. Never turn off a transistor when current is flowing through it.

Adiabatic Logic circuits from CMOS transistors dissipate power when they switch. The main part of this dissipation is due to the need to charge and discharge the gate capacitance C through a component that has some resistivity R. The energy dissipated when charging of the gate is where T is the time it takes the gate to charge or discharge. In nonreversible circuits, the charging time T is proportional to RC. Reversible logic uses the fact that a single clock cycle is much longer then RC and thus attempts to spread the charging of the gate over the whole cycle and thus reduces the energy dissipated.

In order to extend the charging time of the gate never turn on a transistor that has a potential difference between source and drain, and furthermore, once the transistor is turned on, energy flows through it in a gradual and controlled manner. The second rule that adiabatic circuits must follow is never to turn off a transistor when there is current flowing through it because transistors are not perfect switches going from on to off instantly. Instead, it gradually changes from on to off when the gate voltage changes. Furthermore, the change is proportional to the speed at which the gate voltage changes. During this time, the voltage drop across the transistor greatly increases yet the resistance is not high enough to bring power dissipation to zero.

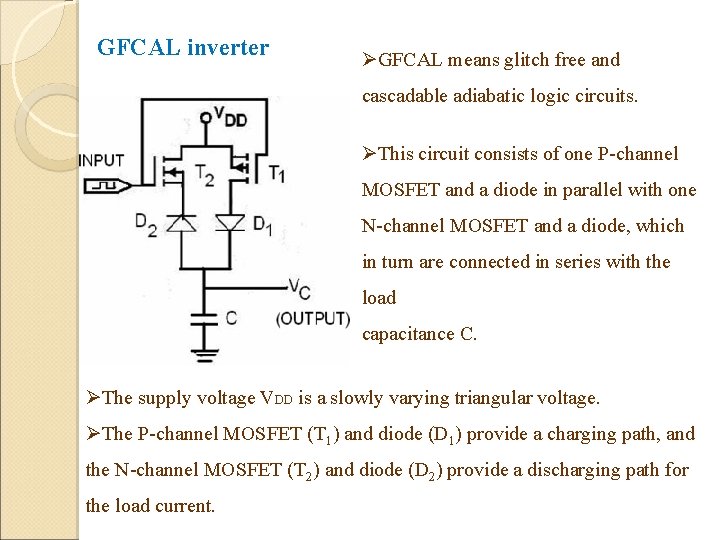
GFCAL inverter ØGFCAL means glitch free and cascadable adiabatic logic circuits. ØThis circuit consists of one P-channel MOSFET and a diode in parallel with one N-channel MOSFET and a diode, which in turn are connected in series with the load capacitance C. ØThe supply voltage VDD is a slowly varying triangular voltage. ØThe P-channel MOSFET (T 1) and diode (D 1) provide a charging path, and the N-channel MOSFET (T 2) and diode (D 2) provide a discharging path for the load current.

Operation of the circuit When the input is ‘ 0’ (logic ‘ 0’), T 1 is on and T 2 is off. Path T 1, D 1 allows the current flow from the supply and the capacitor becomes charged close to the peak value of VDD, producing logic ‘ 1’. The diode D 1 does not allow discharge into the supply when VDD is less than the output voltage. When the input is logic‘ 1’, T 2 is on and T 1 is off. The path D 2, T 2 starts conducting. The diode, D 2 prevents charging of the capacitor since it is reverse biased when VDD >VC and allows only discharging of the capacitor or pumping of energy back into the supply when VDD < VC. Thus, the capacitor voltage is brought down to a low value when the input is high irrespective of the previous output. Hence, the output is the complement of the input.

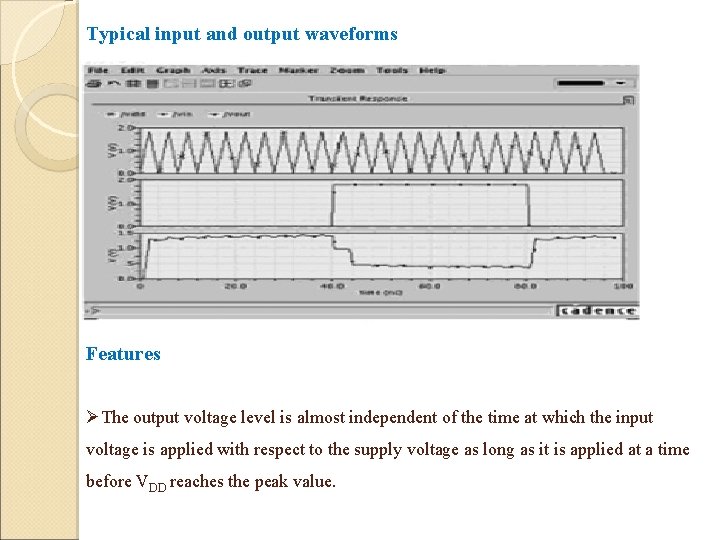
Typical input and output waveforms Features ØThe output voltage level is almost independent of the time at which the input voltage is applied with respect to the supply voltage as long as it is applied at a time before VDD reaches the peak value.

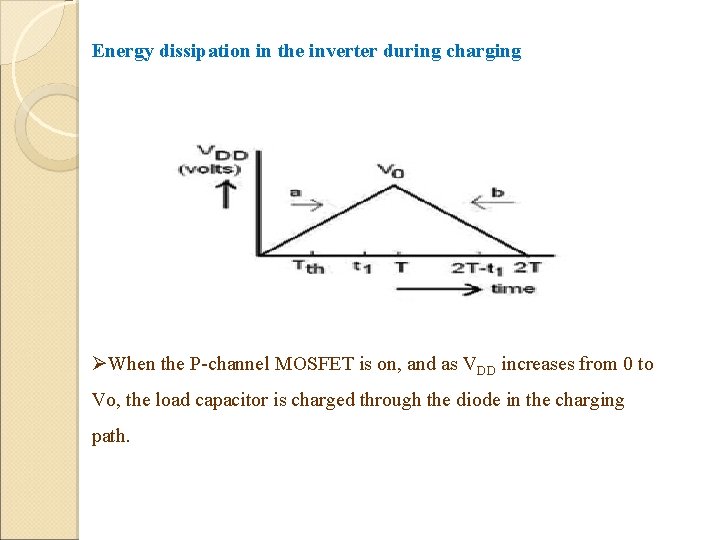
Energy dissipation in the inverter during charging ØWhen the P-channel MOSFET is on, and as VDD increases from 0 to Vo, the load capacitor is charged through the diode in the charging path.

The voltage reaches a peak value Vo in a time period T and its value VDD(t) at any time ‘t’ is when 0 ≤t ≤T when T ≤t ≤ 2 T The voltage VDD (t) reaches a value VB in a period Tth, when the diode starts conducting. Let Rch be the total resistance in the charging path. The voltage VC across the load capacitor ‘C’ for t> Tth, is Assuming that Tth > CRch, Energy Ech dissipated over the period 0 – T in the diode and the transistor is

Energy dissipation in the inverter during discharging When the N-channel MOSFET is on, the P-channel MOSFET is off, charging of the capacitor is prevented at the load and the capacitor discharges through the diode in the discharge path till t 1, that is, till VC is higher than the supply by at least VB, during the period when VDD increases from 0 to Vo. The capacitor then stops discharging at t 1 and again continues discharging from 2 T–t 1 until VC = VB. Let Rdis be the total resistance in the discharging path. Assuming CRdis < t 1, the energy Edc dissipated during discharging is the sum of energy dissipated during 0 to t 1 and (2 T–t 1 ) to 2 T which can be shown to be where

The total energy ED, dissipated during one cycle of charging and discharging is given by Where t 1 is given by Equation (1) From equation (1)the energy dissipated decreases as T increases. T indicates the rate at which the supply voltage varies and, hence, the energy dissipated decreases with slowly varying the supply voltages. The power dissipation generally changes with parameters like VO, the value of the capacitance, the equivalent series resistance because of the diode and the MOSFET.

Simulation of the inverter ØSimulated using Virtuoso Spectre circuit simulator of Cadence EDA tools. ØModels used for the simulation are BSIM 3 V 3 model parameters. ØLength of the transistor=180 nm, width of the transistor = 720 nm. ØLoad capacitance=30 f. F. ØSupply waveform is triangular with frequency=25 MHz and peak supply voltage=1. 8 V. ØInput signal is square wave with frequency=25 MHz. ØThe input logic ‘ 0’ value is 0. 45 V and input logic ‘ 1’ value is 1. 4 V. ØThe output logic values have been found to be 0. 45 and 1. 4 V corresponding to logic ‘ 0’ and logic ‘ 1’,

Comparison of theoretical and simulated values of energy dissipation for adiabatic inverter with CMOS inverter for input data ‘ 01’ at 25–MHZ Name of the circuit Energy dissipated Simulation results Theoretical values Adiabatic inverter 4. 04× 10 -14 4. 38× 10 -14 CMOS inverter 9. 12× 10 -14 9. 72× 10 -14 From the table, for both the cases, it is clear that in adiabatic inverter, the energy dissipation is only about 50% of that in the CMOS inverter.

Cascadability * The threshold voltage is 0. 6 V for the N-channel MOSFET and -0. 5 V for the P-channel MOSFET. * The peak value of voltage between gate and source (VGS) of the P-channel MOSFET is VGS =0. 45 -1. 8= -1. 35 V * When the input is logic ‘ 1’, the output does not go through charging of the capacitor. This feature enables this circuit to be used to drive the circuits, which follow without malfunctioning. These aspects have been verified by connecting two, three and four inverters in tandem. * A single power supply for all the inverters is used.

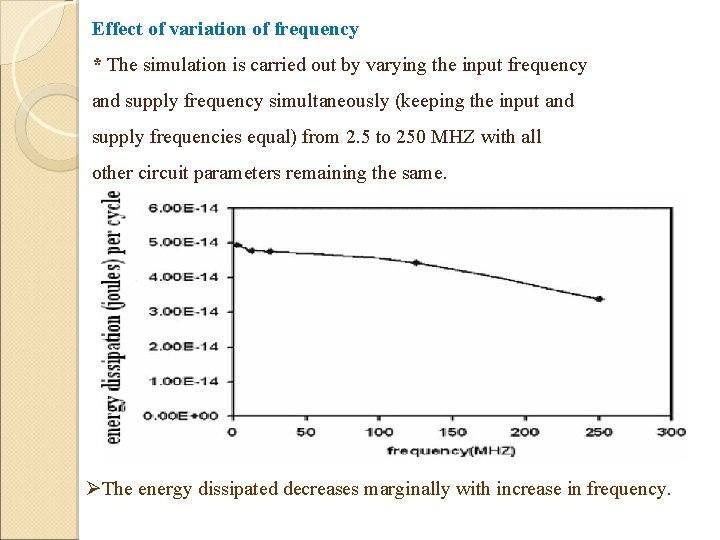
Effect of variation of frequency * The simulation is carried out by varying the input frequency and supply frequency simultaneously (keeping the input and supply frequencies equal) from 2. 5 to 250 MHZ with all other circuit parameters remaining the same. ØThe energy dissipated decreases marginally with increase in frequency.

ØThe output logic levels up to frequencies of 25 MHz are 1. 4 V corresponding to logic ‘ 1’ and 0. 45 V corresponding to logic ‘ 0’. ØAt frequencies higher than 25 MHz, the energy dissipated decreases gradually and the logic values vary from 1. 4 to 1. 35 V for logic ‘ 1’ and 0. 45 to 0. 47 V for logic ‘ 0’ at 250 MHz ØAt frequencies of 2. 50 GHz, the logic ‘ 1’ tends to a value of 0. 8 V and logic ‘ 0’ of – 0. 6 V. This is because the time period of the supply waveform is small compared with the time constant of charging and discharging, and the capacitor is unable to charge and discharge to the required levels. ØThe frequency of operation is increased by increasing the width of the transistors, which results in a decrease of the charging and discharging time constants but large W/L ratio results in higher power dissipation in both the CMOS and GFCAL circuits.

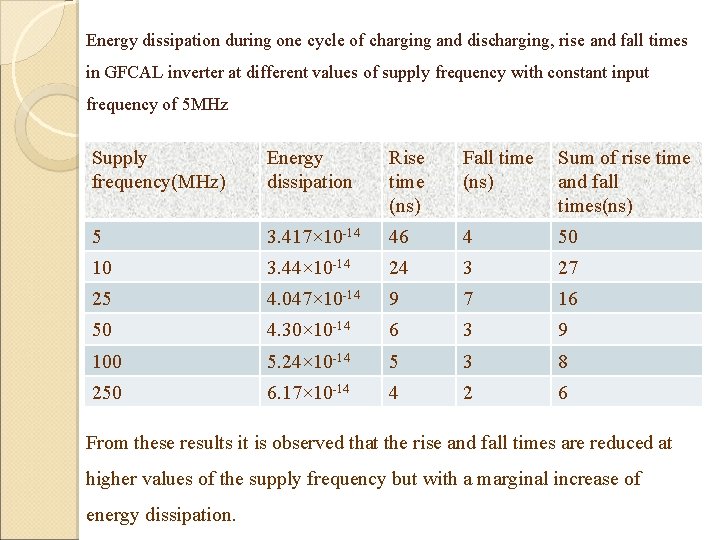
Energy dissipation during one cycle of charging and discharging, rise and fall times in GFCAL inverter at different values of supply frequency with constant input frequency of 5 MHz Supply frequency(MHz) Energy dissipation Rise time (ns) Fall time (ns) Sum of rise time and fall times(ns) 5 3. 417× 10 -14 46 4 50 10 3. 44× 10 -14 24 3 27 25 4. 047× 10 -14 9 7 16 50 4. 30× 10 -14 6 3 9 100 5. 24× 10 -14 5 3 8 250 6. 17× 10 -14 4 2 6 From these results it is observed that the rise and fall times are reduced at higher values of the supply frequency but with a marginal increase of energy dissipation.

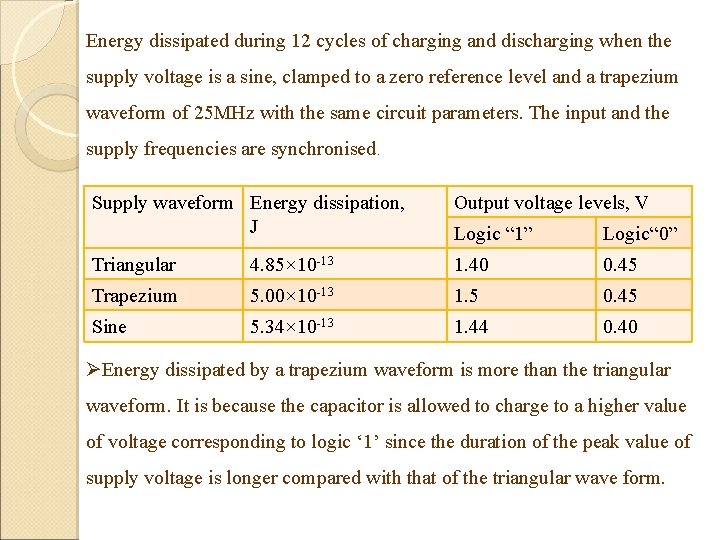
Energy dissipated during 12 cycles of charging and discharging when the supply voltage is a sine, clamped to a zero reference level and a trapezium waveform of 25 MHz with the same circuit parameters. The input and the supply frequencies are synchronised. Supply waveform Energy dissipation, J Output voltage levels, V Logic “ 1” Logic“ 0” Triangular 4. 85× 10 -13 1. 40 0. 45 Trapezium 5. 00× 10 -13 1. 5 0. 45 Sine 5. 34× 10 -13 1. 44 0. 40 ØEnergy dissipated by a trapezium waveform is more than the triangular waveform. It is because the capacitor is allowed to charge to a higher value of voltage corresponding to logic ‘ 1’ since the duration of the peak value of supply voltage is longer compared with that of the triangular wave form.

ØIn the case of the sine wave, the energy dissipation is more than that in the above cases because of the fast voltage rise near the zero crossing. Therefore triangular waveform is more suitable for less energy dissipation.

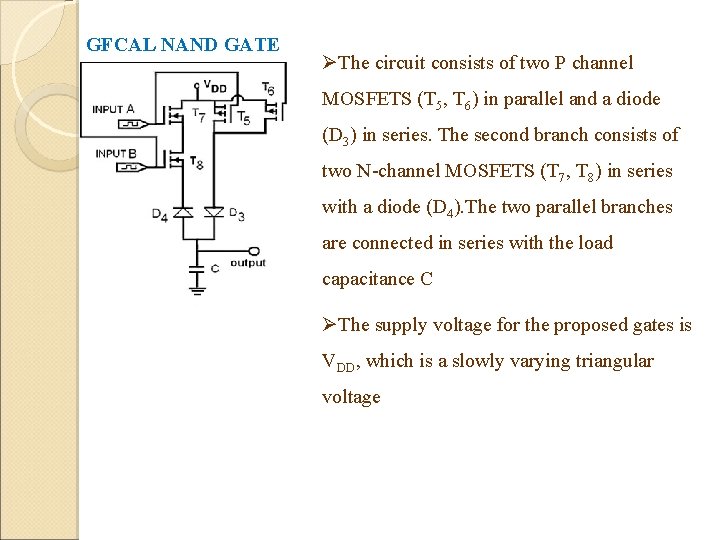
GFCAL NAND GATE ØThe circuit consists of two P channel MOSFETS (T 5, T 6) in parallel and a diode (D 3) in series. The second branch consists of two N-channel MOSFETS (T 7, T 8) in series with a diode (D 4). The two parallel branches are connected in series with the load capacitance C ØThe supply voltage for the proposed gates is VDD, which is a slowly varying triangular voltage

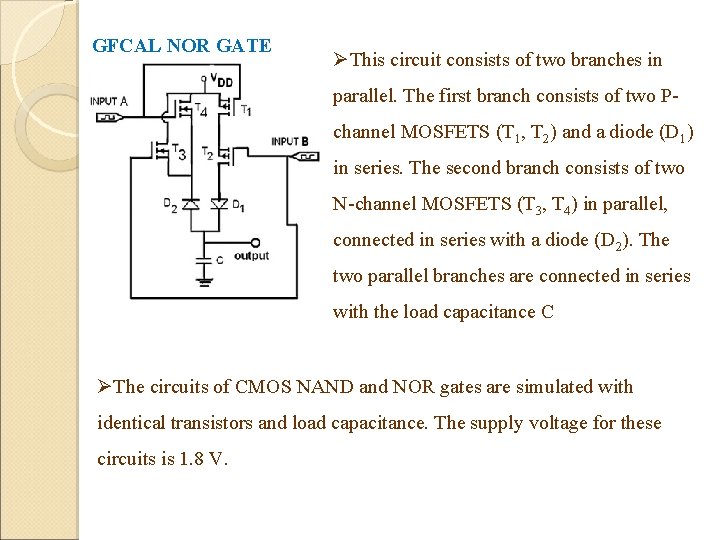
GFCAL NOR GATE ØThis circuit consists of two branches in parallel. The first branch consists of two Pchannel MOSFETS (T 1, T 2) and a diode (D 1) in series. The second branch consists of two N-channel MOSFETS (T 3, T 4) in parallel, connected in series with a diode (D 2). The two parallel branches are connected in series with the load capacitance C ØThe circuits of CMOS NAND and NOR gates are simulated with identical transistors and load capacitance. The supply voltage for these circuits is 1. 8 V.

Comparison of simulated values of energy dissipation for the GFCAL NOR and NAND gates corresponding to input strings A =101010101010 and B = ‘ 101010101010’ for one cycle of charging and discharging at 25 MHz. Name of the circuit Energy dissipated, J Proposed GFCAL CMOS NAND gate 4. 88× 10 -14 1. 15× 10 -13 NOR gate 4. 94× 10 -14 1. 180× 10 -13 From the table, for both the cases, it is clear that in adiabatic gates, the energy dissipation is only about 50% of that in the CMOS gates.

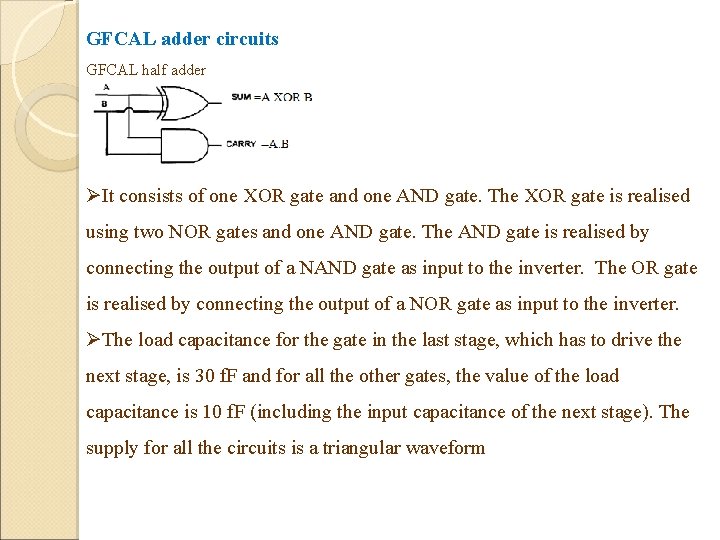
GFCAL adder circuits GFCAL half adder ØIt consists of one XOR gate and one AND gate. The XOR gate is realised using two NOR gates and one AND gate. The AND gate is realised by connecting the output of a NAND gate as input to the inverter. The OR gate is realised by connecting the output of a NOR gate as input to the inverter. ØThe load capacitance for the gate in the last stage, which has to drive the next stage, is 30 f. F and for all the other gates, the value of the load capacitance is 10 f. F (including the input capacitance of the next stage). The supply for all the circuits is a triangular waveform

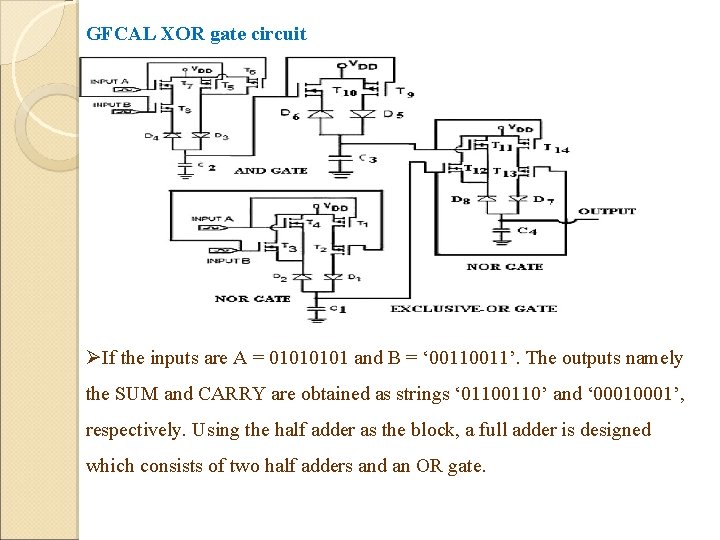
GFCAL XOR gate circuit ØIf the inputs are A = 0101 and B = ‘ 0011’. The outputs namely the SUM and CARRY are obtained as strings ‘ 0110’ and ‘ 0001’, respectively. Using the half adder as the block, a full adder is designed which consists of two half adders and an OR gate.

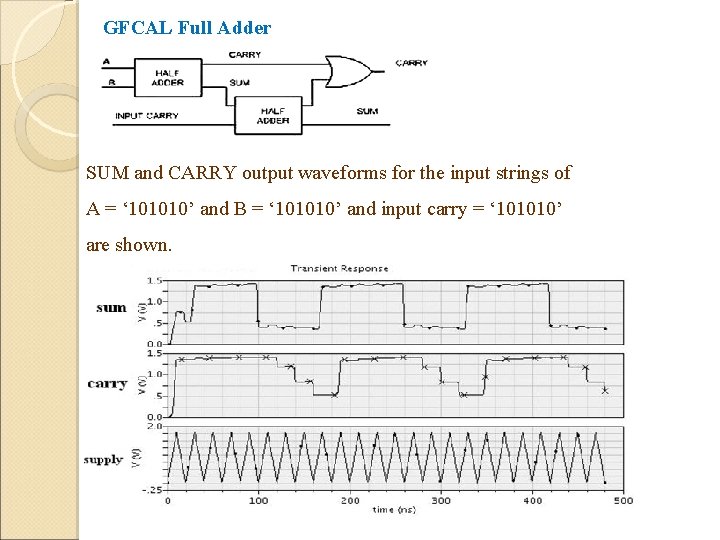
GFCAL Full Adder SUM and CARRY output waveforms for the input strings of A = ‘ 101010’ and B = ‘ 101010’ and input carry = ‘ 101010’ are shown.

GFCAL 4 bit Ripple Carry Adder ØIt consists of four full adders and the carry output is given as the carry input to the following adder. ØThe functionality of the circuit is guaranteed by maintaining the supply frequency higher than the frequency of the input data.

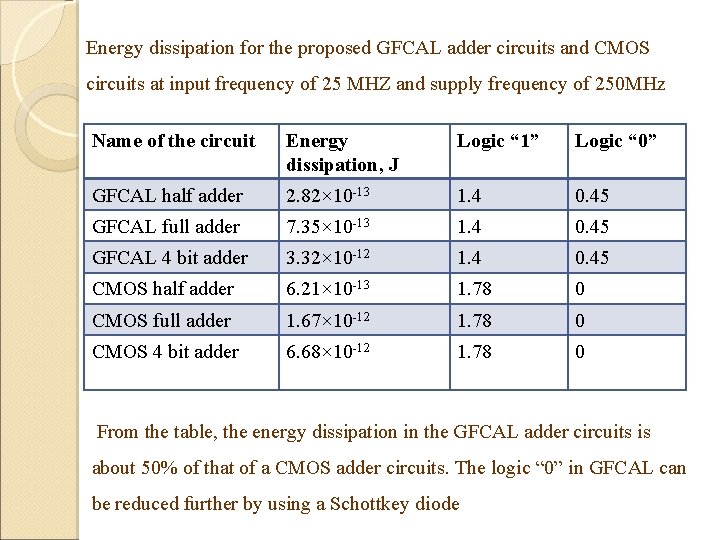
Energy dissipation for the proposed GFCAL adder circuits and CMOS circuits at input frequency of 25 MHZ and supply frequency of 250 MHz Name of the circuit Energy dissipation, J Logic “ 1” Logic “ 0” GFCAL half adder 2. 82× 10 -13 1. 4 0. 45 GFCAL full adder 7. 35× 10 -13 1. 4 0. 45 GFCAL 4 bit adder 3. 32× 10 -12 1. 4 0. 45 CMOS half adder 6. 21× 10 -13 1. 78 0 CMOS full adder 1. 67× 10 -12 1. 78 0 CMOS 4 bit adder 6. 68× 10 -12 1. 78 0 From the table, the energy dissipation in the GFCAL adder circuits is about 50% of that of a CMOS adder circuits. The logic “ 0” in GFCAL can be reduced further by using a Schottkey diode

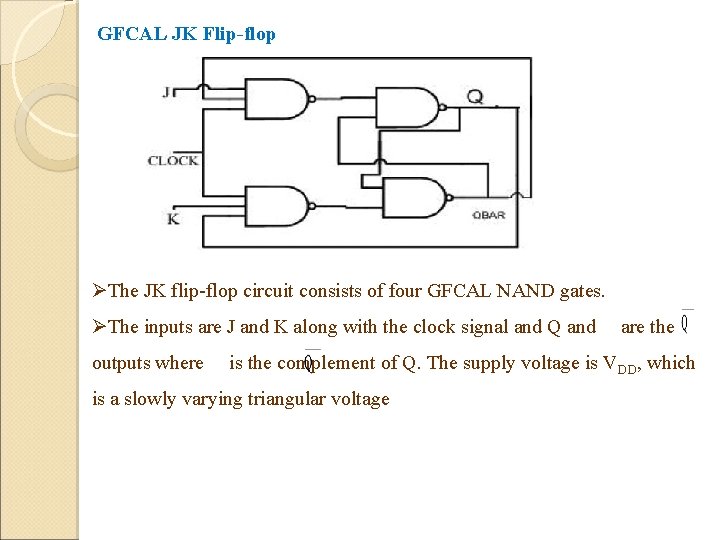
GFCAL JK Flip-flop ØThe JK flip-flop circuit consists of four GFCAL NAND gates. ØThe inputs are J and K along with the clock signal and Q and outputs where are the is the complement of Q. The supply voltage is VDD, which is a slowly varying triangular voltage

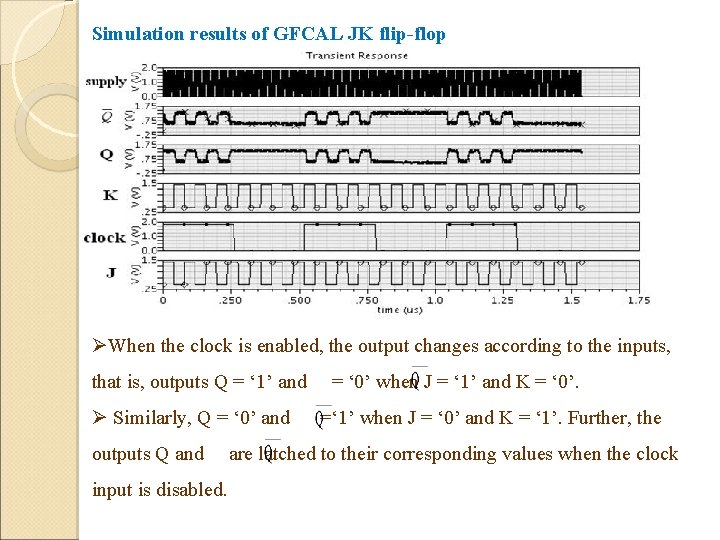
Simulation results of GFCAL JK flip-flop ØWhen the clock is enabled, the output changes according to the inputs, that is, outputs Q = ‘ 1’ and Ø Similarly, Q = ‘ 0’ and outputs Q and input is disabled. = ‘ 0’ when J = ‘ 1’ and K = ‘ 0’. =‘ 1’ when J = ‘ 0’ and K = ‘ 1’. Further, the are latched to their corresponding values when the clock

Energy dissipation for the proposed GFCAL JK Flip-flop and CMOS circuits at input frequency of 25 MHZ and supply frequency of 250 MHz Name of the circuit Energy dissipation, J Logic “ 1” Logic “ 0” GFCAL JK Flipflop 1. 28× 10 -13 1. 4 0. 45 1. 78 0 CMOS JK Flip-flop 2. 87× 10 -13 From the table, the energy dissipation in the GFCAL JK Flip-flop is about 50% of that of a CMOS JK Flip flop circuits.

Comparison of proposed GFCAL family with other adiabatic logic families Given the length and width of a transistor are 180 nm and 720 nm, respectively, and the value of load capacitance is 30 f. F. The input frequency is same as the supply frequency (25 MHZ). ØA 2 N-2 N 2 D inverter uses four transistors and two-diodes. The capacitor has to be charged first before evaluating the outputs, which may cause unwanted switching activities at the output nodes. Ø A 2 N-2 P inverter uses four-transistors and a 2 N-2 N 2 P inverter uses sixtransistors. A PAL inverter uses four-transistors but requires two complementary sinusoidal power clocks in cascaded circuits.

* A CAL inverter contains eight-transistors and needs a single clock and two additional timing control clocks for correct operation. * A True single phase energy recovery logic (TSEL) inverter contains six- transistors and needs a single clock, but it has discharge /charge and evaluation phases, which may cause unnecessary switching activities at nodes in hierarchical circuits. * A Quasi-static energy recovery logic (QSERL) inverter contains four transistors and needs a single clock, but a threshold voltage drop at MOSFETS used as diodes will occur and also the capacitance effect exists at higher frequencies. * An ADL inverter contains one-transistor and one diode along with a load capacitor and needs a four-phase clock in cascaded circuits. Since the capacitor has to be pre-charged, unwanted switching activity may occur at the output nodes.

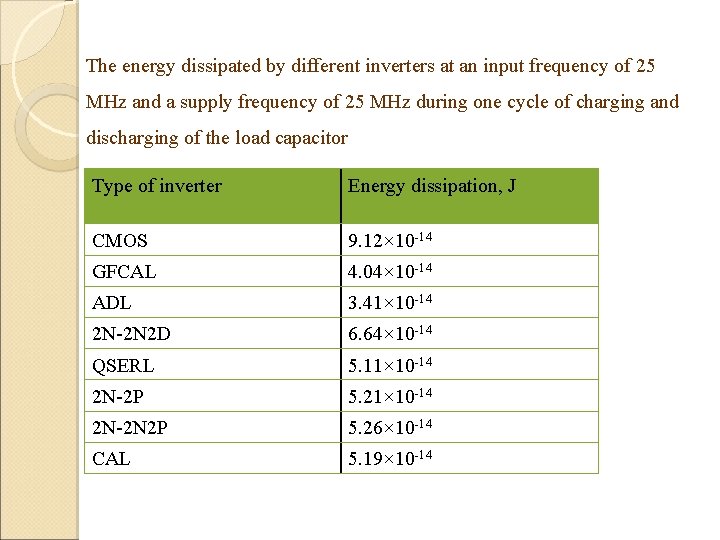
The energy dissipated by different inverters at an input frequency of 25 MHz and a supply frequency of 25 MHz during one cycle of charging and discharging of the load capacitor Type of inverter Energy dissipation, J CMOS 9. 12× 10 -14 GFCAL 4. 04× 10 -14 ADL 3. 41× 10 -14 2 N-2 N 2 D 6. 64× 10 -14 QSERL 5. 11× 10 -14 2 N-2 P 5. 21× 10 -14 2 N-2 N 2 P 5. 26× 10 -14 CAL 5. 19× 10 -14

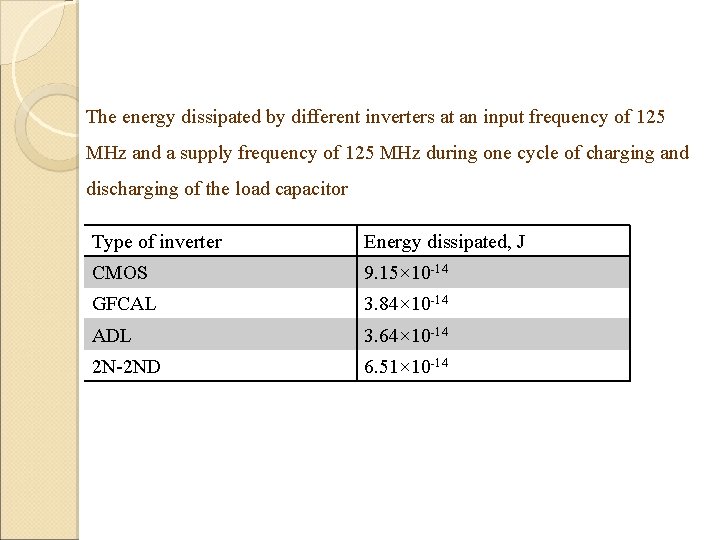
The energy dissipated by different inverters at an input frequency of 125 MHz and a supply frequency of 125 MHz during one cycle of charging and discharging of the load capacitor Type of inverter Energy dissipated, J CMOS 9. 15× 10 -14 GFCAL 3. 84× 10 -14 ADL 3. 64× 10 -14 2 N-2 ND 6. 51× 10 -14

CONCLUSIONS 1. In Cascadable adiabatic circuits the energy saved is more than 50% compared with that of conventional CMOS circuits. 2. This circuit can be used in building hierarchical circuits as the input and output logic levels are the same, just like in the case of conventional digital circuits, and there are no glitches. 3. All the circuits can be operated with a single power supply and there is no need of a complementary input. It has been shown that GFCAL circuits can work well up to 250 MHZ using 0. 18 μm with a reasonable W/L ratio of the transistors. 4. The number of transistors in CMOS and adiabatic circuit are the same, except that one diode per branch is extra in adiabatic circuit. Thus, the circuits can be easily cascaded.

5. Power saving in these circuits is because of (i) The supply voltage is a slowly varying voltage, which results in energy saving during charging and discharging. (ii) The energy stored in the load capacitor is pumped back into the supply to realise a transition from logic ‘ 1’ to logic ‘ 0’. (iii) There is no short circuit current from the supply to the ground at any time during the transition of logic ‘ 1’ to logic ‘ 0’ or logic ‘ 0’ to logic ‘ 1’ unlike in the CMOS circuits. (iv) The diode in the discharge path of the gate prevents the flow of current spikes from the input data into the load capacitor.

REFERENCES 1. Cascadable adiabatic logic circuits for low-power applications N. S. S. Reddy, M. Satyam, K. L. Kishore, IET Circuits, Devices and Systems November 2008, Volume 2, No. 6, Pages 518 -526. 2. Adiabatic Logic by Benjamin Gojman, August 8, 2004 http: //www. cs. caltech. edu/cbsss/finalreport/nanoscale_ind_gojman. pdf 3. ‘Second-order adiabatic computation with 2 N-2 P and 2 N-2 P logic circuits’ by Kramer A, Denker J. S. , Flower B, Moroney J, Proc. Intern. Symposium on Low Power Design, 1995, pp. 191– 196