A Presentation on APPLIED MATHEMATICS 9018 Subject Title

A Presentation on APPLIED MATHEMATICS (9018)

Subject Title : Applied Mathematics Course Name: Second Year Engineering Diploma Course Code : CE/CH/ME Semester : Third Subject Abbr : AMT Subject Code : 9018 2
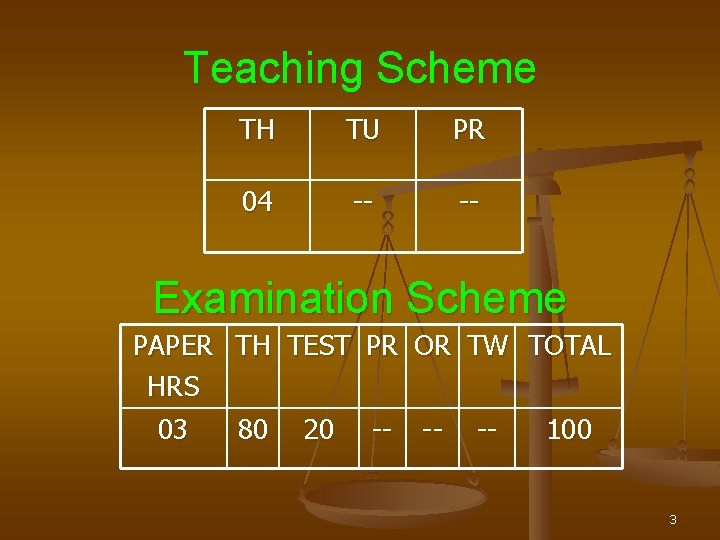
Teaching Scheme TH TU PR 04 -- -- Examination Scheme PAPER TH TEST PR OR TW TOTAL HRS 03 80 20 -- -- -- 100 3

Rationale Since 21 st century man has developed new disciplines like Information technology , Genetic engineering , Biotechnology etc. on the basis of Mathematics. Thus the study of this subject is necessary to develop the skills essential for these new disciplines in the student. The study of mathematics is necessary to develop in the student the skills essential for studying new technological development. This subject introduces some applications of engineering, through which the student can understand the link of Mathematics with engineering principles. 4

Objectives The students will be able to: n n Apply Mathematical term, concept, principles and different methods for studying engineering subjects Apply Mathematical methods to solve technical problems, Execute management plans with precision. Use Mathematical techniques necessary for daily and practical problems. 5
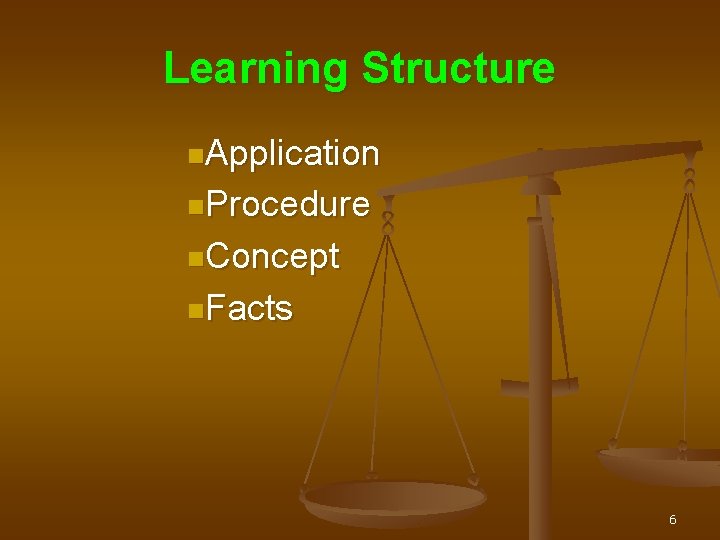
Learning Structure n. Application n. Procedure n. Concept n. Facts 6

Application: - n Apply the principles of Mathematics to solve problems in Civil and Mechanical Field 7

Procedure n n Methods of finding integration definite integration and its properties. Methods of solving differential equation of first order and first degree. Use of Binomial, Normal and Poission distributions for solving different examples. Methods for finding approximate roots by using bisection, Regula-falsi, Newton-Raphson method, Gauss elimination method, Jacobi and Gauss-seidal methods 8

Concept n n Integration of standard functions. Rules of integration. Integration by parts, partial fractions. Order, degree of differential equation Probability of repeated trials of random experiment. Higher order algebraic equations. Upper and lower triangular matrix, iterative methods. 9

Facts n n n n First order differentiation. Definition of integration as anti derivative. Integration. Definition of differential equation. Permutation and combination. Probability of an event. Relation between degree of equation and roots. Relation between no. of unknowns and equations. 10
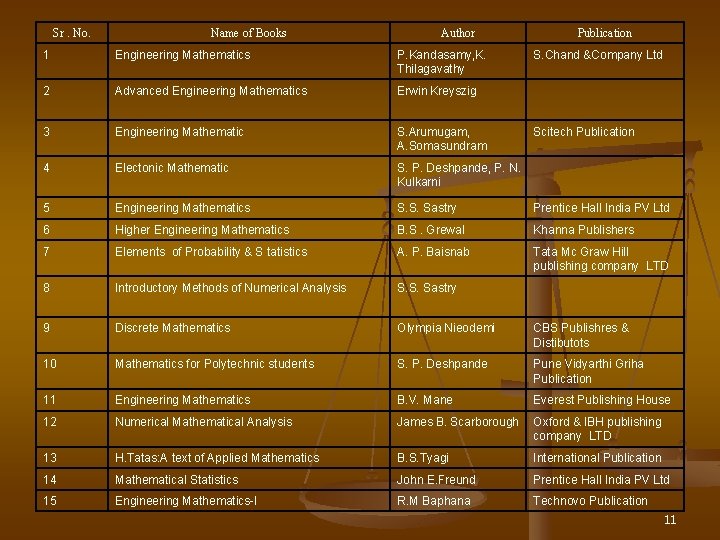
Sr. No. Name of Books Author Publication 1 Engineering Mathematics P. Kandasamy, K. Thilagavathy S. Chand &Company Ltd 2 Advanced Engineering Mathematics Erwin Kreyszig 3 Engineering Mathematic S. Arumugam, A. Somasundram 4 Electonic Mathematic S. P. Deshpande, P. N. Kulkarni 5 Engineering Mathematics S. S. Sastry Prentice Hall India PV Ltd 6 Higher Engineering Mathematics B. S. Grewal Khanna Publishers 7 Elements of Probability & S tatistics A. P. Baisnab Tata Mc Graw Hill publishing company LTD 8 Introductory Methods of Numerical Analysis S. S. Sastry 9 Discrete Mathematics Olympia Nieodemi CBS Publishres & Distibutots 10 Mathematics for Polytechnic students S. P. Deshpande Pune Vidyarthi Griha Publication 11 Engineering Mathematics B. V. Mane Everest Publishing House 12 Numerical Mathematical Analysis James B. Scarborough Oxford & IBH publishing company LTD 13 H. Tatas: A text of Applied Mathematics B. S. Tyagi International Publication 14 Mathematical Statistics John E. Freund Prentice Hall India PV Ltd 15 Engineering Mathematics-I R. M Baphana Technovo Publication Scitech Publication 11
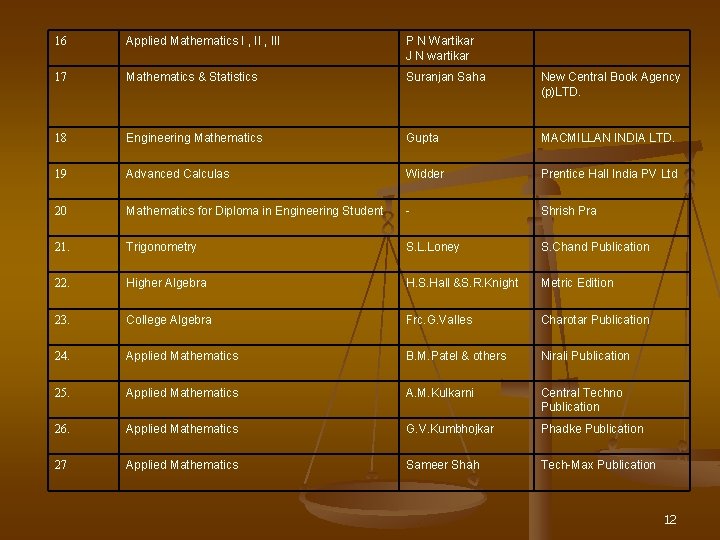
16 Applied Mathematics I , III P N Wartikar J N wartikar 17 Mathematics & Statistics Suranjan Saha New Central Book Agency (p)LTD. 18 Engineering Mathematics Gupta MACMILLAN INDIA LTD. 19 Advanced Calculas Widder Prentice Hall India PV Ltd 20 Mathematics for Diploma in Engineering Student - Shrish Pra 21. Trigonometry S. L. Loney S. Chand Publication 22. Higher Algebra H. S. Hall &S. R. Knight Metric Edition 23. College Algebra Frc. G. Valles Charotar Publication 24. Applied Mathematics B. M. Patel & others Nirali Publication 25. Applied Mathematics A. M. Kulkarni Central Techno Publication 26. Applied Mathematics G. V. Kumbhojkar Phadke Publication 27 Applied Mathematics Sameer Shah Tech-Max Publication 12

For Theory 80 marks MSBTE conducting examination at end of semester MSBTE Question Paper Format 9018 0910 -I 3 Hours / 80 Marks Seat No. Instructions(1)All Questions are compulsory. (2)Answer each next main Question on a new page. (3)Figures to the right indicate full marks. (4)Assume suitable data, if necessary. (5)Use of Non-programmable Electronic Pocket Calculator is permissible. 13

Q 1. Attempt any EIGHT of the following a) Integration b) Integration c) Integration d) Integration e) Definite Integration f) Differential equations g) Differential equations h) Application of Integration i) Probability Distribution j) Probability Distribution [ marks 16 ] 14
![Q 2. Attempt any Three of the following [ marks 12] a) Integration b) Q 2. Attempt any Three of the following [ marks 12] a) Integration b)](http://slidetodoc.com/presentation_image_h2/67569e9c1dd829ca660e8a31751cb165/image-15.jpg)
Q 2. Attempt any Three of the following [ marks 12] a) Integration b) Integration c) Definite Integration d) Application of Integration Q 3. Attempt any Three of the following [ marks 12 ] a) Definite Integration b) Application of Integration c) Application of Integration d) Application of Integration 15

Q 4. Attempt any Three of the following a) b) c) d) e) f) Q 5. [ marks 16] Differential equations ( Variable Separable /Reducible Variable Separable) Differential equations (Homogeneous/Exact /Linear/ Bernoulli’s D. E. ) Numerical Methods ( Gauss elimination/Gauss-seidel/Jacobi Method) Attempt any Three of the following [ marks 12 ] a) Application of D. E. b) Application of D. E. c) Numerical Methods (Bisection/ Regula - falsi / Newton- Raphson method ) d) Numerical Methods (Bisection/ Regula - falsi / Newton- Raphson method ) 16
![Q 6. Attempt any Four of the following [ marks 12] a) Numerical Methods Q 6. Attempt any Four of the following [ marks 12] a) Numerical Methods](http://slidetodoc.com/presentation_image_h2/67569e9c1dd829ca660e8a31751cb165/image-17.jpg)
Q 6. Attempt any Four of the following [ marks 12] a) Numerical Methods (Bisection/ Regula - falsi / Newton- Raphson method ) b) Probability Distribution (Binomial / Poisson’s/ Normal Distribution ) c) Probability Distribution (Binomial / Poisson’s/ Normal Distribution ) d) Probability Distribution (Binomial / Poisson’s/ Normal Distribution ) 17

• Presented By : - Mr. Vikas N. Bachhav Lecturer in Mathematics K. K. Wagh Polytechnic, Nashik Thank you 18
- Slides: 18