A practical t n threshold proxy signature scheme

A practical (t, n) threshold proxy signature scheme based on the RSA cryptosystem Source: IEEE TRANSACTIONS KNOWLEDGE AND DATA ENGINEERING, VOL 15, NO 5, SEPTEMBER/OCTOBER, 2003 Author: Min-Shiang Hwang, Eric Jui-Lin, Iuon-Chang Lin Speaker : 林育正 Team member: 童毅峰 林峻鋒 Date: Dec. 8, 2003

Outline n n n Introduction Proposed Scheme Discussion n n Property Analysis Comparisons Application Conclusion

Introduction 1 n Proxy signature: n The proxy signature allows proxy signers to sign messages on behalf of the original signer without exposing the original signer’s private key

Introduction 2 n (1, n) threshold proxy signature: n n A legal proxy signature can be generated by a designated proxy signer by using a proxy signing key. (t, n) threshold proxy signature: n (t, n) threshold proxy signature schemes allow any t or more proxy signers from a designated group of n members to cooperatively sign messages while (t-1) or less members cannot generate the legal proxy signature.

Introduction 3 n Proxy requirements n Secrecy: n n Proxy protected: n n The original signer’s private key must be kept secret. Only a delegated proxy signer can generate his partial proxy signature. Unforgeability: n (t-1) or less proxy signers have no capability of forging a valid proxy signature.

Introduction 4 n Proxy requirement (cont. ) n Non-repudiation: n n Time constraint: n n The original signer cannot deny having delegated the power of signing messages to the proxy signers. The proxy signers cannot deny that they having signed the message. The proxy signing keys can be used only during a stipulated period. Known signers: n For internal auditing purposes, the system is able to identify the actual signers in the proxy group.

Introduction 5 n n This paper propose a new (t, n) threshold proxy signature scheme based on the RSA cryptosystem. This new scheme only requires the Lagrange formula to share the proxy signing key.

Proposed Scheme n Three phases n n n The proxy sharing phase The proxy signature issuing phase The verification phase

Threshold proxy signature based on the RSA cryptosystem n n n P 0 ︰ Original signer P 1, P 2, . . . , Pn ︰Proxy signers Ni = pi × qi where pi and qi are two secret large primes. di is a private key for Pi and its corresponding public key be ei, such that di * ei = 1 mod Φ(Ni) = (pi - 1)(qi - 1)

Threshold proxy signature based on the RSA cryptosystem n n n The parameters ei and Ni can be published. The parameter di and Φ(Ni) are kept secret by the holder. [M]d mod Ni : M encrypted with Pi’s private key di [M]e mod Ni : M encrypted with Pi’s public key ei using the ordinary RSA cryptosystem. mw : contains period of proxy key, the identities of the proxy signers and the original signer, etc i i

Threshold proxy signature based on the RSA cryptosystem n n D : group proxy signature key generated by P 0 E : verification key of D

The Proxy Sharing Phase n Step 1. Proxy generation n D = d 0 mw mod Φ(N 0) E = e 0 mw mod Φ(N 0) P 0 publishes {mw, E, [mw || E] d 0 mod N 0}

The Proxy Sharing Phase n Step 2 (proxy sharing) n n Ki = f(x) = D + a 1 X + a 2 X 2 + … +at-1 Xt-1 mod Φ(N 0) where a 1, a 2, … at-1 are random numbers. The original signer P 0 computes Pi’s partial proxy signing key, ki = f(i) and sends [[Ki]d mod N 0 || ki ]e mod Ni to the proxy signer Pi, where i is user’s identity and for all Li Z i o

The Proxy Sharing Phase n Step 3. (proxy share generation) n n After receiving [[Ki]d mod N 0 || ki ]e mod Ni each proxy signer can decrypt the ciphertext to obtain {[ki]d 0 mod n 0, ki} Then each proxy signer Pi can confirm the validity of ki and keep it secret. o i

The Proxy Signature Issuing Phase n Step 1. n n n Each member of T signs the message M with his partial proxy signing key ki, where i T. The partial proxy signature si for each actual proxy signer pi. si = M (Li × Ki) mod N 0 Li = Π –j / i-j i, jεT, j ≠ i Each actual proxy signer sends {[si]d mod Ni, si} to the combiner. i

The Proxy Signature Issuing Phase n Step 2. n The combiner verifies the si using the public key of the proxy signer Pi, and collects [si]d mod Ni. S: the proxy signature on message M S=Π s mod N 0 iεT i i n n = iεT Π(M Li × Ki) mod N 0 = MΣi εT (Li × f(i) ) mod N 0 = M f(0) mod N 0 = MD mod N 0

The Verification Phase n n Ni, ei, mw, and E are publicly known Step 1. n n n Any receiver computes mw and E with the original signer’s public key. The receiver checks the validity of the stipulated period. If the period has expired, the proxy verification key is invalid.

The Verification Phase n Step 2. n SE mod N 0 = (MD)E mod N 0 mw (d × e ) 0 0 =M mod N 0 =M

The Verification Phase n Step 3. n For internal auditing purposes, the original signer can differentiate the actual signers from the signatures [si]d mod Ni on message si, where i t. i

Discussion – Property analysis n n n Secrecy Proxy protected Unforgability Non-repudiation Time constraint Known signer

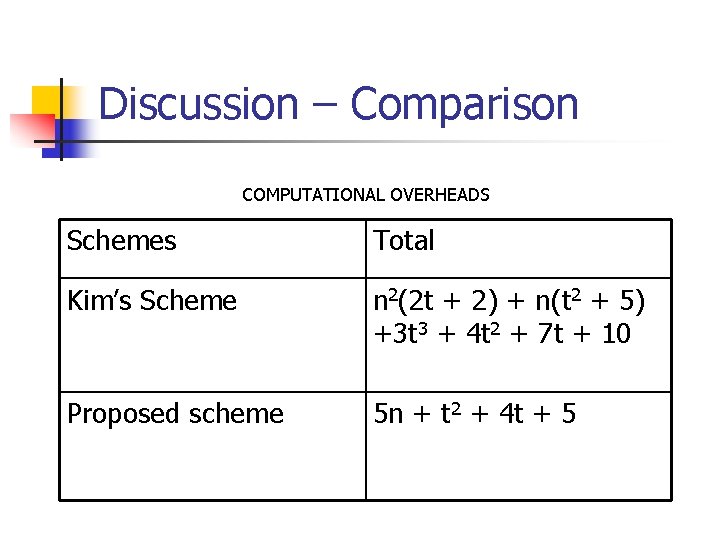
Discussion – Comparison COMPUTATIONAL OVERHEADS Schemes Total Kim’s Scheme n 2(2 t + 2) + n(t 2 + 5) +3 t 3 + 4 t 2 + 7 t + 10 Proposed scheme 5 n + t 2 + 4 t + 5

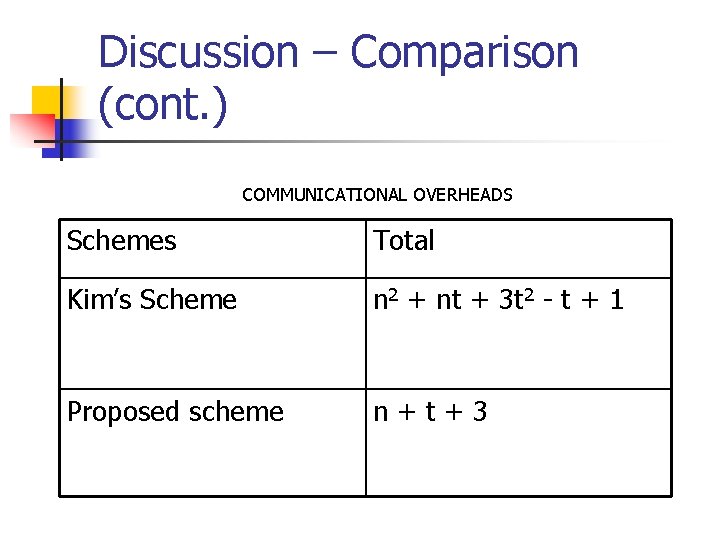
Discussion – Comparison (cont. ) COMMUNICATIONAL OVERHEADS Schemes Total Kim’s Scheme n 2 + nt + 3 t 2 - t + 1 Proposed scheme n+t+3

Application n n Mobile Agent Electronic Contract

Conclusion n n Flexibly choose threshold Repeatedly use of the participant’s RSA key pairs which can also be used in other work Put time constraints on the threshold delegation Identify the actual signers