A Practical Algorithm to Find the Best Episode

A Practical Algorithm to Find the Best Episode Patterns Masahiro Hirao, Shunsuke Inenaga, Ayumi Shinohara, Masayuki Takeda, and Setsuo Arikawa

Backgrounds and Motivation n To distinguish given two sets of strings To grade up BONSAI system - so that it works faster and can also deal with episode patterns - n

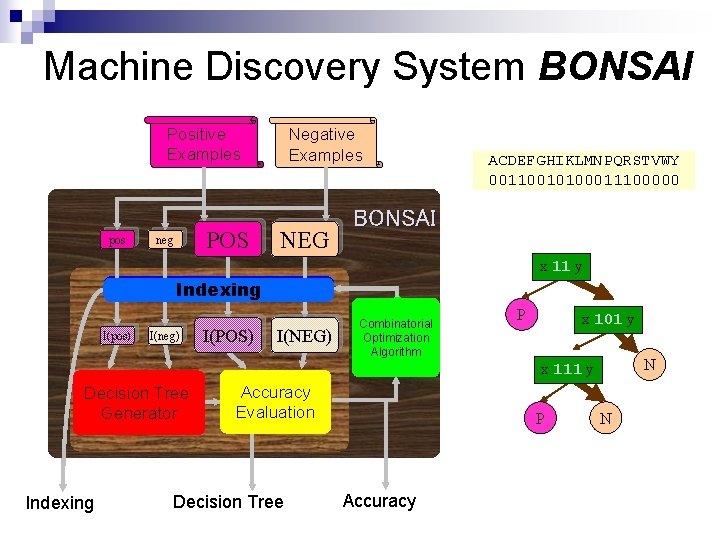
Machine Discovery System BONSAI Positive Examples pos POS neg Negative Examples NEG ACDEFGHIKLMNPQRSTVWY 00110010100011100000 BONSAI x 11 y Indexing I(pos) I(neg) I(POS) I(NEG) Combinatorial Optimization Algorithm P x 101 y N x 111 y Decision Tree Generator Indexing Accuracy Evaluation Decision Tree P Accuracy N

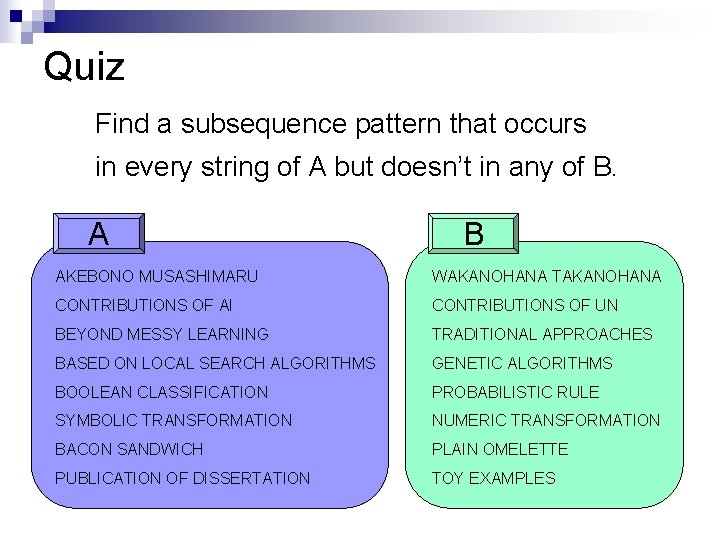
Quiz Find a subsequence pattern that occurs in every string of A but doesn’t in any of B. A B AKEBONO MUSASHIMARU WAKANOHANA TAKANOHANA CONTRIBUTIONS OF AI CONTRIBUTIONS OF UN BEYOND MESSY LEARNING TRADITIONAL APPROACHES BASED ON LOCAL SEARCH ALGORITHMS GENETIC ALGORITHMS BOOLEAN CLASSIFICATION PROBABILISTIC RULE SYMBOLIC TRANSFORMATION NUMERIC TRANSFORMATION BACON SANDWICH PLAIN OMELETTE PUBLICATION OF DISSERTATION TOY EXAMPLES

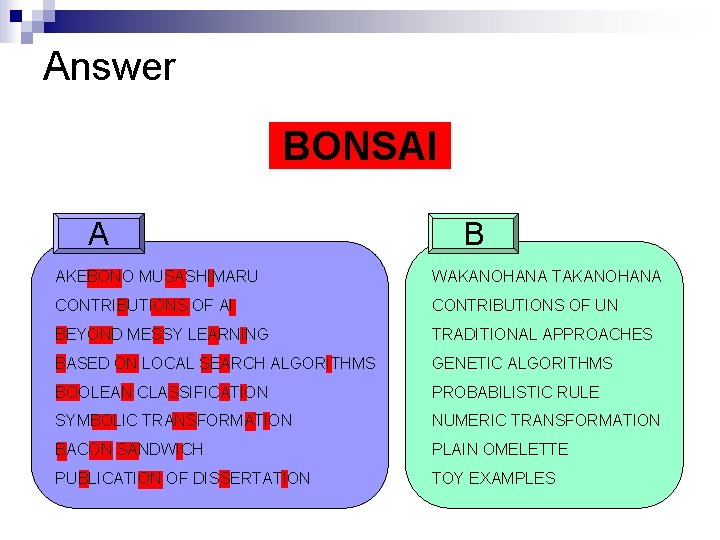
Answer BONSAI A B AKEBONO MUSASHIMARU WAKANOHANA TAKANOHANA CONTRIBUTIONS OF AI CONTRIBUTIONS OF UN BEYOND MESSY LEARNING TRADITIONAL APPROACHES BASED ON LOCAL SEARCH ALGORITHMS GENETIC ALGORITHMS BOOLEAN CLASSIFICATION PROBABILISTIC RULE SYMBOLIC TRANSFORMATION NUMERIC TRANSFORMATION BACON SANDWICH PLAIN OMELETTE PUBLICATION OF DISSERTATION TOY EXAMPLES

Generalization of the Patterns An episode pattern is a pair <p, k> where p is a string and k is an integer. A substring pattern is a pair <p, |p|>. A subsequence pattern is a pair <p, >.

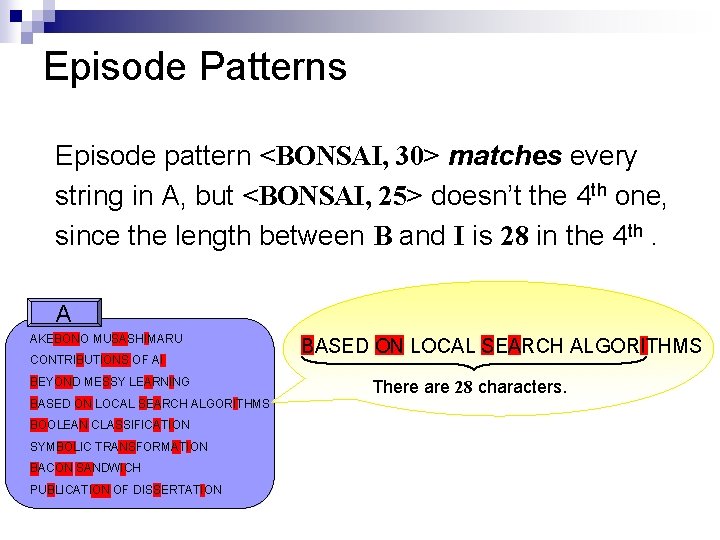
Episode Patterns Episode pattern <BONSAI, 30> matches every string in A, but <BONSAI, 25> doesn’t the 4 th one, since the length between B and I is 28 in the 4 th. A AKEBONO MUSASHIMARU CONTRIBUTIONS OF AI BEYOND MESSY LEARNING BASED ON LOCAL SEARCH ALGORITHMS BOOLEAN CLASSIFICATION SYMBOLIC TRANSFORMATION BACON SANDWICH PUBLICATION OF DISSERTATION BASED ON LOCAL SEARCH ALGORITHMS There are 28 characters.

Problem to Find a Consistent Pattern Find a pattern which is common to the positive examples but never occurs in the negative examples. Finding a consistent ・substring is solvable in linear time. ・subsequence is NP-hard. ・episode pattern is NP-hard.

Finding the Best Episode Patterns Input: Sets S, T S * of strings n Output: An episode pattern <p, k> that maximizes function f(x<p, k>, y<p, k>). n x<p, k> : The num. of strings in S which <p, k> matches. y<p, k> : The num. of strings in T which <p, k> matches. It depends on an application what function we use as f, where function f must be conic.

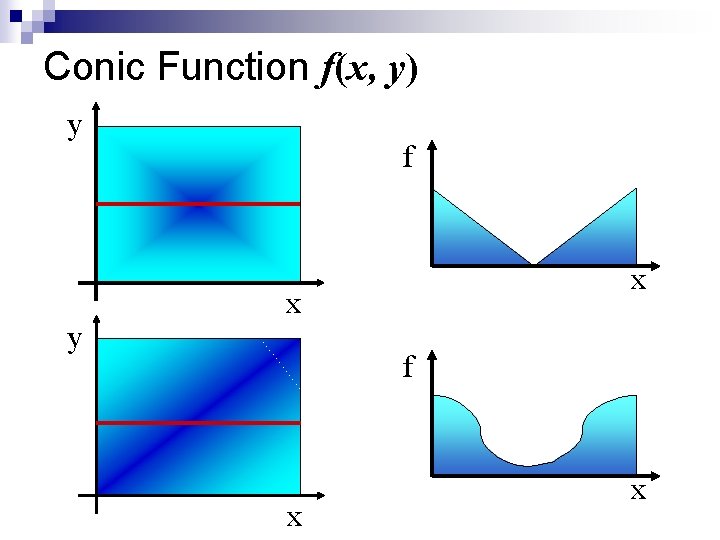
Conic Function f(x, y) y y f x x

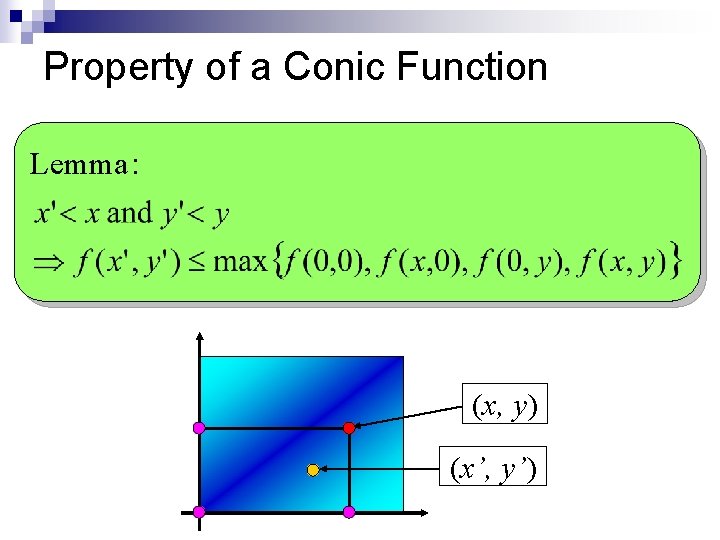
Property of a Conic Function Lemma： (x, y) (x’, y’)

Pruning Lemma x : the number of strings in S which <p, k> matches y : the number of strings in T which <p, k> matches p is a subsequence of q and k Matched strings in T y y’ <p, k> <q, l> f(x’, y’) x’ x Matched Strings in S f(0, 0) f(x, 0) max f(0, y) f(x, y) l

Pseudo-code of the Algorithm 1 string Find. Best. Episode(String. Set S, T, int d) 2 string prefix, p; 3 episode. Pattern max. Seq; /* pair of string and int */ 4 double upper. Bound = ; max. Val = ; val; 5 int k’; 6 Compact. Repr x, y; /* CRS */ 7 Priority. Queue queue; /* Best First Search */ 8 queue. push(“”, ); 9 while not queue. empty() do 10 (prefix, upper. Bound) = queue. pop(); 11 if upper. Bound < max. Val then break; 12 foreach c S do 13 p = prefix + c; /* string concatenation */ 14 x = S. crs(p); 15 y = T. crs(p); 16 k’ = argmaxk{f(x<p, k>, y<p, k>)}; val = f(x<p, k’>, y<p, k’>); 17 if val > max. Val then 18 max. Val = val; max. Episode = <p, k’>; 19 upper. Bound = max{ f(x<p, >, y<p, >), f(x<p, >, 0), f(0, y<p, 20 if upper. Bound > max. Val and |p| < d then 21 queue. push(p, upper. Bound); 22 return max. Episode; >), f(0, 0)};

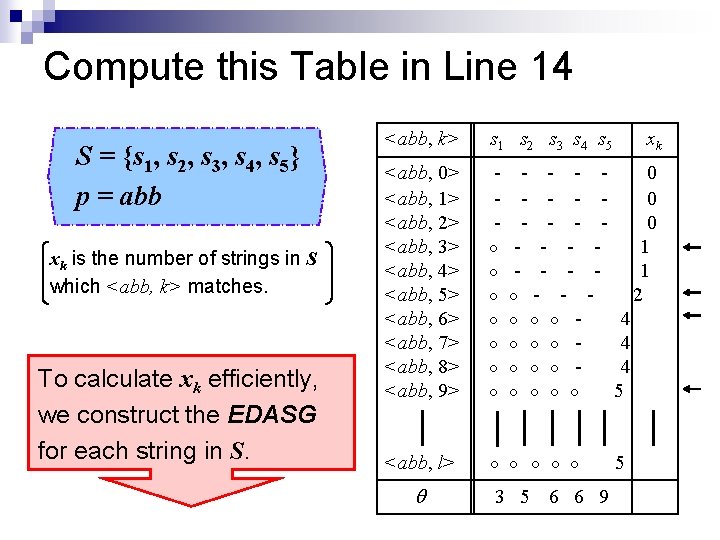
Compute this Table in Line 14 S = {s 1, s 2, s 3, s 4, s 5} p = abb xk is the number of strings in S which <abb, k> matches. To calculate xk efficiently, we construct the EDASG for each string in S. <abb, k> s 1 s 2 s 3 s 4 s 5 <abb, 0> <abb, 1> <abb, 2> <abb, 3> <abb, 4> <abb, 5> <abb, 6> <abb, 7> <abb, 8> <abb, 9> - - - - 0 ○ - - - 1 ○ ○ - - 2 ○ ○ ○ ○ 4 ○ ○ ○ 5 <abb, l> ○ ○ ○ q 3 5 6 6 9 xk 5

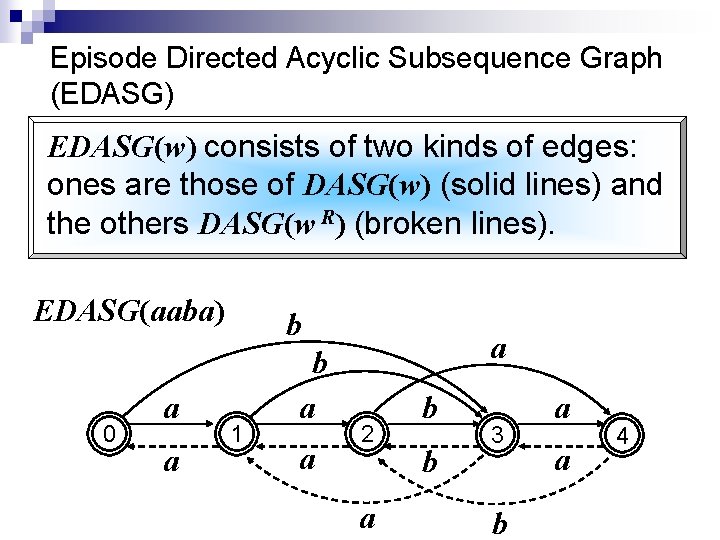
Episode Directed Acyclic Subsequence Graph (EDASG) EDASG(w) consists of two kinds of edges: ones are those of DASG(w) (solid lines) and the others DASG(w R) (broken lines). EDASG(aaba) 0 a a b 1 b a a a 2 a b b 3 b a a 4

Compact Representation of {xk}k=0 We consider the numerical sequence {xk}k=0. In the table above we only need to focus on the elements of xk where the value changes, which have been indicated by “←”. Then we can represent {xk}k=0 as a list of pairs (k, xk) such that xk-1 = xk , like below. {xk}k=0 = 0, 0, 0, 1, 1, 2, 4, 4, 4, 5, 5, … = (3, 1), (5, 2), (6, 4), (9, 5) = x

Time Complexity of Computing CRS Computing xk for a single k (0 k ∞) takes O(||S||m) time, where m = |p|. An important fact is the time complexity to compute the CRS for p S * is also O(|S|ml+|S|) = O(||S||m). l is the length of the longest string in S. ||S|| denotes the total length of the strings in S.

What to Do in Line 16 n k’ is computed by the comparison of x and y. x = {(3, 1), (5, 2), (6, 4), (9, 5)} y = {(3, 2), (5, 3), (6, 6), (8, 8)} We compute f(x, y) only for a pair circled by. k x k y 0 1 2 3 4 5 6 7 8 9 0 0 0 1 1 2 4 4 4 5 0 1 2 3 4 5 6 7 8 9 0 0 0 2 2 3 6 6 8 8

Related Work “More Speed and More Pattern Variations for Knowledge Discovery System BONSAI” Hideo Bannai, Keisuke Iida, Ayumi Shinohara, Masayuki Takeda, and Satoru Miyano Int. Conf. on Genome Informatics 2001 (to appear)