A Polynomial Time Matching Algorithm of Ordered Tree
![Therefore, (v’, 0, 0) CS(u) if and only if t[v’] matches T[u]. (v’, 0,](https://slidetodoc.com/presentation_image/70a9307f1fdebe083b1053f4a93d2013/image-17.jpg "Therefore, (v’, 0, 0) CS(u) if and only if t[v’] matches T[u]. (v’, 0,")
- Slides: 38
A Polynomial Time Matching Algorithm of Ordered Tree Patterns having Height-Constrained Variables Kazuhide Aikou 1, Yusuke Suzuki 1, 2, Takayoshi Shoudai 1, Tomoyuki Uchida 2, Tetsuhiro Miyahara 2 1. Department of Informatics, Kyushu University, Japan 2. Faculty of Information Sciences, Hiroshima City University, Japan
Contents 1. Backgrounds and Motivations 2. Preliminaries - Ordered Term Trees - Height-Constrained Variables 3. A Matching Algorithm of Ordered Term Trees having Height-Constrained Variables 4. Conclusions and Future Works
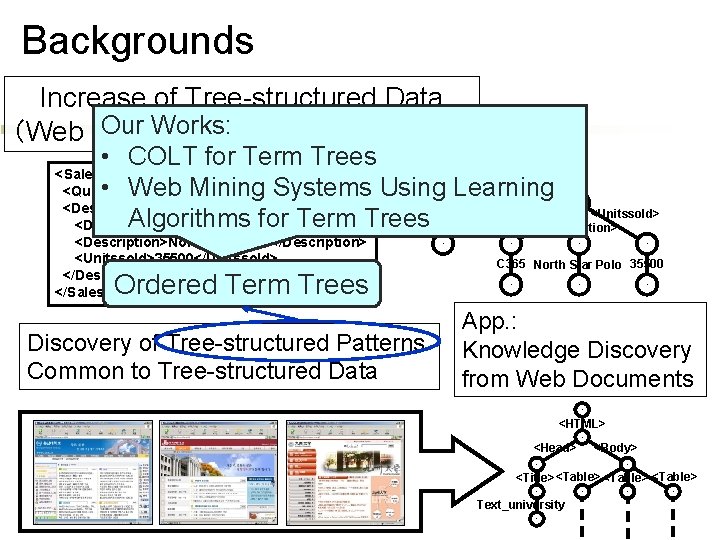
Backgrounds Increase of Tree-structured Data Our Works: HTML/XML, etc. ） （Web Documents, <Salesperiod> • COLT for Term Trees <Design> • Web Mining Systems Using<Quarter> Learning <Designnumber> <Unitssold> Algorithms for Term Trees Winter 1998 <Description> <Salesperiod> <Quarter>Winter 1998</Quarter> <Designnumber>C 365</Designnumber> <Description>North Star Polo</Description> <Unitssold>35500</Unitssold> </Design> </Salesperiod> Ordered Term Trees Discovery of Tree-structured Patterns Common to Tree-structured Data C 365 North Star Polo 35500 App. : Knowledge Discovery from Web Documents <HTML> <Head> <Body> <Title><Table> Text_university
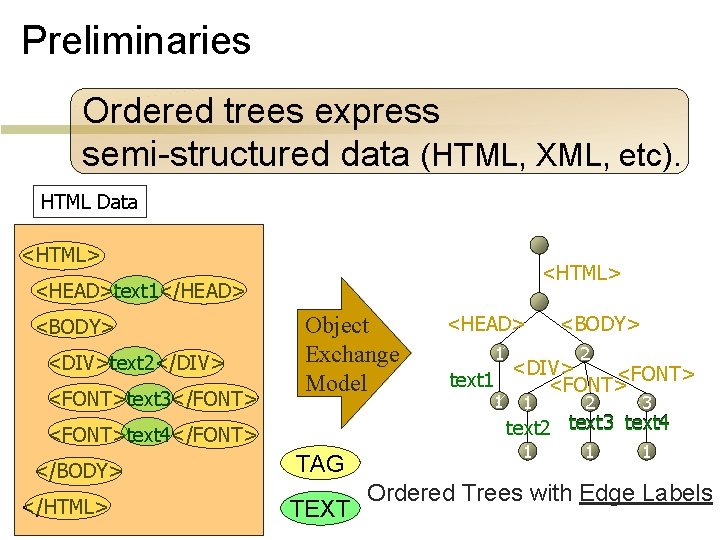
Preliminaries Ordered trees express semi-structured data (HTML, XML, etc). HTML Data <HTML> <HEAD>text 1</HEAD> <BODY> <DIV>text 2</DIV> <FONT>text 3</FONT> Object Exchange Model <FONT>text 4</FONT> </BODY> TAG </HTML> TEXT <HEAD> 1 text 1 1 <BODY> 2 <DIV> <FONT> 1 2 3 1 1 1 text 2 text 3 text 4 Ordered Trees with Edge Labels
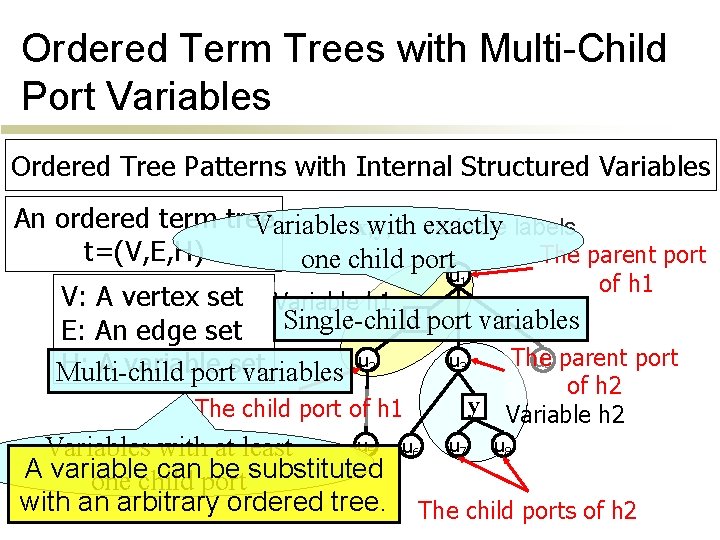
Ordered Term Trees with Multi-Child Port Variables Ordered Tree Patterns with Internal Structured Variables An ordered term tree Variablesx, y, . . . : with variable exactly labels t=(V, E, H) The parent port one child port u 1 of h 1 V: A vertex set Variable h 1 E: An edge set Single-childx port variables The u 2 u 3 u 4 parent port H: A variable set Multi-child port variables of h 2 y The child port of h 1 u 5 Variables with at least A variable canport be substituted one child with an arbitrary ordered tree. u 6 u 7 Variable h 2 u 8 The child ports of h 2
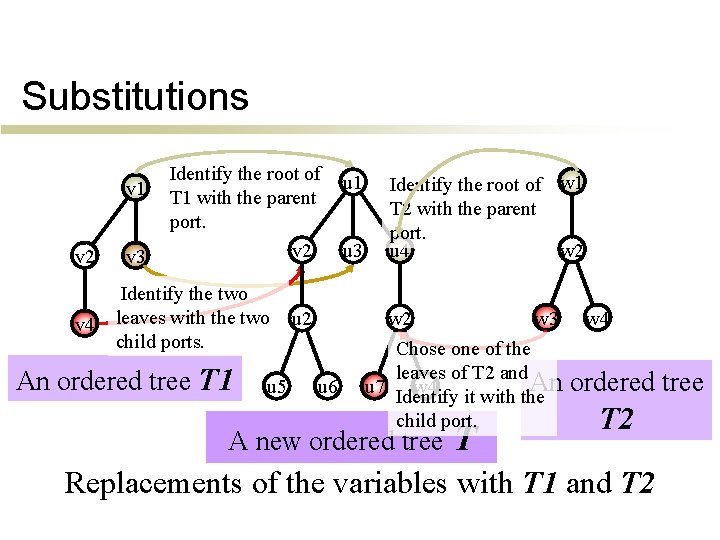
Substitutions v 1 v 2 v 4 v 3 Identify the root of u 1 T 1 with the parent x port. v 2 u 3 Identify the two leaves with the twou 5 u 2 u 6 child ports. An ordered tree T 1 u 5 u 6 Identify the root of w 1 T 2 with the parent port. w 2 vi u 4 y vi w 2 u 7 w 3 Chose one of the leaves of T 2 and An u 7 w 4 Identify it with the child port. An A new ordered termtree. Tt w 4 ordered tree T 2 Replacements of the variables with T 1 and T 2
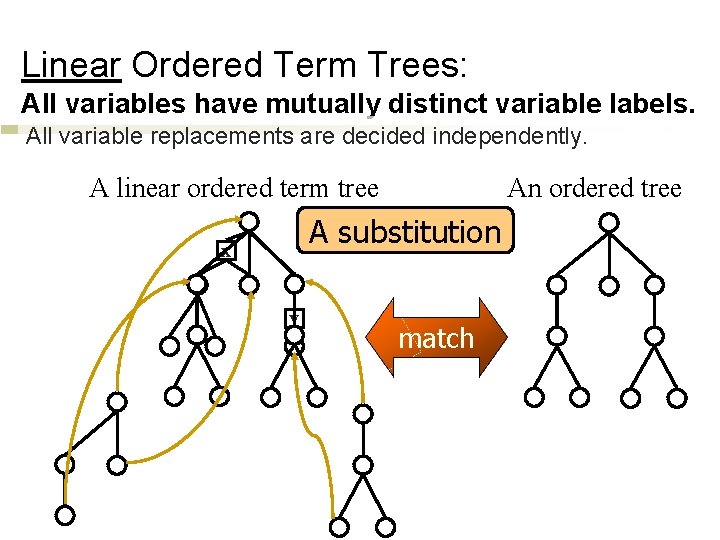
Linear Ordered Term Trees: All variables have mutually distinct variable labels. All variable replacements are decided independently. An ordered tree A linear ordered term tree A substitution x y match
Matching Problem for Linear Ordered Term Trees with Multi-Child Port Variables INPUT T: an ordered tree; t: a linear ordered term tree with multi-child port variables. PROBLEM Does t match T? This matching problem is computed in O(n. N) time, where n is the number of vertices in t and N is the number of vertices in T [Suzuki et al. , ILP 02].
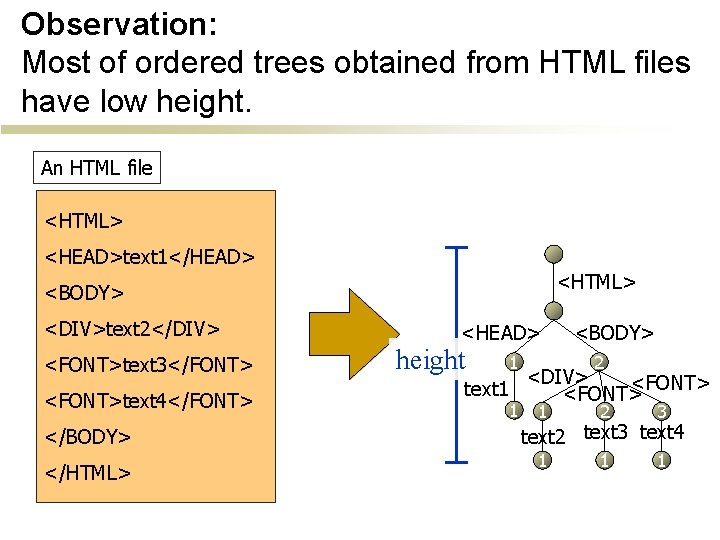
Observation: Most of ordered trees obtained from HTML files have low height. An HTML file <HTML> <HEAD>text 1</HEAD> <HTML> <BODY> <DIV>text 2</DIV> <FONT>text 3</FONT> <FONT>text 4</FONT> </BODY> </HTML> <HEAD> height text 1 1 1 <BODY> 2 <DIV> <FONT> 1 2 3 1 1 1 text 2 text 3 text 4
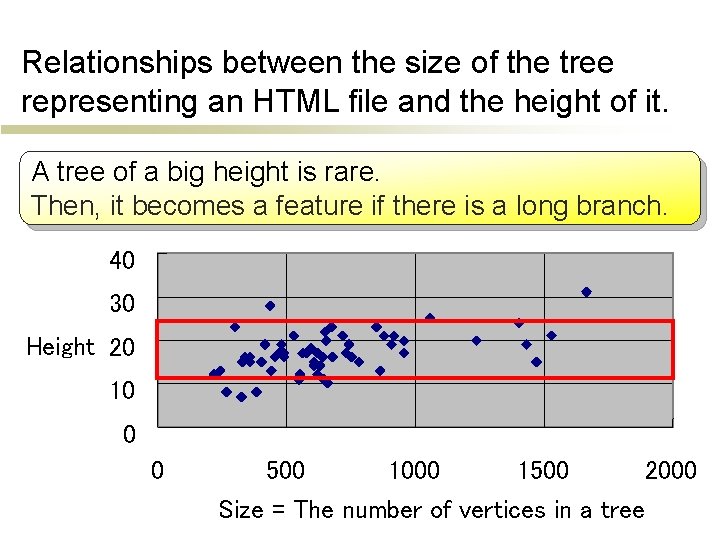
Relationships between the size of the tree representing an HTML file and the height of it. A tree of a big height is rare. Then, it becomes a feature if there is a long branch. 40 30 Height 20 10 0 0 500 1000 1500 2000 Size = The number of vertices in a tree
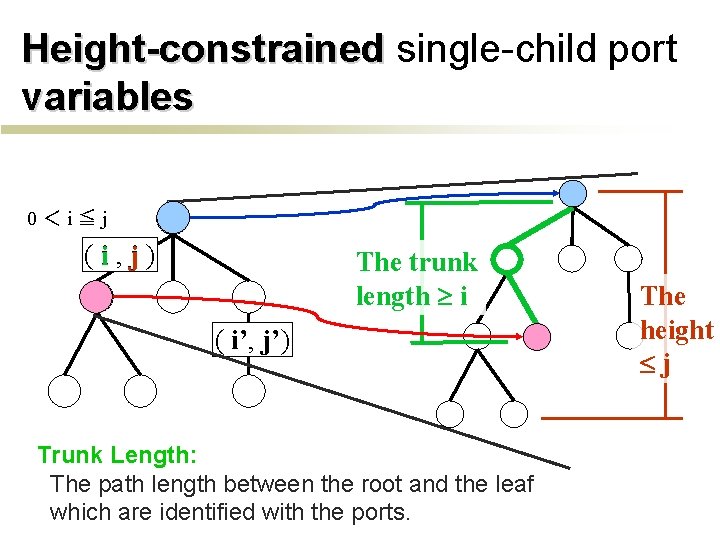
Height-constrained single-child port variables 0＜i≦j (i, j) The trunk length i ( i’, j’) Trunk Length: The path length between the root and the leaf which are identified with the ports. The height j
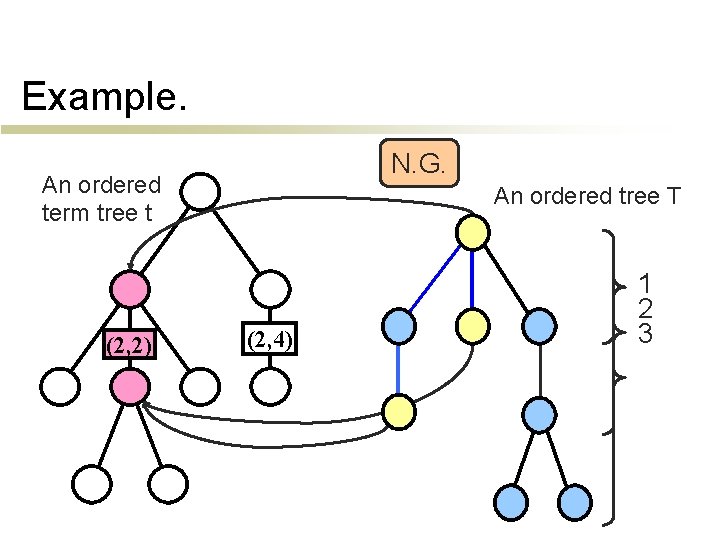
Example. N. G. O. K An ordered term tree t (2, 2) An ordered tree T (2, 4) 1 2 3
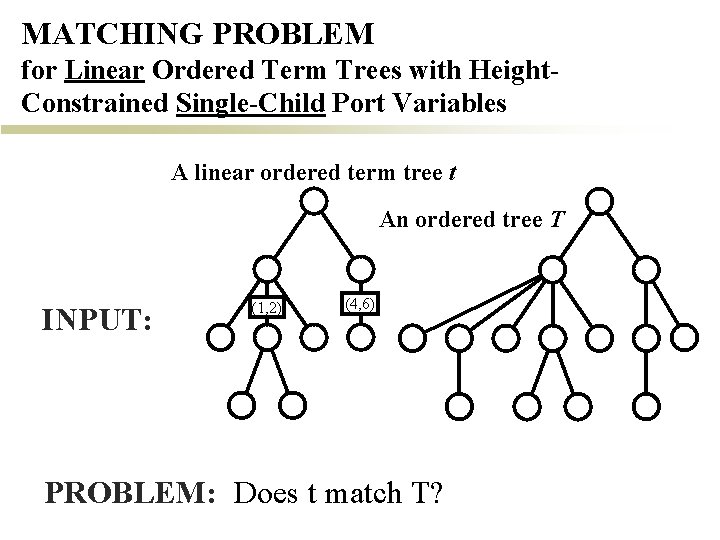
MATCHING PROBLEM for Linear Ordered Term Trees with Height. Constrained Single-Child Port Variables A linear ordered term tree t An ordered tree T INPUT: (1, 2) (4, 6) PROBLEM: Does t match T?
Main Theorem n MATCHING PROBLEM for Linear Ordered Term Trees with Height-Constrained Single-Child Port Variables is computed in O(N max{n. Dmax, S}) time, where n: the number of vertices of t, N: the number of vertices of T, S: the total amount of the lowest trunk lengths of all variables of t, Dmax: the maximum number of children of a vertex of T.
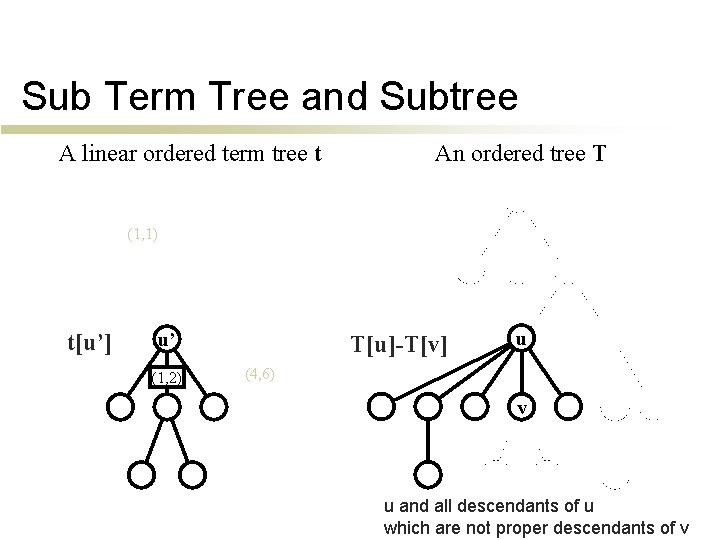
Sub Term Tree and Subtree A linear ordered term tree t An ordered tree T (1, 1) t[u’] u’ (1, 2) T[u]-T[v] u (4, 6) v u and all descendants of u which are not proper descendants of v
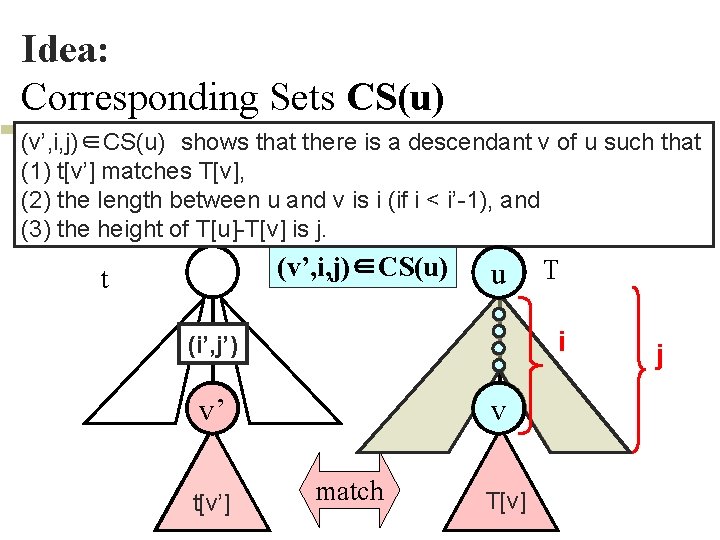
Idea: Corresponding Sets CS(u) (v’, i, j)∈CS(u) shows that there is a descendant v of u such that t=(Vt, ET[v], (1) t[v’] matches t, Ht): a term tree, T=(VT, ET): a tree. (2)CS(u) V the length between u and v is i (if i < i’-1), and t×N×N : a corresponding set of a vertex u VT. (3) the height of T[u]-T[v] is j. (v’, i, j)∈CS(u) t u i (i’, j’) v’ t[v’] T v match T[v] j
Therefore, (v’, 0, 0) CS(u) if and only if t[v’] matches T[u]. (v’, 0, 0)∈CS(u) t v’ (i’, j’) u T match (the root of t, 0, 0) CS(the root of T) if and only if t matches T.
Algorithm Matching(t, T) Matching 1 Initialization; while there is an unmarked vertex u of T do begin Mark u; 2 VID-Inheriting(u); 3 C-Set-Attaching(u) end
Algorithm Matching(t, T) Matching Initialization; while there is an unmarked vertex u of T do begin Mark u; VID-Inheriting(u); C-Set-Attaching(u) end
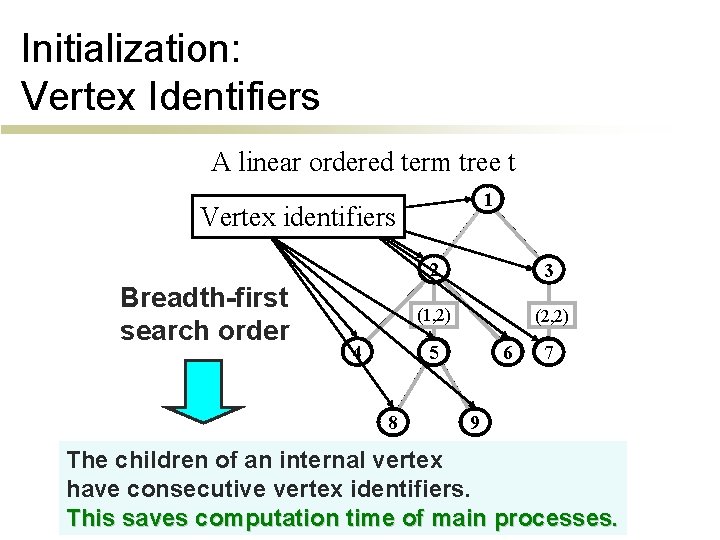
Initialization: Vertex Identifiers A linear ordered term tree t 1 Vertex identifiers Breadth-first search order 4 2 3 (1, 2) (2, 2) 5 8 6 7 9 The children of an internal vertex have consecutive vertex identifiers. This saves computation time of main processes.
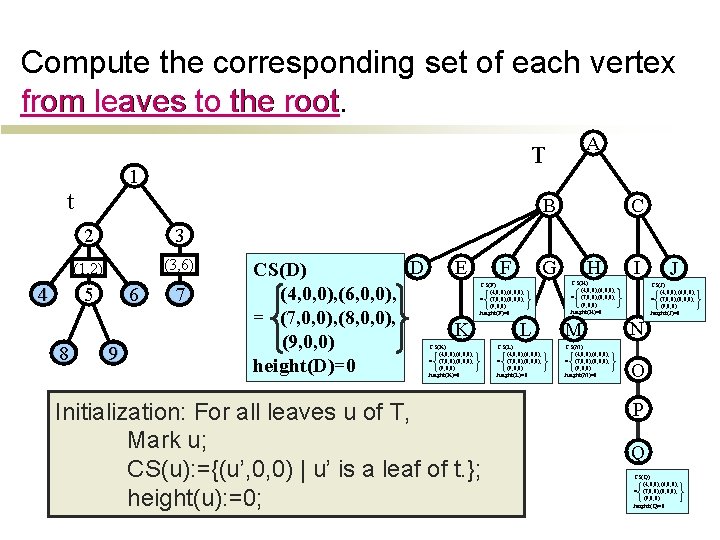
Compute the corresponding set of each vertex from leaves to the root. 1 t 4 B 2 3 (1, 2) (3, 6) 5 8 A T 6 9 7 D CS(D) (4, 0, 0), (6, 0, 0), = (7, 0, 0), (8, 0, 0), (9, 0, 0) height(D)=0 F E CS(K) (4, 0, 0), (6, 0, 0), = (7, 0, 0), (8, 0, 0), (9, 0, 0) height(K)=0 Initialization: For all leaves u of T, Mark u; CS(u): ={(u’, 0, 0) | u’ is a leaf of t. }; height(u): =0; H G CS(F) (4, 0, 0), (6, 0, 0), = (7, 0, 0), (8, 0, 0), (9, 0, 0) height(F)=0 K C L CS(L) (4, 0, 0), (6, 0, 0), = (7, 0, 0), (8, 0, 0), (9, 0, 0) height(L)=0 I CS(H) (4, 0, 0), (6, 0, 0), = (7, 0, 0), (8, 0, 0), (9, 0, 0) height(H)=0 J CS(J) (4, 0, 0), (6, 0, 0), = (7, 0, 0), (8, 0, 0), (9, 0, 0) height(J)=0 M N CS(M) (4, 0, 0), (6, 0, 0), = (7, 0, 0), (8, 0, 0), (9, 0, 0) height(M)=0 O P Q CS(Q) (4, 0, 0), (6, 0, 0), = (7, 0, 0), (8, 0, 0), (9, 0, 0) height(Q)=0
Algorithm Matching(t, T) Matching Initialization; while there is an unmarked vertex u of T do begin Mark u; VID-Inheriting(u); C-Set-Attaching(u) end
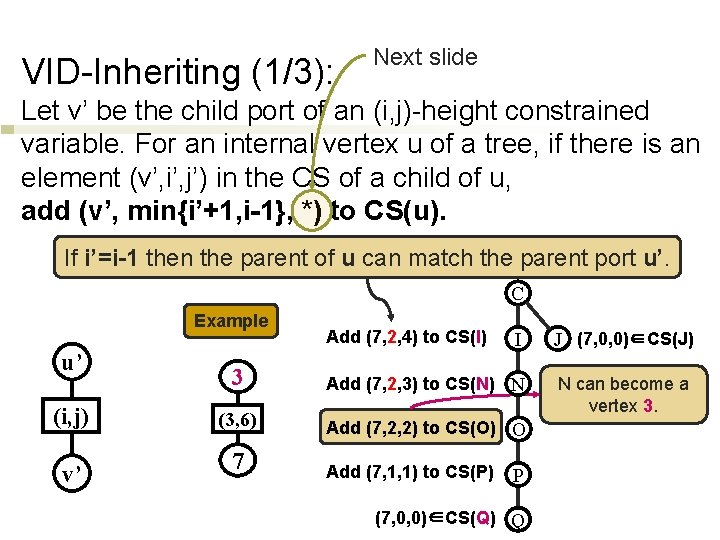
VID-Inheriting (1/3): Next slide Let v’ be the child port of an (i, j)-height constrained variable. For an internal vertex u of a tree, if there is an element (v’, i’, j’) in the CS of a child of u, add (v’, min{i’+1, i-1}, *) to CS(u). If i’=i-1 then the parent of u can match the parent port u’. C Example u’ (i, j) v’ 3 (3, 6) 7 Add (7, 2, 4) to CS(I) I J (7, 0, 0)∈CS(J) Add (7, 2, 3) to CS(N) N N can become a vertex 3. Add (7, 2, 2) to CS(O) O Add (7, 1, 1) to CS(P) P (7, 0, 0)∈CS(Q) Q
VID-Inheriting (2/3): Case: At least two children have (v’, i’, *) for a vertex v’ and an integer i’. T 3 (4, 6) 7 (7, 1, 1)∈CS(b) height(b)=4 4 a b (7, 2, 4)∈CS(a) (7, 2, 4) , (7, 2, 5)∈CS(a) c (7, 1, 3)∈CS(c) height(c)=3 3 Choose the smallest height
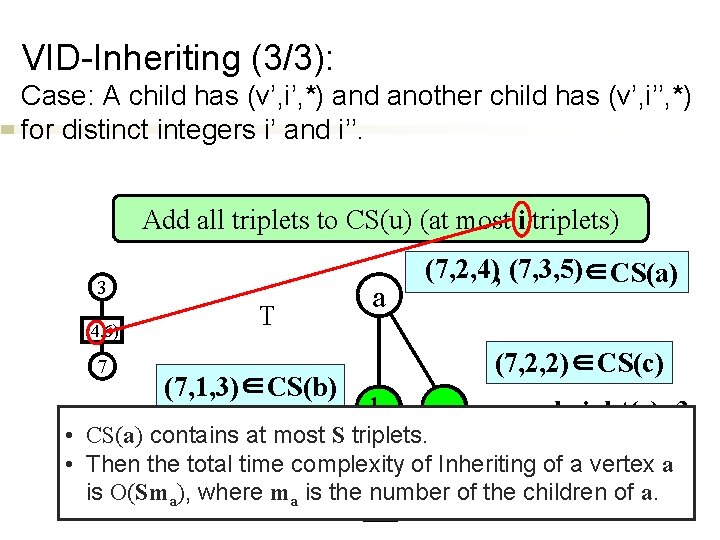
VID-Inheriting (3/3): Case: A child has (v’, i’, *) and another child has (v’, i’’, *) for distinct integers i’ and i’’. Add all triplets to CS(u) (at most i triplets) 3 (4, 6) 7 T a (7, 2, 4), (7, 3, 5) ∈CS(a) (7, 1, 3)∈CS(b) c b height(b)=4 • CS(a) contains at most S triplets. (7, 2, 2)∈CS(c) height(c)=3 3 • Then the total time complexity of Inheriting of a vertex a 4 is O(Sma), where ma is the number of the children of a.
Algorithm Matching(t, T) Matching Initialization; while there is an unmarked vertex u of T do begin Mark u; VID-Inheriting(u); C-Set-Attaching(u) end
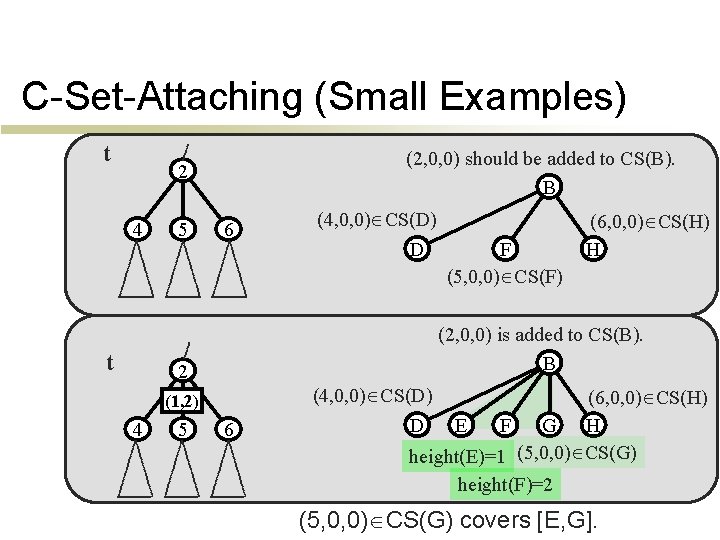
C-Set-Attaching (Small Examples) t (2, 0, 0) should be added to CS(B). B 2 4 t 5 6 (4, 0, 0) CS(D) D (2, 0, 0) is added to CS(B). B 2 (4, 0, 0) CS(D) (1, 2) 4 5 F (5, 0, 0) CS(F) (6, 0, 0) CS(H) H 6 (6, 0, 0) CS(H) D E F G H height(E)=1 (5, 0, 0) CS(G) height(F)=2 (5, 0, 0) CS(G) covers [E, G].
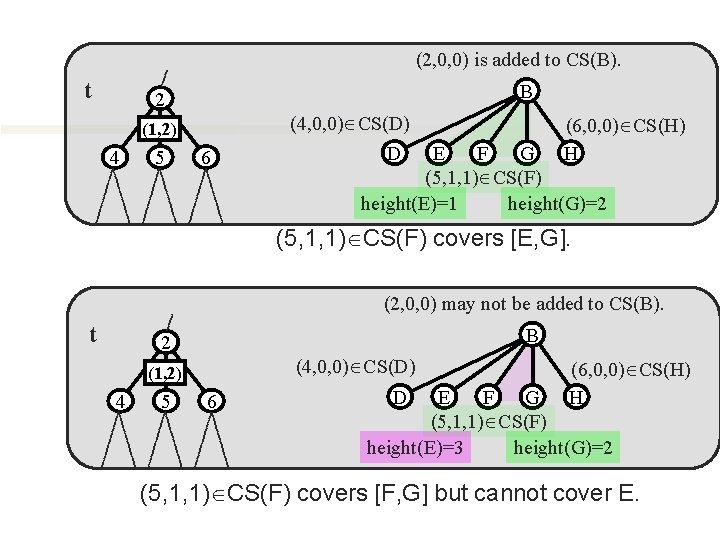
(2, 0, 0) is added to CS(B). t B 2 (4, 0, 0) CS(D) (1, 2) 4 5 6 (6, 0, 0) CS(H) H D E F G (5, 1, 1) CS(F) height(E)=1 height(G)=2 (5, 1, 1) CS(F) covers [E, G]. (2, 0, 0) may not be added to CS(B). t B 2 (4, 0, 0) CS(D) (1, 2) 4 5 6 D (6, 0, 0) CS(H) H E F G (5, 1, 1) CS(F) height(E)=3 height(G)=2 (5, 1, 1) CS(F) covers [F, G] but cannot cover E.
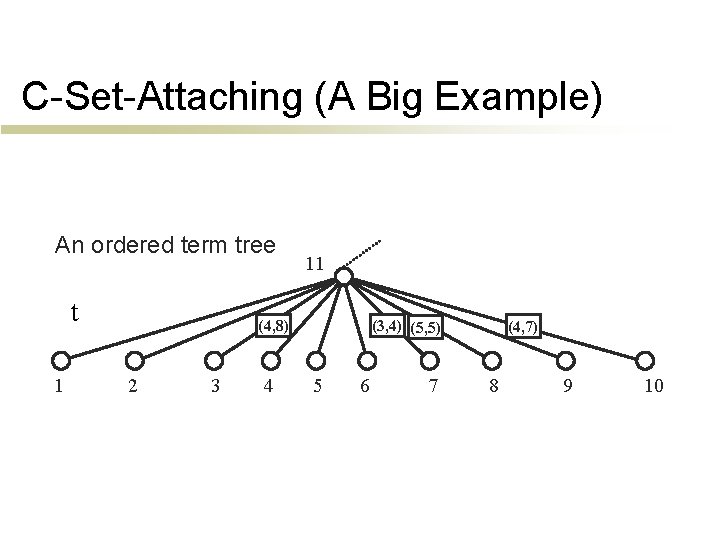
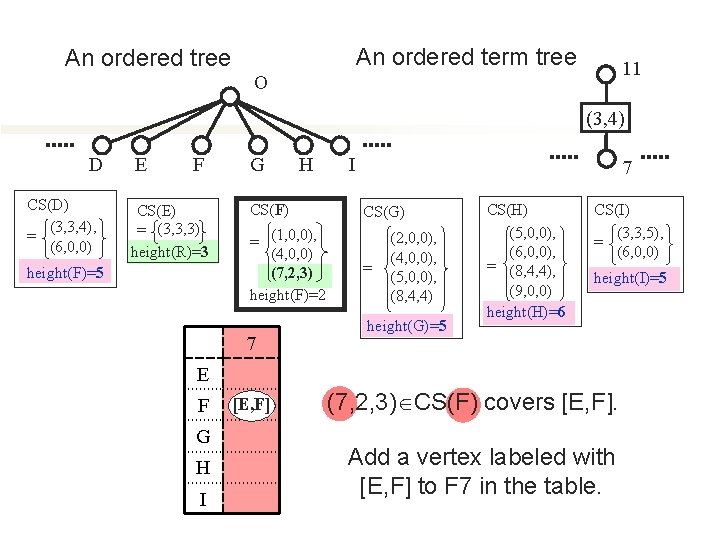
C-Set-Attaching (A Big Example) An ordered term tree t 1 11 (4, 8) 2 3 4 (3, 4) (5, 5) 5 6 7 (4, 7) 8 9 10
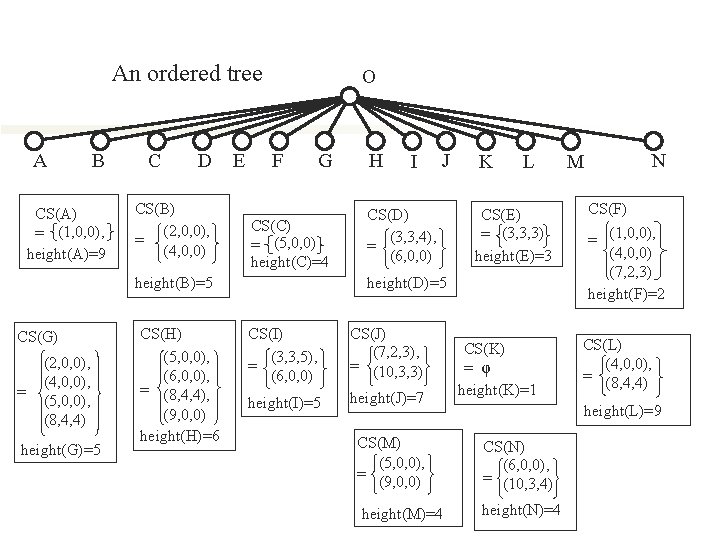
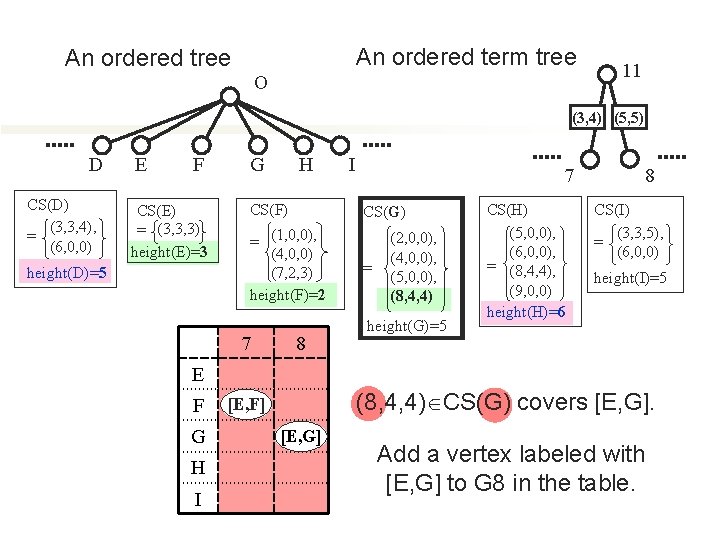
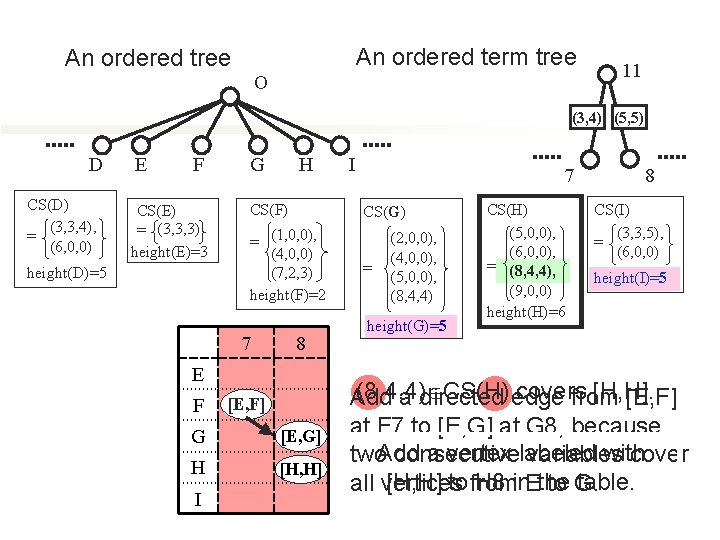
An ordered tree A B CS(A) = (1, 0, 0), height(A)=9 C D CS(B) (2, 0, 0), = (4, 0, 0) E O F G CS(C) = (5, 0, 0) height(C)=4 = (2, 0, 0), (4, 0, 0), (5, 0, 0), (8, 4, 4) height(G)=5 CS(H) (5, 0, 0), (6, 0, 0), = (8, 4, 4), (9, 0, 0) height(H)=6 I J CS(D) (3, 3, 4), = (6, 0, 0) K L CS(E) = (3, 3, 3) height(E)=3 height(D)=5 height(B)=5 CS(G) H CS(I) (3, 3, 5), = (6, 0, 0) CS(J) (7, 2, 3), = (10, 3, 3) height(I)=5 height(J)=7 CS(K) = φ height(K)=1 N M CS(F) = (1, 0, 0), (4, 0, 0) (7, 2, 3) height(F)=2 CS(L) (4, 0, 0), = (8, 4, 4) height(L)=9 CS(M) (5, 0, 0), = (9, 0, 0) CS(N) (6, 0, 0), = (10, 3, 4) height(M)=4 height(N)=4
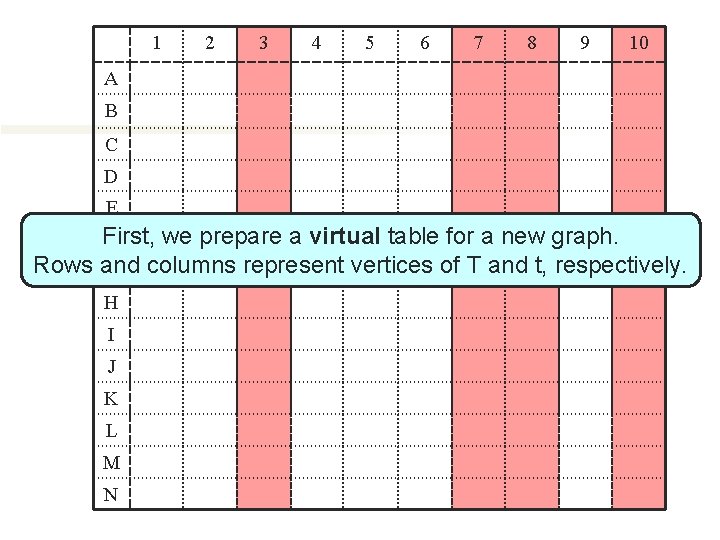
1 2 3 4 5 6 7 8 9 10 A B C D E First, we prepare a virtual table for a new graph. F Rows and G columns represent vertices of T and t, respectively. H I J K L M N
An ordered term tree An ordered tree 11 O (3, 4) D CS(D) (3, 3, 4), = (6, 0, 0) E F CS(E) = (3, 3, 3) height(R)=3 height(F)=5 G H CS(F) = (1, 0, 0), (4, 0, 0) (7, 2, 3) height(F)=2 7 I 7 CS(G) = (2, 0, 0), (4, 0, 0), (5, 0, 0), (8, 4, 4) height(G)=5 CS(H) (5, 0, 0), (6, 0, 0), = (8, 4, 4), (9, 0, 0) height(H)=6 CS(I) (3, 3, 5), = (6, 0, 0) height(I)=5 E F G H I [E, F] (7, 2, 3) CS(F) covers [E, F]. Add a vertex labeled with [E, F] to F 7 in the table.
An ordered term tree An ordered tree O 11 (3, 4) (5, 5) D CS(D) (3, 3, 4), = (6, 0, 0) E F CS(E) = (3, 3, 3) height(E)=3 height(D)=5 G H CS(F) 7 CS(G) = (1, 0, 0), (4, 0, 0) (7, 2, 3) height(F)=2 7 I 8 = (2, 0, 0), (4, 0, 0), (5, 0, 0), (8, 4, 4) height(G)=5 CS(H) (5, 0, 0), (6, 0, 0), = (8, 4, 4), (9, 0, 0) height(H)=6 8 CS(I) (3, 3, 5), = (6, 0, 0) height(I)=5 E F G H I (8, 4, 4) CS(G) covers [E, G]. [E, F] [E, G] Add a vertex labeled with [E, G] to G 8 in the table.
An ordered term tree An ordered tree O 11 (3, 4) (5, 5) D CS(D) (3, 3, 4), = (6, 0, 0) E F CS(E) = (3, 3, 3) height(E)=3 height(D)=5 G H CS(F) 8 E F [E, F] G [E, G] H [H, H] I 7 CS(G) = (1, 0, 0), (4, 0, 0) (7, 2, 3) height(F)=2 7 I = (2, 0, 0), (4, 0, 0), (5, 0, 0), (8, 4, 4) height(G)=5 CS(H) (5, 0, 0), (6, 0, 0), = (8, 4, 4), (9, 0, 0) height(H)=6 8 CS(I) (3, 3, 5), = (6, 0, 0) height(I)=5 (8, 4, 4) CS(H) covers [H, H]. Add a directed edge from [E, F] at F 7 to [E, G] at G 8, because a vertex labeled with two. Add consecutive variables cover [H, H] to from H 8 in. Ethe table. all vertices to G.
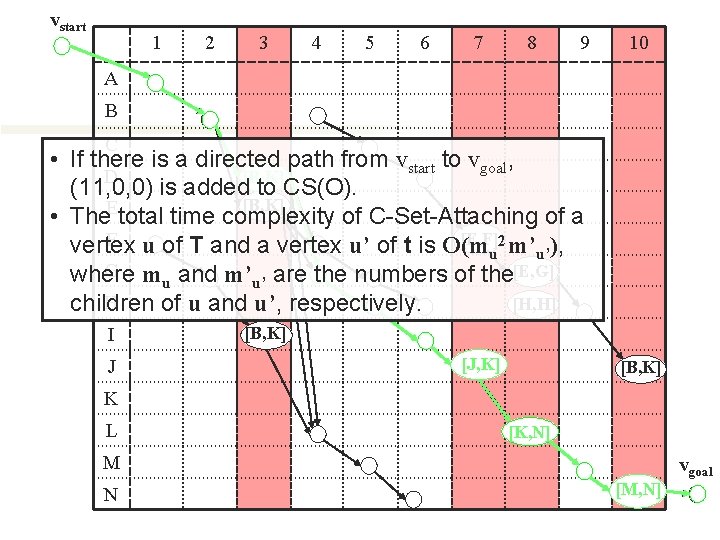
vstart 1 2 3 4 5 6 7 8 9 10 A B C • If there is a directed path from vstart to vgoal, D [B, K] (11, 0, 0) is added to CS(O). [B, K] E • The total time complexity of C-Set-Attaching of a [E, F]2 m’ ), F u of T and a vertex u’ of t is O(m vertex u u’ G m and m’ are the numbers of the[E, G] where u u’ H [H, H] children of u and u’, respectively. I J [B, K] [J, K] [B, K] K L [K, N] M N [M, N] vgoal
Total Time Complexity n n VID-Inheriting(u): O(Smu) C-Set-Attaching(u): O(mu 2 m’u’) mu: the number of children of a vertex u of T, m’u’: the number of children of a vertex u’ of t. n Total: O(N max{n. Dmax, S}) n: the number of vertices of t, N: the number of vertices of T, S: the total amount of the lowest trunk lengths of all variables of t, Dmax: the maximum number of children of a vertex of T.
Conclusions • An O(N max{n. Dmax, S}) Time Matching Algorithm for Ordered Term Trees with Height-Constrained Variables. • [Our Related Works] Polynomial-Time Learning Algorithms for Ordered Term Trees with Height. Constrained Variables [Suzuki et al. , PRICAI'04], [Matsumoto and Shoudai, ALT'04]. Future Works: • An Efficient Matching Algorithm for Ordered Term Trees with Height-Constrained Multi-Child Port Variables. • Polynomial-Time Learning Algorithms for Ordered Term Trees with Height-Constrained Multi-Child Port Variables.
Thank you for your attention.