A Physical difference between Short and Long GRBs

A Physical difference between Short and Long GRBs L. G. Balázs, Z. Bagoly, I. Horváth , A. Mészáros, and P. Mészáros 25/10/2021 GRB meeting, PSU 2004

Structure of this talk Basic properties of GRBs Analysis of the durations Analysis of the fluences Correlation between fluence and duration Conclusions 25/10/2021 GRB meeting, PSU 2004

Basic properties of GRBs Sample: Current BATSE Gamma ray Burst Catalog Measured quantities: Fluences: F 1 [25, 50]ke. V, F 2 [50, 100]ke. V, F 3 [100, 300]ke. V, F 4 [>300] ke. V, Ftot=F 1+F 2+F 3+F 4 Durations: T 90 [5%; 95%], T 50 [25%; 75%] Peak fluxes: on 64 ms, 256 ms, 1024 ms time resolution Principal Component Analysis (PCA) Two physically important quantities: 1. 2. T 90, T 50, F 1, F 2, F 3, F 4 P 64, P 256, P 1024 F Tm 25/10/2021 GRB meeting, PSU 2004

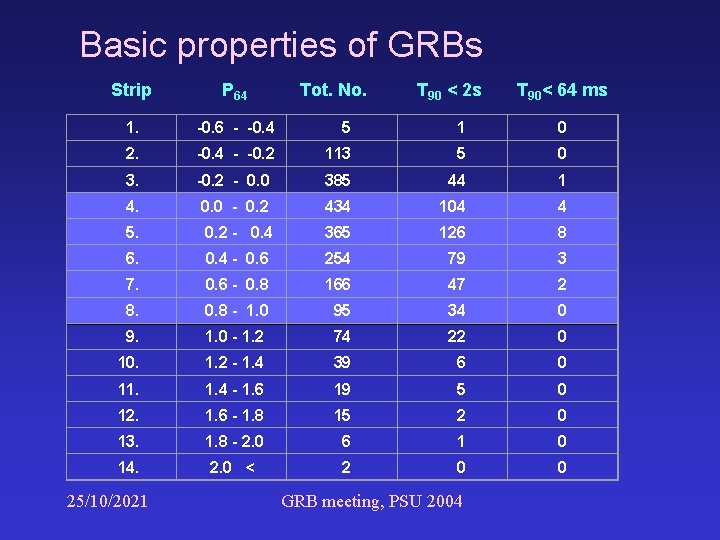
Basic properties of GRBs Strip P 64 1. -0. 6 - -0. 4 5 1 0 2. -0. 4 - -0. 2 113 5 0 3. -0. 2 - 0. 0 385 44 1 4. 0. 0 - 0. 2 434 104 4 5. 0. 2 - 0. 4 365 126 8 6. 0. 4 - 0. 6 254 79 3 7. 0. 6 - 0. 8 166 47 2 8. 0. 8 - 1. 0 95 34 0 9. 1. 0 - 1. 2 74 22 0 10. 1. 2 - 1. 4 39 6 0 11. 1. 4 - 1. 6 19 5 0 12. 1. 6 - 1. 8 15 2 0 13. 1. 8 - 2. 0 6 1 0 14. 2. 0 < 2 0 0 25/10/2021 Tot. No. T 90 < 2 s GRB meeting, PSU 2004 T 90< 64 ms

Analysis of the durations Distribution of log. T 90: Superposition of two Gaussians Consequence: distribution is intrinsic Proof: Cramer theorem log. T 90 = logt 90+logf(z) If log. T 90 is Gaussian then logt 90 and logf(z) are as well intrinsic 25/10/2021 GRB meeting, PSU 2004

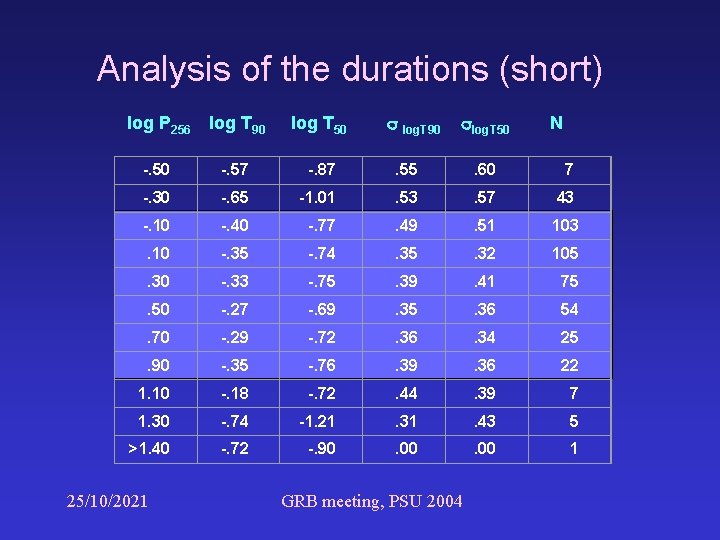
Analysis of the durations (short) log. T 90 log. T 50 log P 256 log T 90 log T 50 -. 57 -. 87 . 55 . 60 7 -. 30 -. 65 -1. 01 . 53 . 57 43 -. 10 -. 40 -. 77 . 49 . 51 103 . 10 -. 35 -. 74 . 35 . 32 105 . 30 -. 33 -. 75 . 39 . 41 75 . 50 -. 27 -. 69 . 35 . 36 54 . 70 -. 29 -. 72 . 36 . 34 25 . 90 -. 35 -. 76 . 39 . 36 22 1. 10 -. 18 -. 72 . 44 . 39 7 1. 30 -. 74 -1. 21 . 31 . 43 5 >1. 40 -. 72 -. 90 . 00 1 25/10/2021 GRB meeting, PSU 2004 N

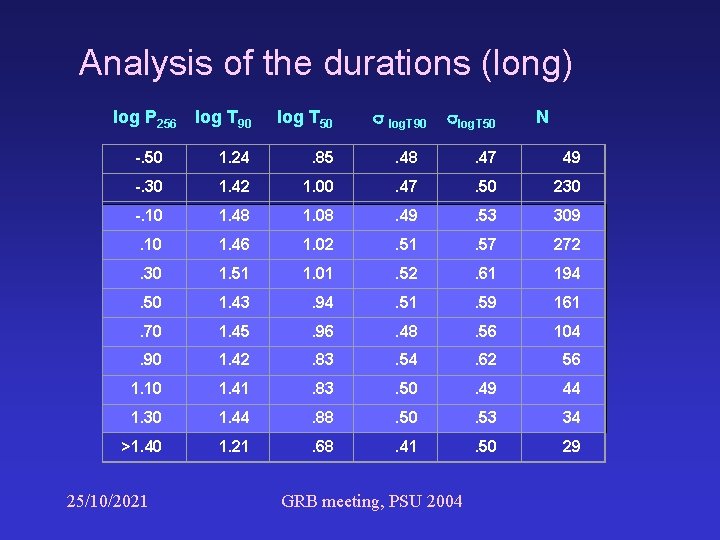
Analysis of the durations (long) log P 256 log. T 90 log. T 50 log T 90 log T 50 -. 50 1. 24 . 85 . 48 . 47 49 -. 30 1. 42 1. 00 . 47 . 50 230 -. 10 1. 48 1. 08 . 49 . 53 309 . 10 1. 46 1. 02 . 51 . 57 272 . 30 1. 51 1. 01 . 52 . 61 194 . 50 1. 43 . 94 . 51 . 59 161 . 70 1. 45 . 96 . 48 . 56 104 . 90 1. 42 . 83 . 54 . 62 56 1. 10 1. 41 . 83 . 50 . 49 44 1. 30 1. 44 . 88 . 50 . 53 34 >1. 40 1. 21 . 68 . 41 . 50 29 25/10/2021 GRB meeting, PSU 2004 N

Analysis of the fluences The observed total fluence can be written in the form: In case of short burst log Ftot is Gaussian Cramer theorem is applicable For long GRBs by direct measurements of z >50% of Ftot is intrinsic 25/10/2021 GRB meeting, PSU 2004

Correlation between fluence and duration Effect of the detection threshold Intrinsic relationship between fluence and duration ML estimation via EM algorithm Possible sources of bias 25/10/2021 GRB meeting, PSU 2004

Effect of the detection threshold According to the Law of full Probability The kernel represent intrinsic relationship G(p) is strongly influenced by the threshold 25/10/2021 GRB meeting, PSU 2004

Intrinsic relationship between fluence and duration From PCA two important quantities: Duration and peak flux is a noise term fixing p - power law relationship between Ftot and T 90 25/10/2021 GRB meeting, PSU 2004

ML estimation via EM algorithm Fitting function: superposition of two 2 D Gaussians 25/10/2021 GRB meeting, PSU 2004

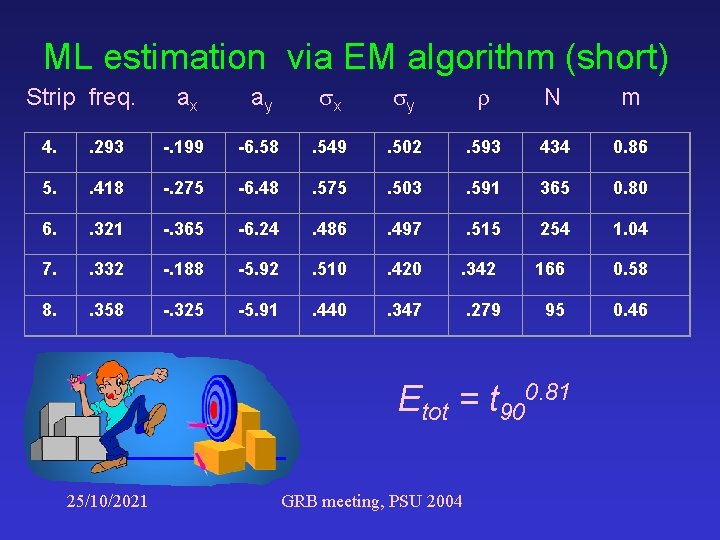
ML estimation via EM algorithm (short) Strip freq. ax ay x y N m 4. . 293 -. 199 -6. 58 . 549 . 502 . 593 434 0. 86 5. . 418 -. 275 -6. 48 . 575 . 503 . 591 365 0. 80 6. . 321 -. 365 -6. 24 . 486 . 497 . 515 254 1. 04 7. . 332 -. 188 -5. 92 . 510 . 420 . 342 166 0. 58 8. . 358 -. 325 -5. 91 . 440 . 347 . 279 95 0. 46 Etot = t 900. 81 25/10/2021 GRB meeting, PSU 2004

ML estimation via EM algorithm (long) freq. ax ay x y N m 4. . 707 1. 56 -5. 48 . 400 . 434 . 586 434 1. 15 5. . 582 1. 61 -5. 23 . 445 . 463 . 599 365 1. 07 6. . 679 1. 41 -5. 21 . 538 . 613 . 753 254 1. 19 7. . 668 1. 46 -4. 89 . 448 . 459 . 610 166 1. 04 8. . 642 1. 39 -4. 77 . 541 . 531 . 656 95 . 97 Strip Etot = t 901. 11 25/10/2021 GRB meeting, PSU 2004

4. ML estimation via EM algorithm 5. 8. 6. 7. 25/10/2021 GRB meeting, PSU 2004

Possible sources of bias Effect of the threshold True vs. observed fluence Bias from the spectral response Bias from the finite time resolution 25/10/2021 GRB meeting, PSU 2004

Effect of the threshold Direct effect on the form of G(p): Three time scales (64 ms, 256 ms. 1025 ms) No sharp cut. Indirect effect: on T 90 and Ftot Influence on P(log. T 90, log. Ftot) mainly through G(p) 25/10/2021 GRB meeting, PSU 2004

True vs. observed fluence Observed light curve: „iceberg” effect in duration and fluence Possible effect on the shape of P(Ftot, T 90): Long GRBs: no gradual changes in the shape Short GRBs: gradual changes 25/10/2021 GRB meeting, PSU 2004

Bias from the spectral response Short GRBs are harder apparent positive correlation with duration assuming no intrinsic correlation The spectral bias is more serious at faint GRBs Short GRBs gradual decrease of slope Long GRBs no significant change in Strips 4. -8. 25/10/2021 GRB meeting, PSU 2004

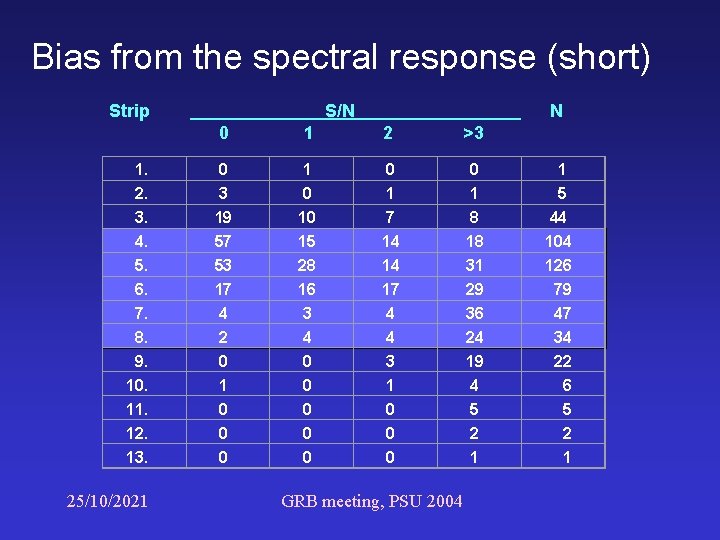
Bias from the spectral response (short) Strip 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 25/10/2021 S/N N 0 1 2 >3 0 3 19 57 53 17 4 2 0 1 0 0 0 10 15 28 16 3 4 0 0 0 1 7 14 14 17 4 4 3 1 0 0 1 8 18 31 29 36 24 19 4 5 2 1 GRB meeting, PSU 2004 1 5 44 104 126 79 47 34 22 6 5 2 1

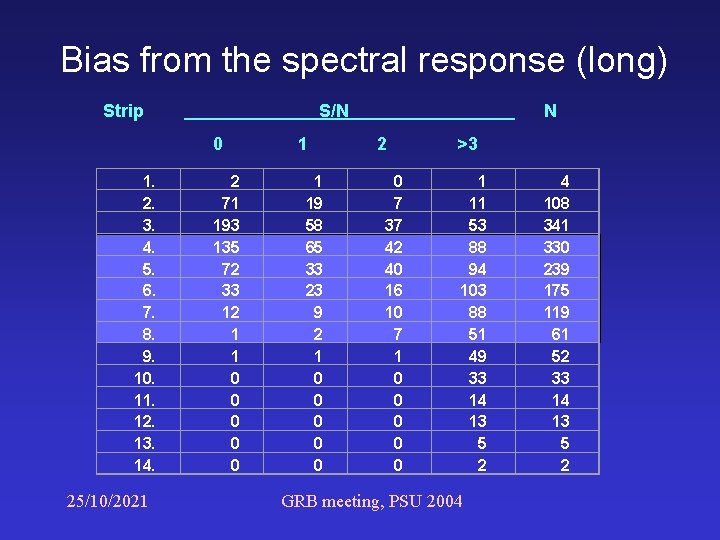
Bias from the spectral response (long) Strip S/N 0 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 25/10/2021 2 71 193 135 72 33 12 1 1 0 0 0 1 1 19 58 65 33 23 9 2 1 0 0 0 N 2 0 7 37 42 40 16 10 7 1 0 0 0 >3 1 11 53 88 94 103 88 51 49 33 14 13 5 2 GRB meeting, PSU 2004 4 108 341 330 239 175 119 61 52 33 14 13 5 2

Bias from the finite time resolution If T 90 < 64 ms no correlation with Ftot Peak flux is computed from the same bin as Ftot As T 90 increases – increasing no of 64 ms bins We compared the variances and covariances within and between bins Results of Multivariate Analysis of variance (MANOVA) : 1 st bin differs at 99. 5% sig. level 25/10/2021 GRB meeting, PSU 2004

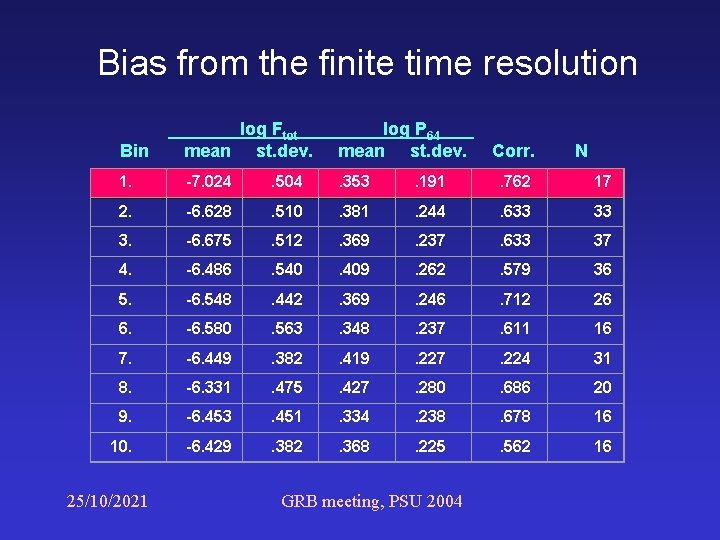
Bias from the finite time resolution Bin log Ftot mean st. dev. log P 64 mean st. dev. 1. -7. 024 . 504 . 353 . 191 . 762 17 2. -6. 628 . 510 . 381 . 244 . 633 33 3. -6. 675 . 512 . 369 . 237 . 633 37 4. -6. 486 . 540 . 409 . 262 . 579 36 5. -6. 548 . 442 . 369 . 246 . 712 26 6. -6. 580 . 563 . 348 . 237 . 611 16 7. -6. 449 . 382 . 419 . 227 . 224 31 8. -6. 331 . 475 . 427 . 280 . 686 20 9. -6. 453 . 451 . 334 . 238 . 678 16 10. -6. 429 . 382 . 368 . 225 . 562 16 25/10/2021 GRB meeting, PSU 2004 Corr. N

Conclusions • there is a power law relation between the fluence and duration • this relation is significantly different for the two groups • values of exponents were obtained, 0. 81 (short) and 1. 11 (long) • difference is significant on the 4. 7 level. The result is completely model independent based on Cramer theorem and Law of full Probability 25/10/2021 GRB meeting, PSU 2004

25/10/2021 GRB meeting, PSU 2004