A perfect square is a number whose product

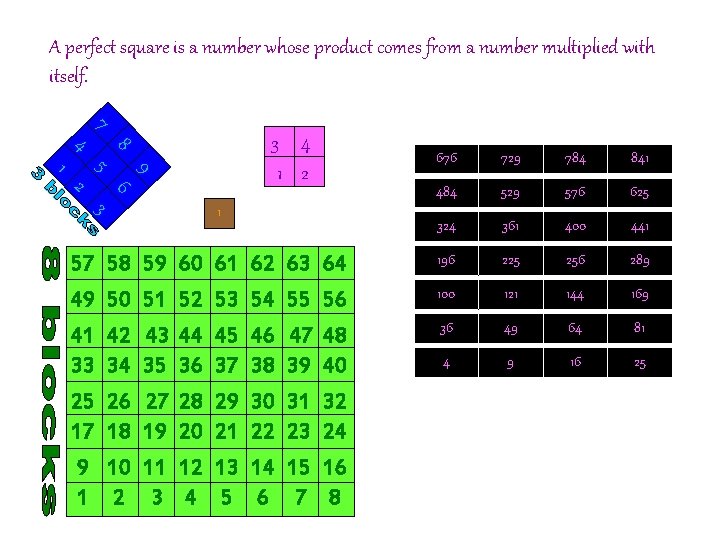
A perfect square is a number whose product comes from a number multiplied with itself. 7 8 4 9 5 1 3 4 1 2 729 784 841 484 529 576 625 324 361 400 441 62 63 64 196 225 256 289 54 46 38 30 22 14 6 100 121 144 169 36 49 64 81 4 9 16 25 6 2 676 3 1 57 58 59 60 61 49 50 51 52 53 41 42 43 44 45 33 34 35 36 37 25 26 27 28 29 17 18 19 20 21 9 10 11 12 13 1 2 3 4 5 55 47 39 31 23 15 7 56 48 40 32 24 16 8

A perfect square is a number that has a rational square root. 49 is a perfect square because 361 is a perfect square because 2. 25 is a perfect square because 0. 01 is a perfect square because 48 is NOT a perfect square because 10 is NOT a perfect square because 2. 24 is NOT a perfect square because

A variable perfect square is a variable that has a square root. This happens whenever the exponent attached to the variable is even. x 2 is a perfect square because a 6 is a perfect square because z 16 is a perfect square because x is a NOT perfect square because its exponent is odd x 3 is a NOT perfect square because its exponent is odd x 9 is a NOT perfect square because its exponent is odd

We can combine the concepts of perfect square numbers with perfect square variables.

Recognizing perfect squares is a very important element when factoring using Difference of 2 Squares. However, there are two other distinguishing features both of which are indicated in the title. Difference of 2 Squares - terms must be perfect squares. - must involve subtraction. In essence both terms must have opposite signs (one positive and the other negative). - there must be two terms. No more. No less. EXAMPLE: 25 x 2 - 49 - Both terms are perfect squares. - Terms are being subtracted. - There are two terms.

The trickiest thing about this method is the recognition factor. All three elements must be verified before the expression is factored using Difference of 2 Squares. Identify whether the following polynomials can be factored using Difference of 2 Squares or not. 1. 4 p 2 – 9 q 2 _______ 2. 100 – a 6 _______ 3. x 2 – 9 x _______ 4. a 10 – 10 _______ For those that can’t be factored using Difference of 2 Squares what prevents it from being factored that way? 5. t 100 – 100 _______ 6. 2 m 2 – 50 _______ 7. -121 s 4 + 196 p 8 _______ 11. 16 p 2 + 9 q 2 _______ 8. d 9 – 49 e 16 _______ 12. –a 2 – 36 _______ 9. y 6 – 1 10. _______

After it is determined that an expression can be factored using Difference of 2 Squares, all that is left is to determine what the factors actually are. The factors of this kind of polynomial will be a binomial with its conjugate. The binomial is basically the sum of the square roots of each term. The conjugate is therefore the difference of the square roots of each term. EXAMPLE: 25 x 2 - 49 =(5 x + 7) To verify: (5 x - 7) (5 x + 7) (5 x - 7) = 25 x 2 - 35 x = 25 x 2 - 49 + 35 x - 49

1. 4 p 2 – 9 q 2 = (2 p + 3 q)(2 p – 3 q) 2. 100 – a 6 = (10 + a 3)(10 – a 3) 3. x 2 – 9 x = x(x – 9) 4. a 10 – 10 Can not be factored because 10 is not a perfert square. 5. t 100 – 100 = (t 50 + 10)(t 50 – 10) 6. 2 m 2 – 50 = 2(m 2 - 25) 7. -121 s 4 + 196 p 8 8. d 9 – 49 e 16 9. y 6 – 1 = 2(m + 5)(m – 5) = 196 p 8 – 121 s 4 = (14 p 4 + 11 s 2)(14 p 4 - 11 s 2) Can not be factored because d 9 is not a perfert square. = (y 3 + 1)(y 3 – 1) 10. 11. 16 p 2 + 9 q 2 12. –a 2 – 36 Can not factor SUM of 2 Squares = -1(a 2 + 36) Can not factor SUM of 2 Squares