a Part 1 MatterAntimatter Asymmetry Part 2 CP

a Part 1: Matter-Antimatter Asymmetry Part 2: CP Violation and the SM g b Part 3: Beyond the Standard Model New Results from the Ba. Bar Experiment K. Honscheid Dept. of Physics Ohio University K. Honscheid, WSU Apr. State 15, 2005

Matter, Energy and the Big Bang • Einstein showed us that matter and energy are equivalent • When matter and antimatter meet, they annihilate into energy • Energy can also materialize as particle-antiparticle pair Predict: Exp: n. Matter/n. Photon~ 0 nb/ng~ (6. 1 +/- 0. 3) x 10 -10 (WMAP) K. Honscheid, WSU Apr. 15, 2005

So how can this happen? In 1967, A. Sakharov showed that the generation of the net baryon number in the universe requires: 1. Baryon number violation (Proton Decay) 2. Thermal non-equilibrium 3. C and CP violation (Asymmetry between particle and anti-particle) Transition to broken electroweak symmetry provides these conditions K. Honscheid, WSU Apr. 15, 2005

Experimental Possibilities: • Get equal amounts of matter and anti-matter • Wait… • See what’s left (in anything) K. Honscheid, WSU Apr. 15, 2005

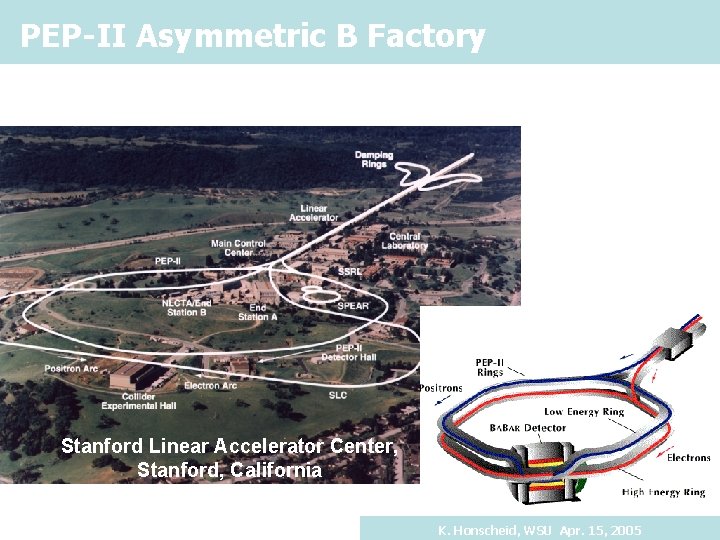
PEP-II Asymmetric B Factory Stanford Linear Accelerator Center, Stanford, California K. Honscheid, WSU Apr. 15, 2005

The Ba. Bar Experiment K. Honscheid, WSU Apr. 15, 2005

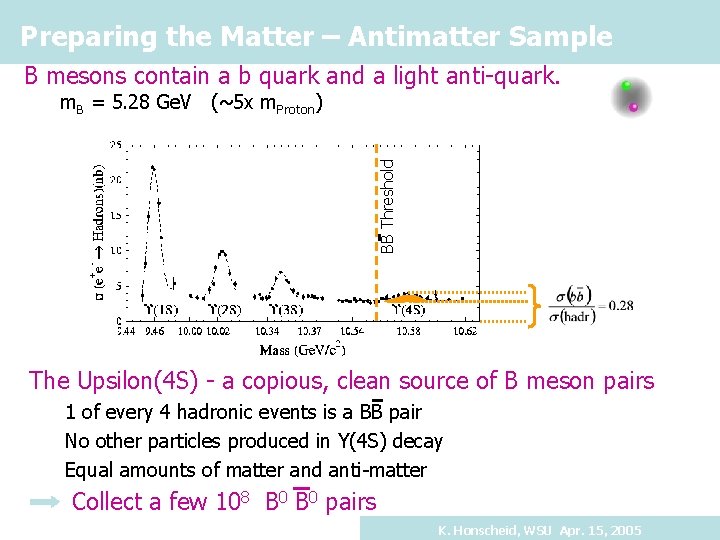
Preparing the Matter – Antimatter Sample B mesons contain a b quark and a light anti-quark. BB Threshold m. B = 5. 28 Ge. V (~5 x m. Proton) The Upsilon(4 S) - a copious, clean source of B meson pairs 1 of every 4 hadronic events is a BB pair No other particles produced in Y(4 S) decay Equal amounts of matter and anti-matter Collect a few 108 B 0 pairs K. Honscheid, WSU Apr. 15, 2005

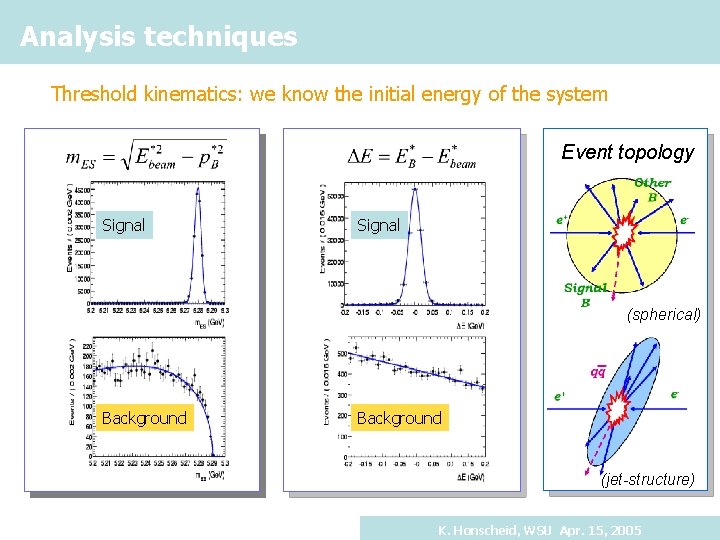
Analysis techniques Threshold kinematics: we know the initial energy of the system Event topology Signal (spherical) Background (jet-structure) K. Honscheid, WSU Apr. 15, 2005

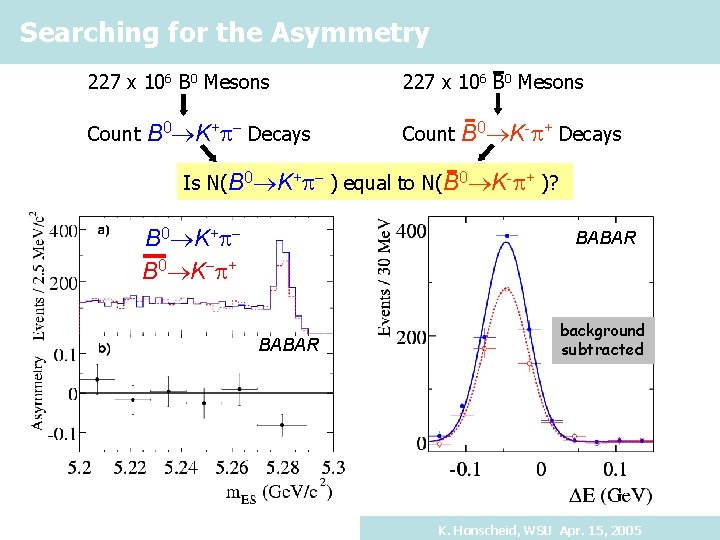
Searching for the Asymmetry 227 x 106 B 0 Mesons Count B 0 K+ Decays 227 x 106 B 0 Mesons Count B 0 K- + Decays Is N(B 0 K+ ) equal to N(B 0 K- + )? K. Honscheid, WSU Apr. 15, 2005

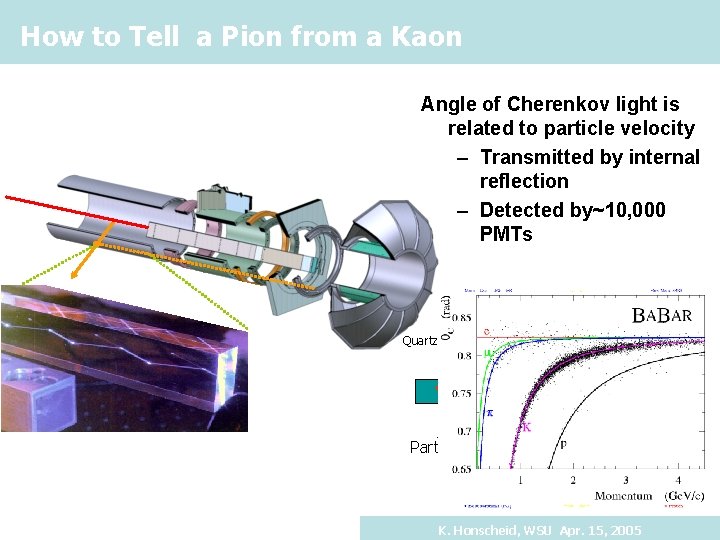
How to Tell a Pion from a Kaon Angle of Cherenkov light is related to particle velocity – Transmitted by internal reflection – Detected by~10, 000 PMTs Quartz bar Particle Active Detector Surface Cherenkov light K. Honscheid, WSU Apr. 15, 2005

Searching for the Asymmetry 227 x 106 B 0 Mesons Count B 0 K+ Decays 227 x 106 B 0 Mesons Count B 0 K- + Decays Is N(B 0 K+ ) equal to N(B 0 K- + )? B 0 K+ B 0 K + BABAR background subtracted K. Honscheid, WSU Apr. 15, 2005

Direct CP Violation in B Decays Using We obtain First confirmed observation of direct CP violation in B decays K. Honscheid, WSU Apr. 15, 2005

Part 2: CP Violation in the Standard Model CP Operator: CP( g q coupling q’ J ) = q’ g* q J Mirror To incorporate CP violation g ≠ g* (coupling has to be complex) K. Honscheid, WSU Apr. 15, 2005

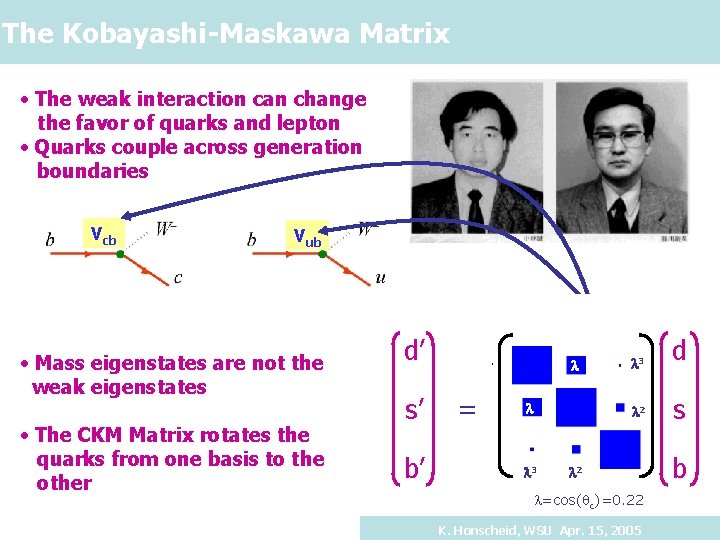
The Kobayashi-Maskawa Matrix • The weak interaction can change the favor of quarks and lepton • Quarks couple across generation boundaries Vcb Vub • Mass eigenstates are not the weak eigenstates • The CKM Matrix rotates the quarks from one basis to the other d’ s’ b’ d u s b Vud Vlus Vub d l 3 = c Vcdl Vcs Vcbl 2 t Vtdl Vltd Vtb 3 2 l=cos(qc)=0. 22 K. Honscheid, WSU Apr. 15, 2005 s b

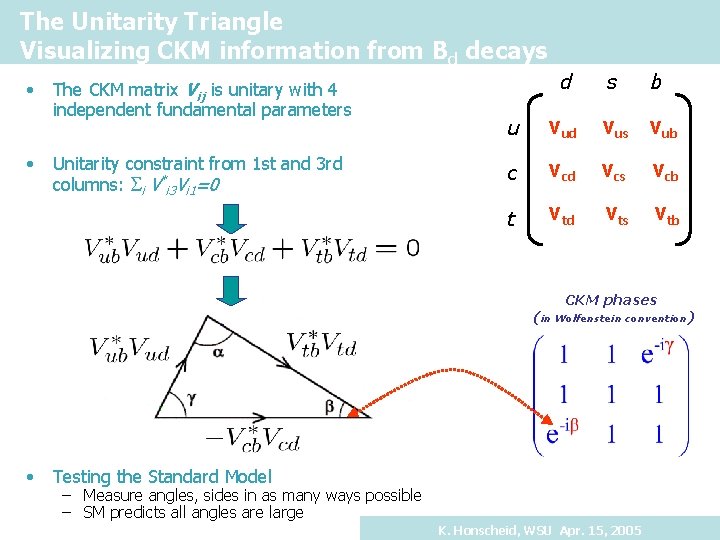
The Unitarity Triangle Visualizing CKM information from Bd decays • • The CKM matrix Vij is unitary with 4 independent fundamental parameters Unitarity constraint from 1 st and 3 rd columns: i V*i 3 Vi 1=0 d s b u Vud Vus Vub c Vcd Vcs Vcb t Vtd Vts Vtb CKM phases (in Wolfenstein convention) • Testing the Standard Model – Measure angles, sides in as many ways possible – SM predicts all angles are large K. Honscheid, WSU Apr. 15, 2005

Understanding CP Violation in B Kp Tree decay B 0 K -p + K+ p - A 1 = a 1 eifif 11 eid 1 g + A 2 = a 2 eif 2 eid 2 A 1 = a 1 e-if-if 11 eid 1 Penguin decay + A 2 = a 2 e-if 2 eid 2 • include the strong phase (doesn’t change sign) • more than one amplitude with different weak phase; (A = A 1+A 2) |A|2 – |A|2 G(B) – G(B) ~2 sin(f 1 = 0 Asymmetry = = 2 2 |A| + |A| G(B) + G(B) f 2) sin(d 1 - d 2) K. Honscheid, WSU Apr. 15, 2005

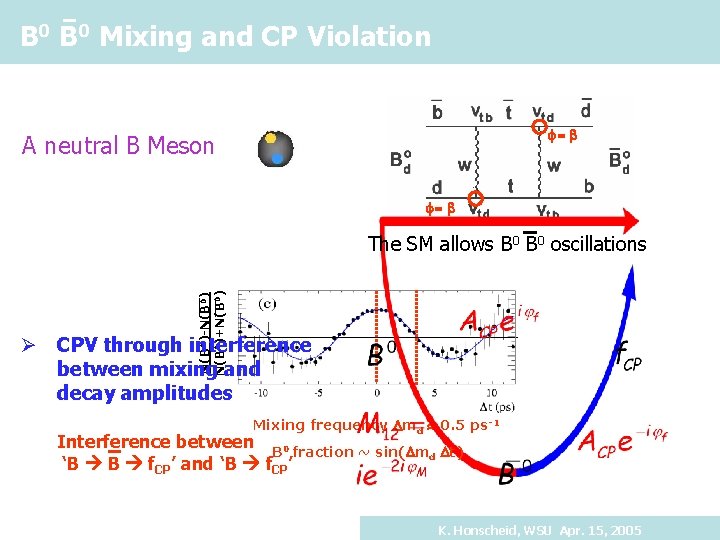
B 0 Mixing and CP Violation f=b A neutral B Meson f=b N(B 0)-N(B 0)+N(B 0) The SM allows B 0 oscillations Ø CPV through interference between mixing and decay amplitudes Mixing frequency Dmd 0. 5 ps-1 Interference between B 0 fraction ~ sin(Dm Dt) d ‘B B f. CP’ and ‘B f. CP’ K. Honscheid, WSU Apr. 15, 2005

Time-Dependent CP Asymmetries b W+ B 0 c c CP Eigenstate: h. CP = -1 s d d Amplitude of CP asymmetry Quark subprocess B 0 mixing K. Honscheid, WSU Apr. 15, 2005

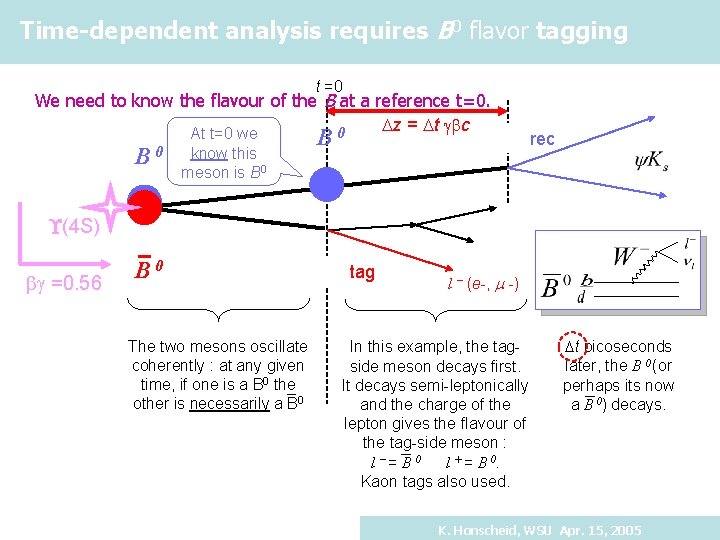
Time-dependent analysis requires B 0 flavor tagging t =0 We need to know the flavour of the B at a reference t=0. Dz = Dt gbc 0 At t=0 we B 0 know this meson is B 0 B rec (4 S) bg =0. 56 B 0 The two mesons oscillate coherently : at any given time, if one is a B 0 the other is necessarily a B 0 tag l (e-, m -) In this example, the tagside meson decays first. It decays semi-leptonically and the charge of the lepton gives the flavour of the tag-side meson : l = B 0 l + = B 0. Kaon tags also used. Dt picoseconds later, the B 0 (or perhaps its now a B 0) decays. K. Honscheid, WSU Apr. 15, 2005

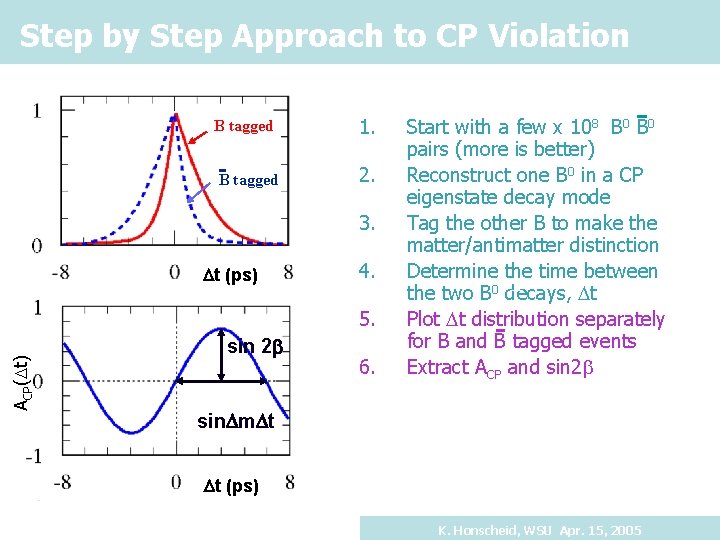
Step by Step Approach to CP Violation B tagged 1. B tagged 2. 3. Dt (ps) 4. ACP(Dt) 5. sin 2 b 6. Start with a few x 108 B 0 pairs (more is better) Reconstruct one B 0 in a CP eigenstate decay mode Tag the other B to make the matter/antimatter distinction Determine the time between the two B 0 decays, Dt Plot Dt distribution separately for B and B tagged events Extract ACP and sin 2 b sin. Dm. Dt Dt (ps) K. Honscheid, WSU Apr. 15, 2005

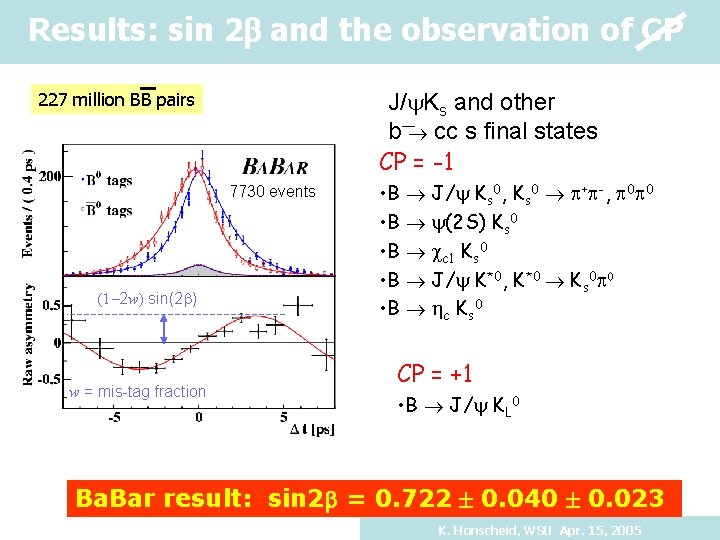
Results: sin 2 b and the observation of CP 227 million BB pairs J/ Ks and other b cc s final states CP = -1 7730 events (1 -2 w) sin(2 b) w = mis-tag fraction • B J/ Ks 0, Ks 0 + -, 0 0 • B (2 S) Ks 0 • B c 1 Ks 0 • B J/ K*0, K*0 Ks 0 • B c Ks 0 CP = +1 • B J/ KL 0 Ba. Bar result: sin 2 b = 0. 722 0. 040 0. 023 K. Honscheid, WSU Apr. 15, 2005

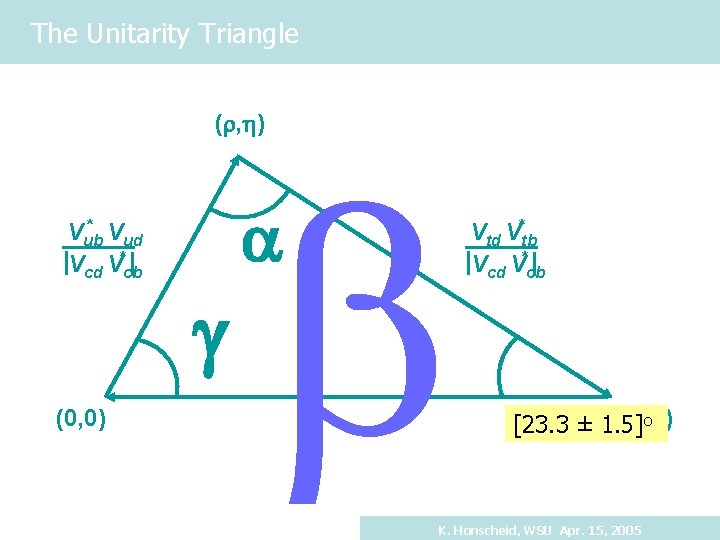
The Unitarity Triangle (r, h) * Vub Vud Vcd V*cb (0, 0) b a g Vtd V*tb Vcd V*cb o (0, 1) [23. 3 ± 1. 5] K. Honscheid, WSU Apr. 15, 2005

y. Ks is not the only CP Eigenstate Access to from the interference of a b→u decay (g) with B 0 B 0 mixing (b) B 0 B 0 mixing Tree decay g = b g sin 2 a ACP(t)=sin(2 )sin(Dmd. Dt). K. Honscheid, WSU Apr. 15, 2005

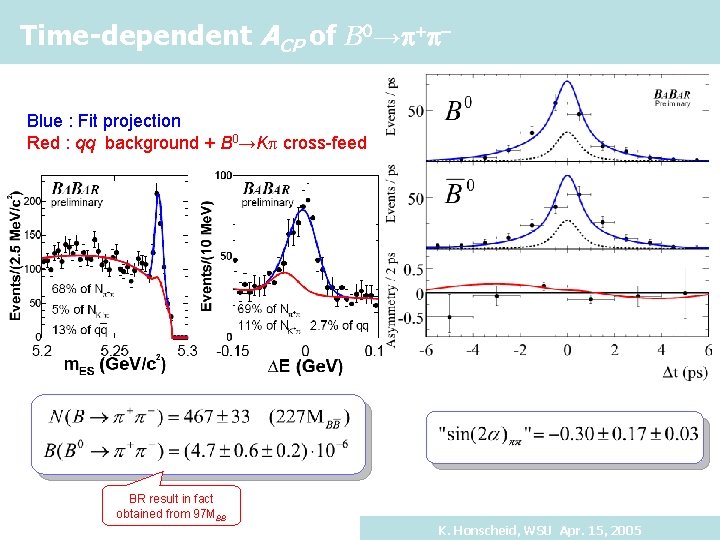
Time-dependent ACP of B 0→p+p. Blue : Fit projection Red : qq background + B 0→K cross-feed BR result in fact obtained from 97 MBB K. Honscheid, WSU Apr. 15, 2005

Houston, we have a problem B 0 + K K K B 0 K + - q q B 0 + 157 19 (4. 7 0. 6 0. 2) x 10 -6 B 0 K+ 589 30 (17. 9 0. 7) x 10 -6 Penguin/Tree ~ 30% K. Honscheid, WSU Apr. 15, 2005

The route to sin(2 a): Penguin Pollution • Access to from the interference of a b→u decay (g) with B 0 B 0 mixing (b) B 0 B 0 mixing Tree decay Penguin decay g Inc. penguin contribution How can we obtain α from αeff ? Time-dep. asymmetry : NB : T = "tree" amplitude P = "penguin" amplitude K. Honscheid, WSU Apr. 15, 2005

How to estimate |a-aeff| : Isospin analysis • Use SU(2) to relate decay rates of different hh final states (h { , r}) • Need to measure several related B. F. s | | eff 2 Difficult to reconstruct. Limiting factor in analysis Gronau, London : PRL 65, 3381 (1990) K. Honscheid, WSU Apr. 15, 2005

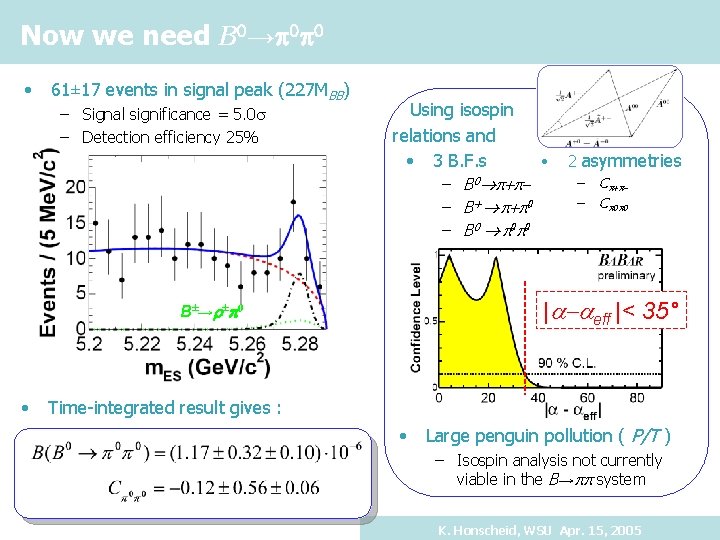
Now we need B 0→p 0 p 0 • 61± 17 events in signal peak (227 MBB) – Signal significance = 5. 0 s – Detection efficiency 25% Using isospin relations and • 3 B. F. s – B 0 p+p– B+ p+p 0 – B 0 p 0 p 0 2 asymmetries – – Cp+p. Cp 0 p 0 |a-aeff |< 35° B±→r±p 0 • • Time-integrated result gives : • Large penguin pollution ( P/T ) – Isospin analysis not currently viable in the B→pp system K. Honscheid, WSU Apr. 15, 2005

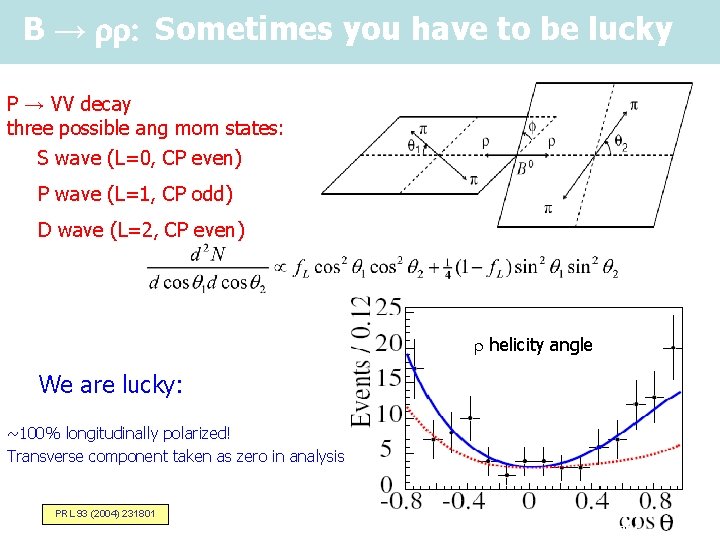
B → rr: Sometimes you have to be lucky P → VV decay three possible ang mom states: S wave (L=0, CP even) P wave (L=1, CP odd) D wave (L=2, CP even) r helicity angle We are lucky: ~100% longitudinally polarized! Transverse component taken as zero in analysis PRL 93 (2004) 231801 K. Honscheid, WSU Apr. 15, 2005

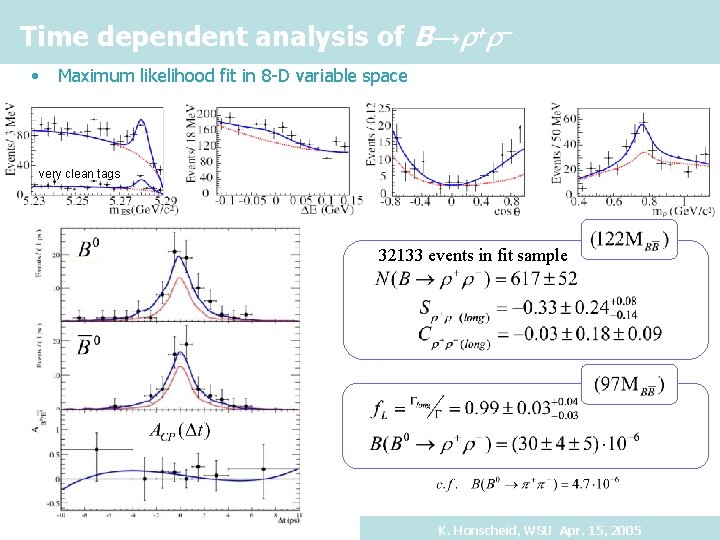
Time dependent analysis of B→r+r • Maximum likelihood fit in 8 -D variable space very clean tags 32133 events in fit sample K. Honscheid, WSU Apr. 15, 2005

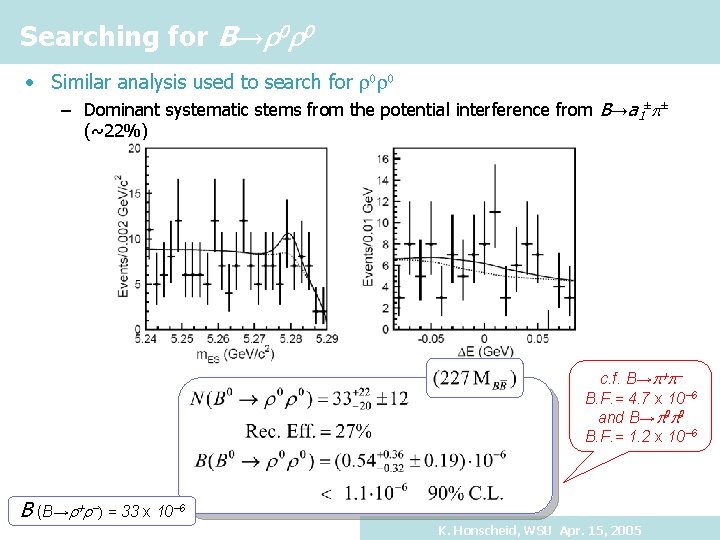
Searching for B→r 0 r 0 • Similar analysis used to search for r r – Dominant systematic stems from the potential interference from B→a 1±p± (~22%) c. f. B→p+p. B. F. = 4. 7 x 10 -6 and B→p 0 p 0 B. F. = 1. 2 x 10 -6 B (B→r+r-) = 33 x 10 -6 K. Honscheid, WSU Apr. 15, 2005

Isospin analysis using B→rr • The small rate of – |a-aeff | is small[er] means – P/T is small in the B→rr system (…Relative to B→pp system) – No isospin violation (~1%) – No EW Penguins (~2%) |a-aeff |< 11° K. Honscheid, WSU Apr. 15, 2005

The Unitarity Triangle [103 (r, h) ± 11]o * Vub Vud Vcd V*cb (0, 0) g Vtd V*tb Vcd V*cb b [23. 3 ±(0, 1) 1. 5]o K. Honscheid, WSU Apr. 15, 2005

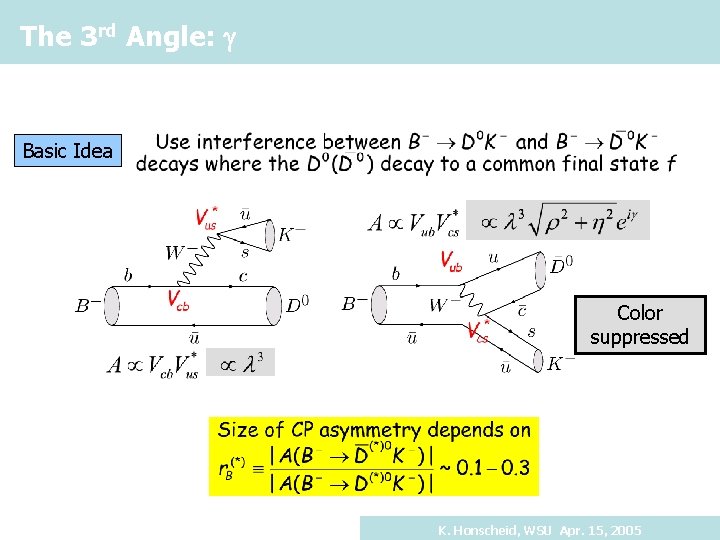
The 3 rd Angle: g Basic Idea Color suppressed K. Honscheid, WSU Apr. 15, 2005

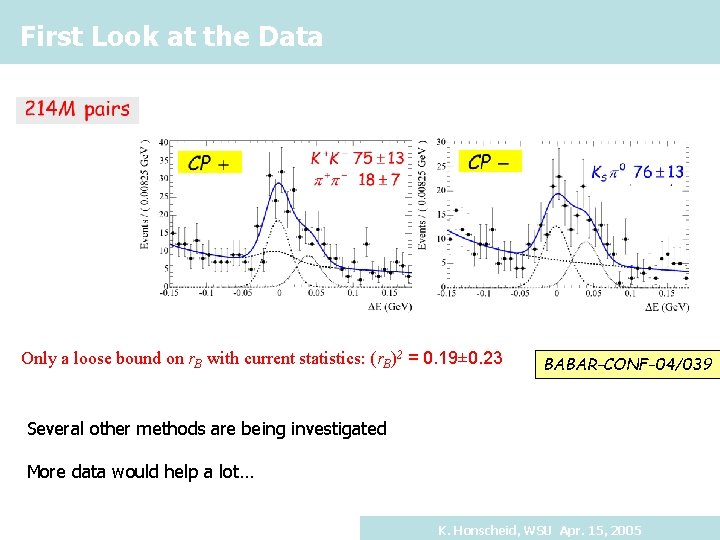
First Look at the Data Only a loose bound on r. B with current statistics: (r. B)2 = 0. 19± 0. 23 BABAR-CONF-04/039 Several other methods are being investigated More data would help a lot… K. Honscheid, WSU Apr. 15, 2005

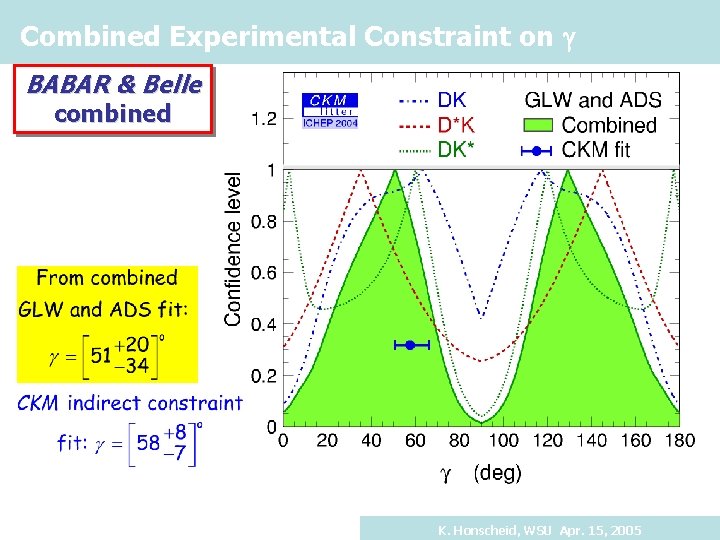
Combined Experimental Constraint on g BABAR & Belle combined K. Honscheid, WSU Apr. 15, 2005

The Unitarity Triangle g [103 ± 11]o * Vub Vud Vcd V*cb (0, 0) +20 ]o [51 -34 a Vtd V*tb Vcd V*cb b [23. 3 ± 1. 5]o K. Honscheid, WSU Apr. 15, 2005

Putting it all together • The complex phase in the CKM matrix correctly describes CPV in the B meson system. • Based on SM CPV the baryon to photon ratio in the universe should be nb/ng~ 10 -20 • Experimentally we find nb/ng~ (6. 1± 0. 3) x 10 -10 (WMAP) r K. Honscheid, WSU Apr. 15, 2005

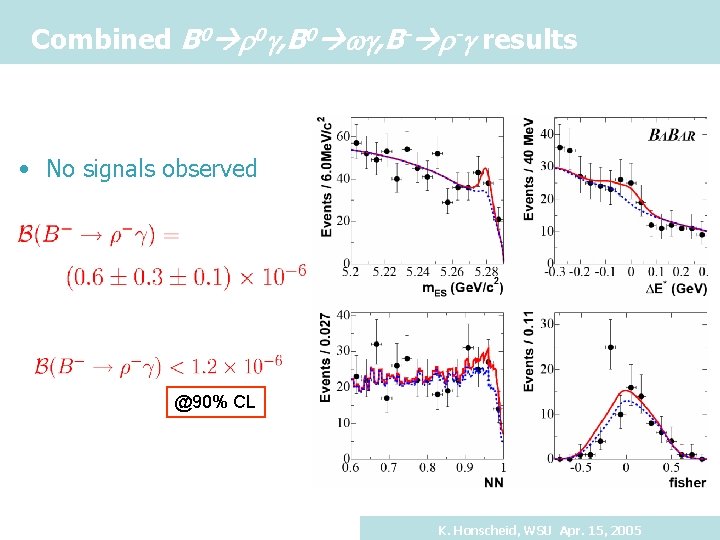
Part 3: Beyond Consistency the Standard Checks Model • FCNC transitions b sg and b dg are sensitive probes of new physics • Precise Standard Model predictions. Ali et al hep-ph/0405075 • Experimental challenges for b dg (B rg B wg) – Continuum background – Background from b sg (B K*g) (50 -100 x bigger) K. Honscheid, WSU Apr. 15, 2005

Combined B 0 r 0 g, B 0 wg, B- r-g results • No signals observed @90% CL K. Honscheid, WSU Apr. 15, 2005

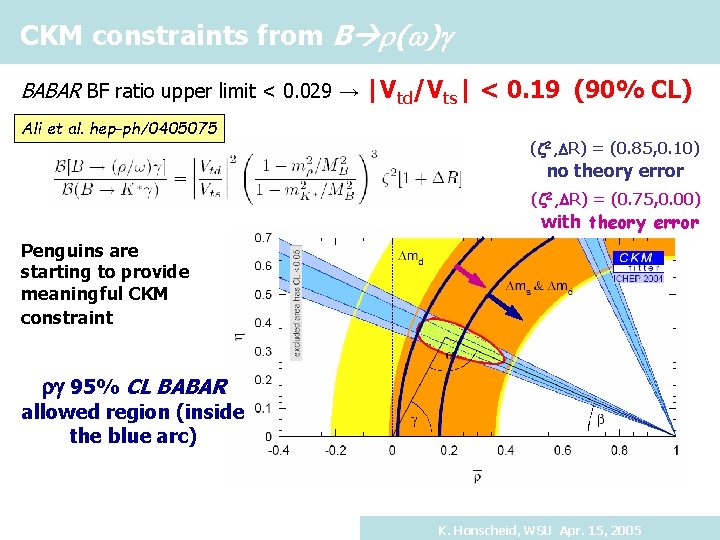
CKM constraints from B r(w)g BABAR BF ratio upper limit < 0. 029 → |Vtd/Vts| < 0. 19 (90% CL) Ali et al. hep-ph/0405075 (z 2, DR) = (0. 85, 0. 10) no theory error (z 2, DR) = (0. 75, 0. 00) with theory error Penguins are starting to provide meaningful CKM constraint rg 95% CL BABAR allowed region (inside the blue arc) K. Honscheid, WSU Apr. 15, 2005

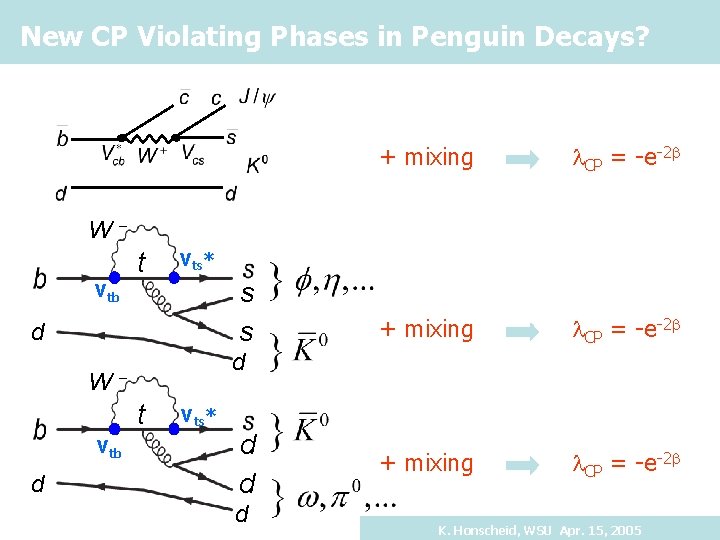
New CP Violating Phases in Penguin Decays? + mixing l. CP = -e-2 b W- t Vts* s s Vtb d W d - t Vtb d Vts* d d d K. Honscheid, WSU Apr. 15, 2005

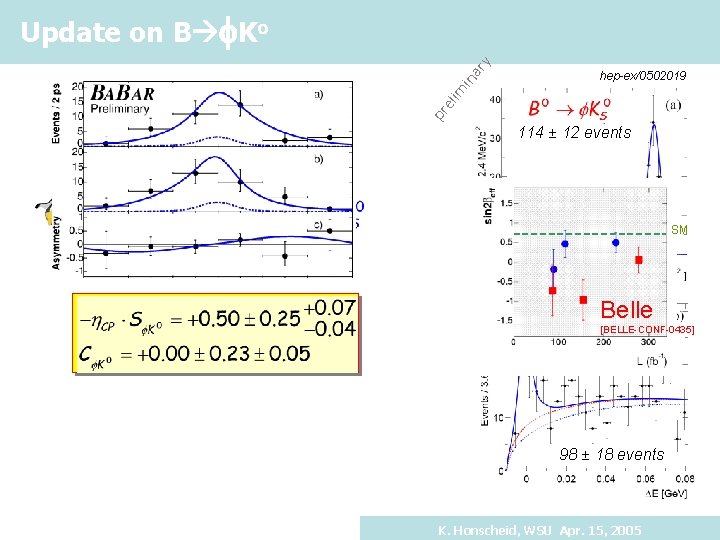
hep-ex/0502019 pr el im in a ry Update on B f. Ko 114 ± 12 events SM Belle [BELLE-CONF-0435] 98 ± 18 events K. Honscheid, WSU Apr. 15, 2005

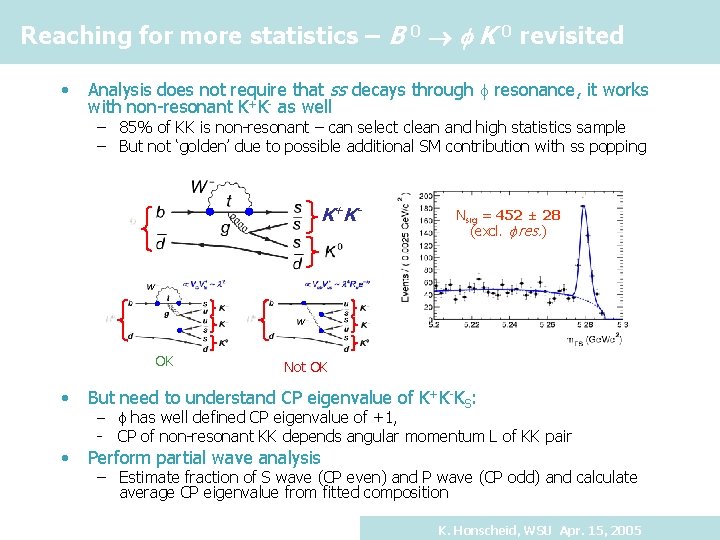
Reaching for more statistics – B 0 K 0 revisited • Analysis does not require that ss decays through f resonance, it works with non-resonant K+K- as well – 85% of KK is non-resonant – can select clean and high statistics sample – But not ‘golden’ due to possible additional SM contribution with ss popping K+ K- OK Nsig = 452 ± 28 (excl. res. ) Not OK • But need to understand CP eigenvalue of K+K-KS: • Perform partial wave analysis f has well defined CP eigenvalue of +1, - CP of non-resonant KK depends angular momentum L of KK pair – Estimate fraction of S wave (CP even) and P wave (CP odd) and calculate average CP eigenvalue from fitted composition K. Honscheid, WSU Apr. 15, 2005

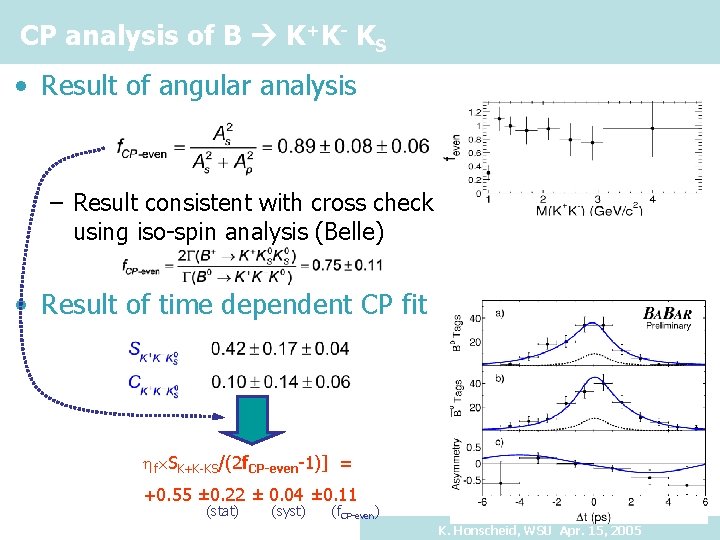
CP analysis of B K+K- KS • Result of angular analysis – Result consistent with cross check using iso-spin analysis (Belle) • Result of time dependent CP fit f SK+K-KS/(2 f. CP-even-1)] = +0. 55 ± 0. 22 ± 0. 04 ± 0. 11 (stat) (syst) (f. CP-even) K. Honscheid, WSU Apr. 15, 2005

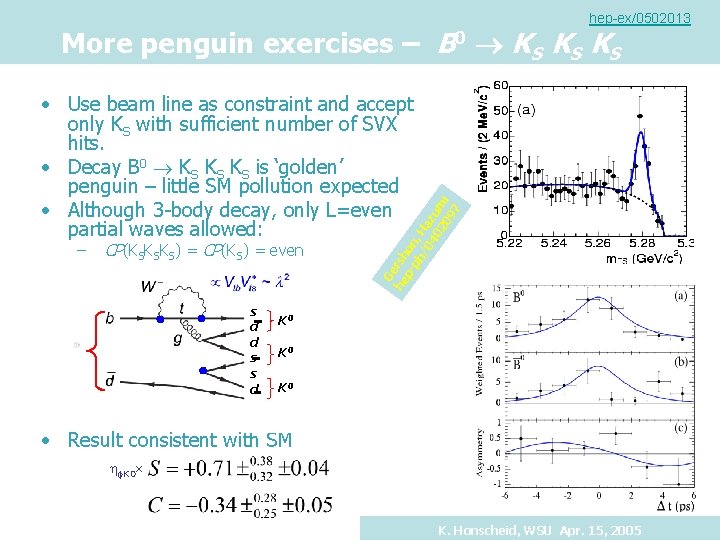
hep-ex/0502013 More penguin exercises – B 0 KS KS KS – CP(KSKSKS) = CP(KS) = even s d d s s d Ge he rsh p- on ph , H /0 a 40 zu 20 mi 97 • Use beam line as constraint and accept only KS with sufficient number of SVX hits. • Decay B 0 KS KS KS is ‘golden’ penguin – little SM pollution expected • Although 3 -body decay, only L=even partial waves allowed: K 0 K 0 • Result consistent with SM f. K 0 K. Honscheid, WSU Apr. 15, 2005

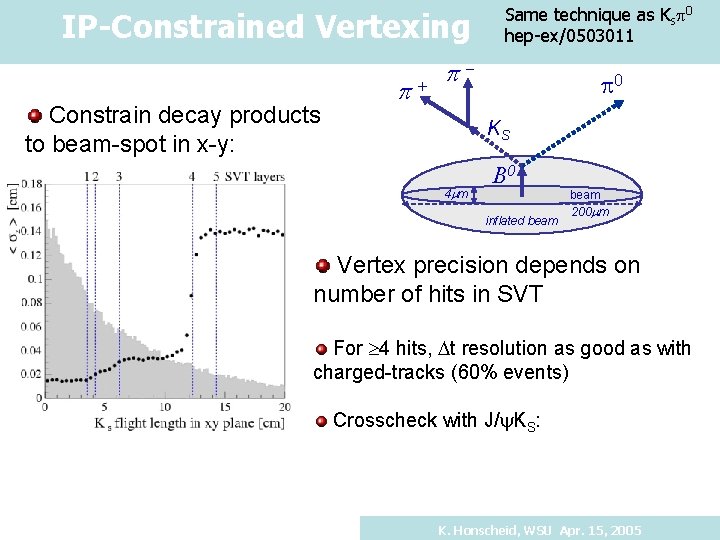
IP-Constrained Vertexing Constrain decay products to beam-spot in x-y: p+ Same technique as Ks 0 hep-ex/0503011 p- 0 KS 4 mm B 0 inflated beam 200 mm Vertex precision depends on number of hits in SVT For 4 hits, Dt resolution as good as with charged-tracks (60% events) Crosscheck with J/ KS: K. Honscheid, WSU Apr. 15, 2005

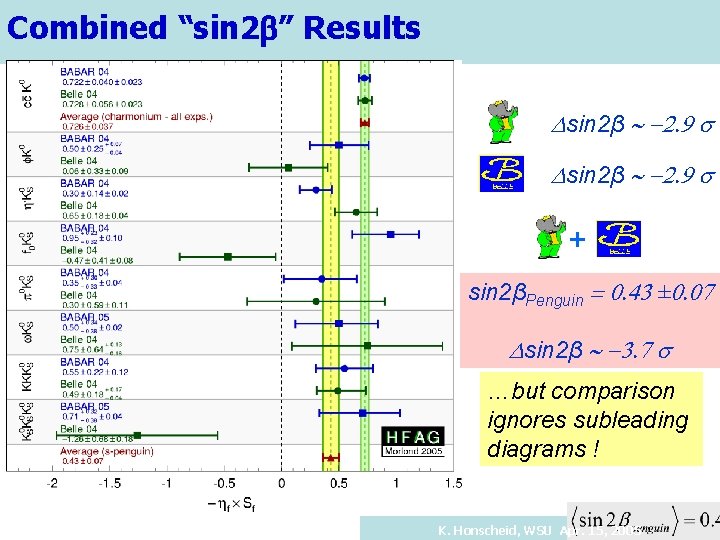
Combined “sin 2 b” Results Dsin 2β ~ -2. 9 s + sin 2βPenguin = 0. 43 ± 0. 07 Dsin 2β ~ -3. 7 s …but comparison ignores subleading diagrams ! K. Honscheid, WSU Apr. 15, 2005

Corrections: b→s Decay Amplitude ~ Vub. Vus* penguin u • Decays involving Vub enter with decay phase g • Doubly-CKM suppressed w. r. t dominant diagram color-suppressed tree Contribute to h’Ks, f 0 Ks, w. Ks, but not Ks [in KKKs (requires ss popup from soft g)] s s Contributes to all b sss modes color-allowed tree Contribute to non-resonant KKKs (requires ss popup from soft g) K. Honscheid, WSU Apr. 15, 2005

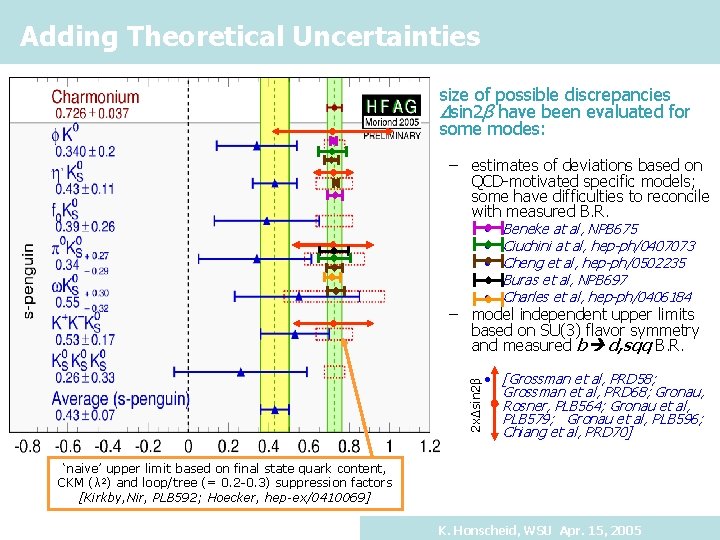
Adding Theoretical Uncertainties • size of possible discrepancies Δsin 2β have been evaluated for some modes: – estimates of deviations based on QCD-motivated specific models; some have difficulties to reconcile with measured B. R. • • • Beneke at al, NPB 675 Ciuchini at al, hep-ph/0407073 Cheng et al, hep-ph/0502235 Buras et al, NPB 697 Charles et al, hep-ph/0406184 2 xΔsin 2β – model independent upper limits based on SU(3) flavor symmetry and measured b d, sqq B. R. • [Grossman et al, PRD 58; Grossman et al, PRD 68; Gronau, Rosner, PLB 564; Gronau et al, PLB 579; Gronau et al, PLB 596; Chiang et al, PRD 70] ‘naive’ upper limit based on final state quark content, CKM (λ 2) and loop/tree (= 0. 2 -0. 3) suppression factors [Kirkby, Nir, PLB 592; Hoecker, hep-ex/0410069] K. Honscheid, WSU Apr. 15, 2005

Conclusion • Almost 40 years after the discovery of CP violation in the kaon system we are finally in a position to improve our understanding of CP violation in the Standard Model • Belle and Ba. Bar give consistent results for sin 2 b. Both work extremely well • The SM prediction of a single phase in the CKM matrix as cause of CP violation appears to be correct. • We now know how to distinguish between matter and anti-matter aliens. • New Physics will be needed to explain the baryon asymmetry in the universe • Will we find hints in CP phases and/or rare decays? • Stay tuned as more data is coming in. K. Honscheid, WSU Apr. 15, 2005