A Parallelisation Approach for MultiResolution Grids Based Upon

A Parallelisation Approach for Multi-Resolution Grids Based Upon the Peano Space-Filling Curve Student: Adriana Bocoi Advisor: Dipl. -Inf. Tobias Weinzierl

Content n Domain n Trees discretisation [Computer representation] n Space-Filling Curves [Traversal] n Parallelisation 01. 04. 2007 Adriana Bocoi - Peano space filling curve 2

Solving Real Life Problems n Model the real life problem n Usually we end up with PDE (Partial Differential Equations) n Consider the domain n Discretise (grid) n Solve the discrete problem 01. 04. 2007 Adriana Bocoi - Peano space filling curve 3

Parallelisation Parallel computing is the division of one task into a set of subtasks assigned to multiple processors in order to obtain results faster or to reduce memory requirements per processor. Example: input: a={2, 3, 4}, b={5, 6, 1} result: c=a+b={7, 9, 5} Serial 01. 04. 2007 Parallel (3 processors) Adriana Bocoi - Peano space filling curve 4

Domain Partitioning Domain partitioning is the process of dividing a domain into two or more regions. 01. 04. 2007 Adriana Bocoi - Peano space filling curve 5

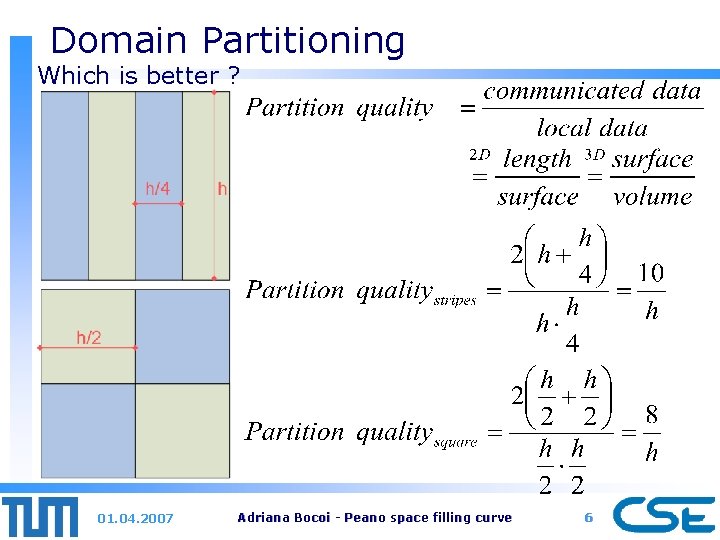
Domain Partitioning Which is better ? 01. 04. 2007 Adriana Bocoi - Peano space filling curve 6

Domain Partitioning We have (regarding partition quality): stripes < square Which is optimal ? Minimum length/maximum surface -> circle thus: stripes < square < circle 01. 04. 2007 Adriana Bocoi - Peano space filling curve 7

Domain Partitioning n Types of structured grids: ¨ Regular grids ¨ Adaptive 01. 04. 2007 grids Adriana Bocoi - Peano space filling curve 8

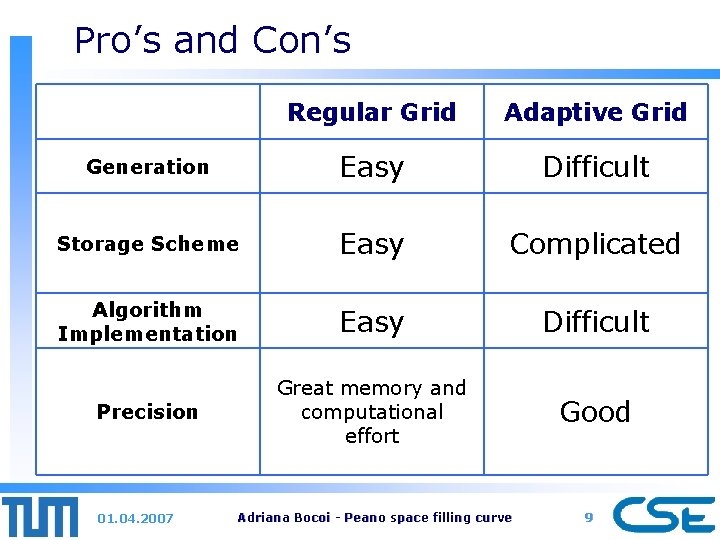
Pro’s and Con’s Regular Grid Adaptive Grid Generation Easy Difficult Storage Scheme Easy Complicated Algorithm Implementation Easy Difficult Precision Great memory and computational effort Good 01. 04. 2007 Adriana Bocoi - Peano space filling curve 9

Conclusion Grids If we can find a way to memorise and work with adaptive grids efficiently, they can help us to make more precise computations with less effort (memory and computation). 01. 04. 2007 Adriana Bocoi - Peano space filling curve 10

Content n Domain n Trees discretisation [Computer representation] n Space-Filling Curves [Traversal] n Parallelisation 01. 04. 2007 Adriana Bocoi - Peano space filling curve 11

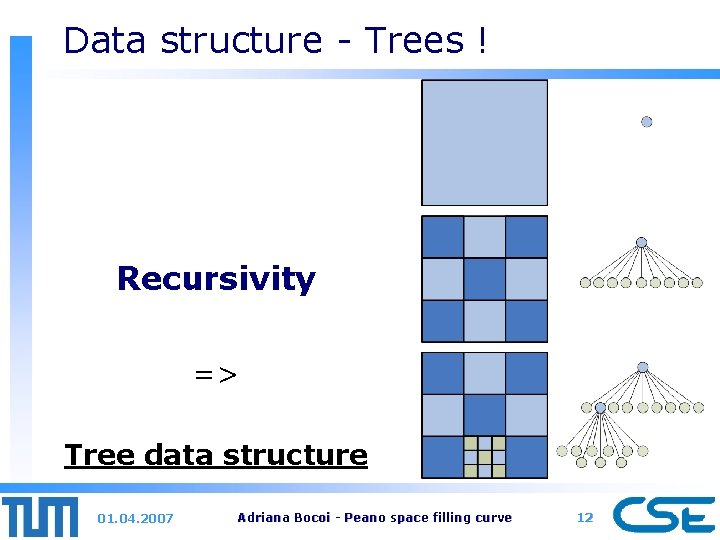
Data structure - Trees ! Recursivity => Tree data structure 01. 04. 2007 Adriana Bocoi - Peano space filling curve 12

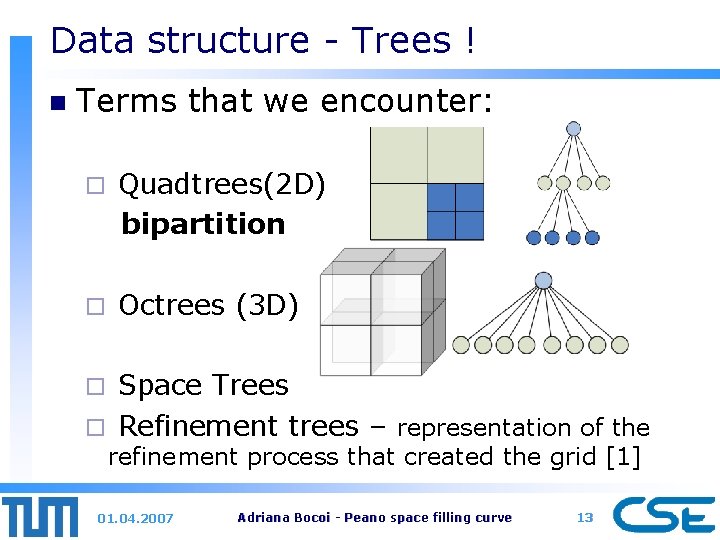
Data structure - Trees ! n Terms that we encounter: ¨ Quadtrees(2 D) bipartition ¨ Octrees (3 D) Space Trees ¨ Refinement trees – representation of the ¨ refinement process that created the grid [1] 01. 04. 2007 Adriana Bocoi - Peano space filling curve 13

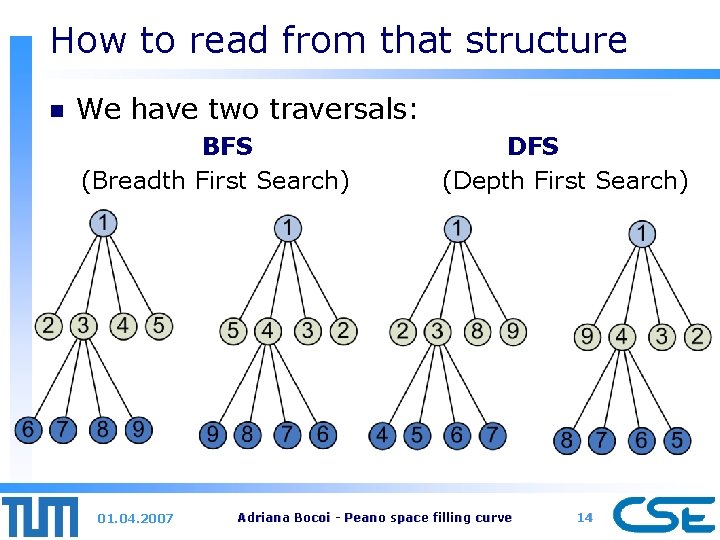
How to read from that structure n We have two traversals: BFS (Breadth First Search) 01. 04. 2007 DFS (Depth First Search) Adriana Bocoi - Peano space filling curve 14

Ordering Deterministic algorithm (Where to go next ? ) 01. 04. 2007 Adriana Bocoi - Peano space filling curve 15

Content n Domain n Trees discretisation [Computer representation] n Space-Filling Curves [Traversal] n Parallelisation 01. 04. 2007 Adriana Bocoi - Peano space filling curve 16

We need an unique ordering We have space filling curves to define the order of the children The Peano Space Filling Curve 01. 04. 2007 Adriana Bocoi - Peano space filling curve 17

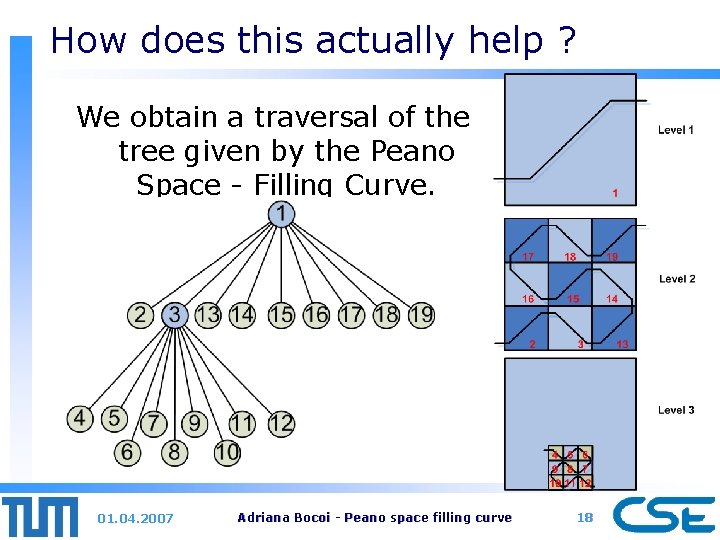
How does this actually help ? We obtain a traversal of the tree given by the Peano Space - Filling Curve. 01. 04. 2007 Adriana Bocoi - Peano space filling curve 18

What do we have till now ? Adaptive grids n Methods to handle them on the computer n ¨ Data Structure: Tree Structure ¨ Ordering: 01. 04. 2007 Peano Space-Filling Curve Adriana Bocoi - Peano space filling curve 19

Content n Domain n Trees discretisation [Computer representation] n Space-Filling Curves [Traversal] n Parallelisation 01. 04. 2007 Adriana Bocoi - Peano space filling curve 20

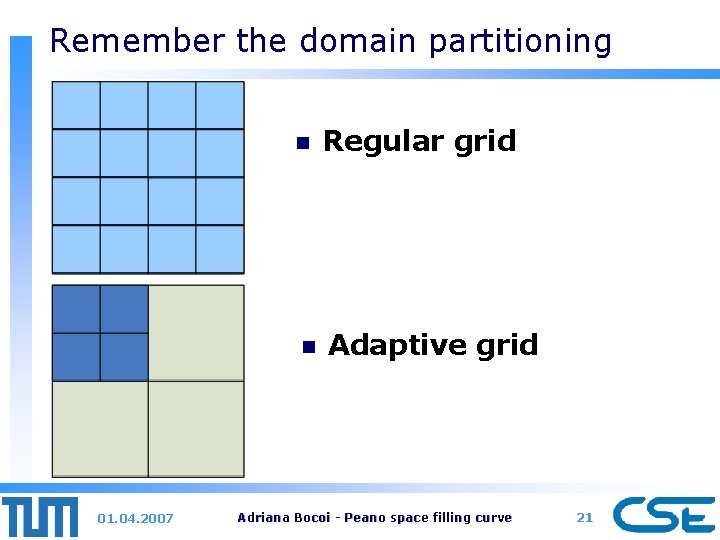
Remember the domain partitioning 01. 04. 2007 n Regular grid n Adaptive grid Adriana Bocoi - Peano space filling curve 21

Parallelisation What is wrong? 01. 04. 2007 n Regular grids – nothing n Adaptive grids - One processor has to do more work than the other three! [Load imbalance] Adriana Bocoi - Peano space filling curve 22

We want a well-balanced workload distribution! Load balancing is a technique to spread work between processors in order to get better resource utilisation and, thus, decrease computing time. 01. 04. 2007 Adriana Bocoi - Peano space filling curve 23

Partition strategy split the grid <=> split the tree n One strategy [1]: n ¨p processors ¨ n nodes in the tree ¨ we get approx. [n/p] nodes for each processor 01. 04. 2007 Adriana Bocoi - Peano space filling curve 24

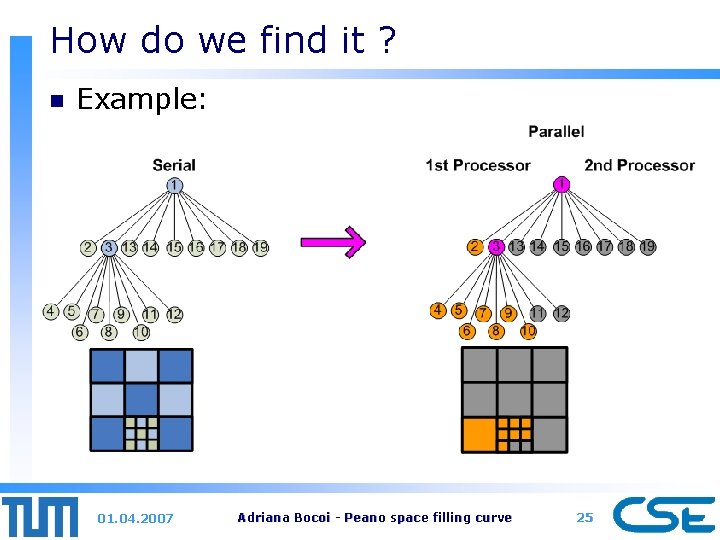
How do we find it ? n Example: 01. 04. 2007 Adriana Bocoi - Peano space filling curve 25

How good is the partition ? The papers in this field [2] tell us that actually domain partitioning using Peano Space-Filling Curves is besides a constant as good as an optimal partitioning (circle). n rectangle < square < peano SFC < circle 01. 04. 2007 Adriana Bocoi - Peano space filling curve 26

Why Peano and not other SFC ? Because of the 3 D projection propriety: 01. 04. 2007 Adriana Bocoi - Peano space filling curve 27

Conclusion Partitioned Domain + Trees as data structure + Peano space filling curve for ordering + Splitting strategy = Good parallelisation 01. 04. 2007 Adriana Bocoi - Peano space filling curve 28

Thank you for your attention !!! Q&A