A parabola is formed by the intersection of

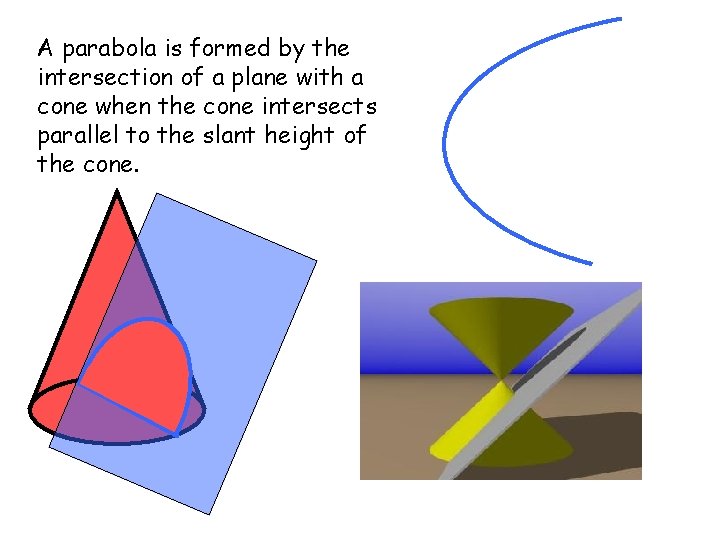
A parabola is formed by the intersection of a plane with a cone when the cone intersects parallel to the slant height of the cone.

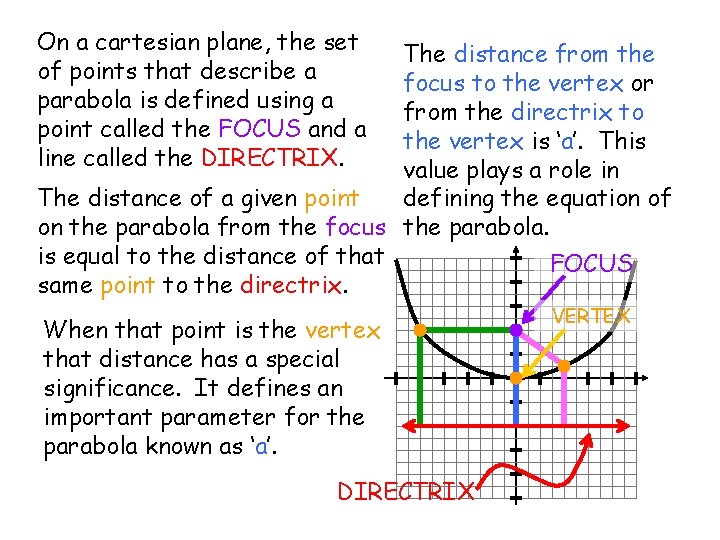
On a cartesian plane, the set of points that describe a parabola is defined using a point called the FOCUS and a line called the DIRECTRIX. The distance from the focus to the vertex or from the directrix to the vertex is ‘a’. This value plays a role in defining the equation of The distance of a given point on the parabola from the focus the parabola. is equal to the distance of that FOCUS same point to the directrix. When that point is the vertex that distance has a special significance. It defines an important parameter for the parabola known as ‘a’. DIRECTRIX VERTEX

Definition of Parabola A parabola is the locus of a variable point on a plane so that its distance from a fixed point (the focus) is equal to its distance from a fixed line (the directrix x = - a). N(-a, y) M(-a, 0) y P(x, y) O focus F(a, 0) x

From the definition of parabola, PF = PN standard equation of a parabola ‘a’ is positive

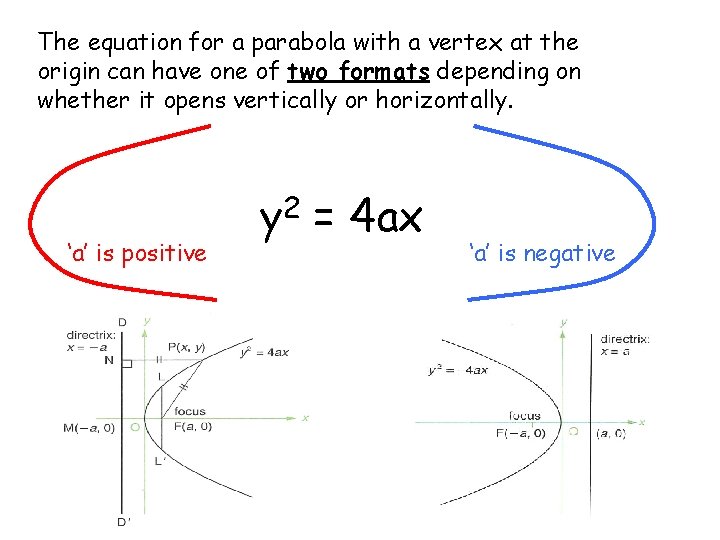
The equation for a parabola with a vertex at the origin can have one of two formats depending on whether it opens vertically or horizontally. ‘a’ is positive y 2 = 4 ax ‘a’ is negative

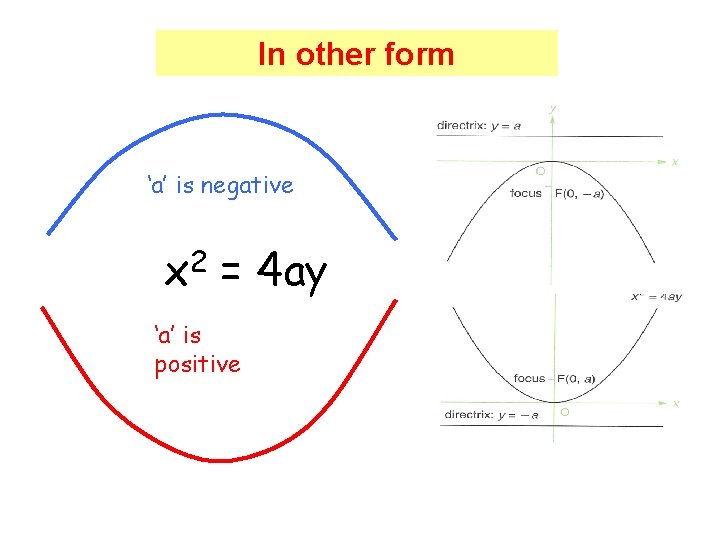
In other form ‘a’ is negative x 2 = 4 ay ‘a’ is positive

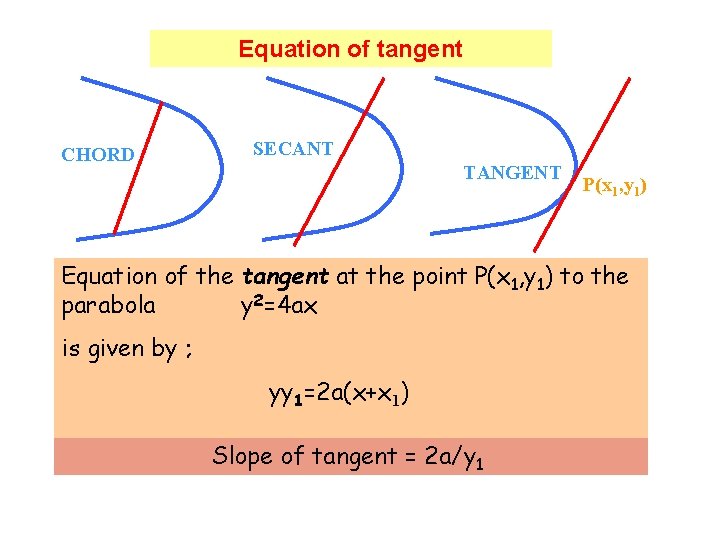
Equation of tangent CHORD SECANT TANGENT P(x 1, y 1) Equation of the tangent at the point P(x 1, y 1) to the parabola y 2=4 ax is given by ; yy 1=2 a(x+x 1) Slope of tangent = 2 a/y 1

Equation of normal NORMAL P(x 1, y 1) Equation of the normal at the point P(x 1, y 1) to the parabola y 2=4 ax is given by ; y - y 1 = y 1 / 2 a ( x - x 1 ) Slope of normal = -y 1/ 2 a

Equation of tangent and normal in parametric form Equation of the tangent to y 2 = 4 ax at the point (at 2, 2 at) is given by: yt = x+at 2 Equation of the normal to y 2 = 4 ax at the point (at 2, 2 at) is given by: y = –tx + 2 at + at 3.

Equation of normal in slope form Equation of the normal to y 2 = 4 ax in slope form is given by: y = mx - 2 am - am 3, where m is the parameter and (am 2, -2 am) is the point of contact. This cubic in m has three roots say; m 1, m 2, m 3, which shows that three normals can be drawn from any point to a parabola of which at least one must be real for imaginary roots of an equation with real coefficients occur in conjugate pairs. Also, m 1+ m 2+ m 3 = 0 i. e. the sum of the ordinates of the feet of the normals from a given point is zero.

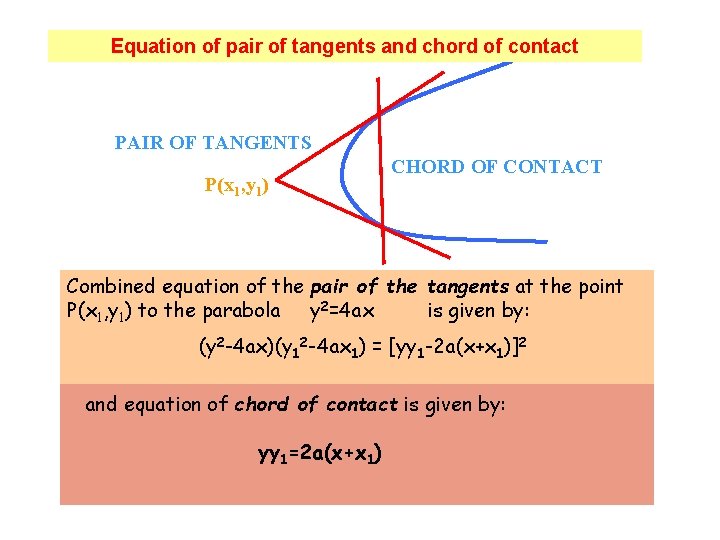
Equation of pair of tangents and chord of contact PAIR OF TANGENTS P(x 1, y 1) CHORD OF CONTACT Combined equation of the pair of the tangents at the point P(x 1, y 1) to the parabola y 2=4 ax is given by: (y 2 -4 ax)(y 12 -4 ax 1) = [yy 1 -2 a(x+x 1)]2 and equation of chord of contact is given by: yy 1=2 a(x+x 1)

Equation of chord in terms of its mid point. P(x 1, y 1) Equation of the chord of the parabola y 2=4 ax whose mid point is P(x 1, y 1) is given by ; yy 1 -( x + x 1 ) = y 12 – 4 ax 1

Parabolas show up in the architecture of bridges, in fountains etc