A Numerical Analysis Approach to Convex Optimization Richard















![[BCLL, STOC `18] [NN’ 94] a [BCLL ’ 18] p [BCLL, STOC `18] [NN’ 94] a [BCLL ’ 18] p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-22.jpg)
![[AKPS, SODA `19] [NN’ 94] a [BCLL ’ 18] [AKPS `19] p [AKPS, SODA `19] [NN’ 94] a [BCLL ’ 18] [AKPS `19] p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-23.jpg)
![[AKPS, SODA `19] [NN’ 94] a [BCLL ’ 18] [AKPS `19] p [AKPS, SODA `19] [NN’ 94] a [BCLL ’ 18] [AKPS `19] p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-24.jpg)
![On graphs, using more graphs m 1. 5 [LS `19]: m 11/8+o(1) via p On graphs, using more graphs m 1. 5 [LS `19]: m 11/8+o(1) via p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-25.jpg)















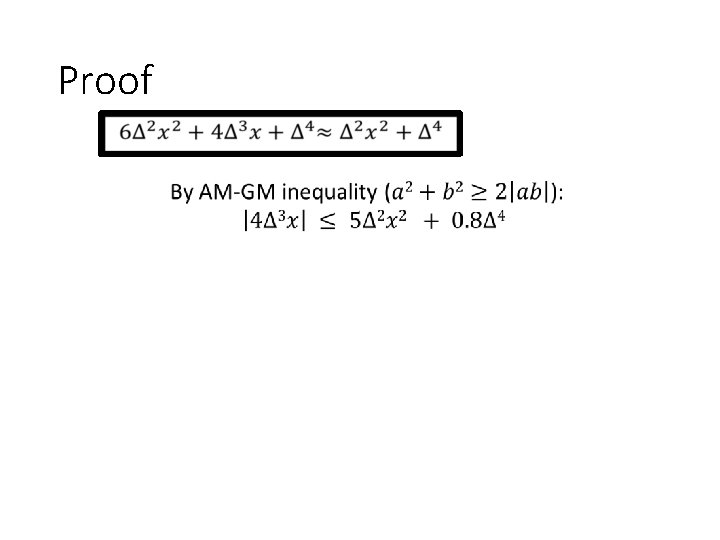


![[APS Neurips `19]: Provable IRLS [APS Neurips `19]: Provable IRLS](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-50.jpg)
![[APS Neurips `19] IRLS vs. CVX [APS Neurips `19] IRLS vs. CVX](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-51.jpg)
![Summary [NN’ 94] a [BCLL ’ 18] [AKPS `19] p Summary [NN’ 94] a [BCLL ’ 18] [AKPS `19] p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-52.jpg)
- Slides: 52

A Numerical Analysis Approach to Convex Optimization Richard Peng

Optimization

Convex Optimization

Convex Optimization Poly-time convex optimization led to: • Approximation algorithms • Sparse recovery • Support vector machines

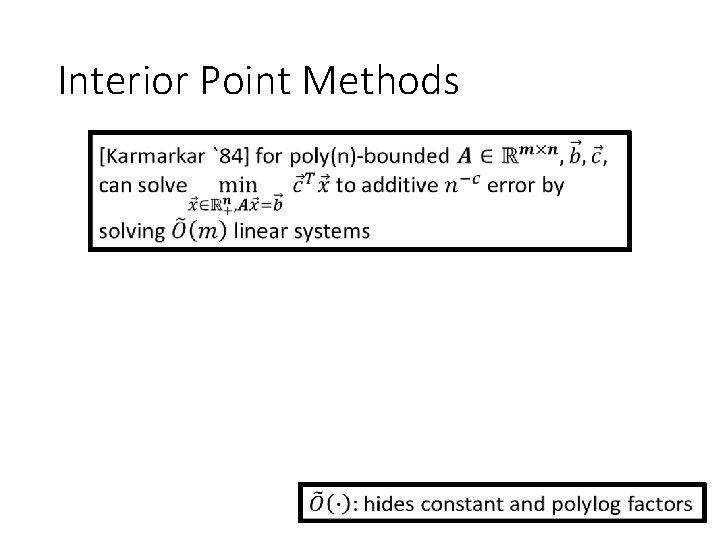
Interior Point Methods

Interior Point Methods

Interior Point Methods

Lighter Weight Tools: • • • (Stochastic) (Accelerated) (gradient / mirror / coordinate) descent Alternating direction method of multipliers (ADMM) Regret minimization / MWU

Why High Accuracy Solvers?

This Talk New high accuracy algorithms for large classes of convex objectives • Faster convergence, • Better overall runtime, • Simpler algorithms

Outline


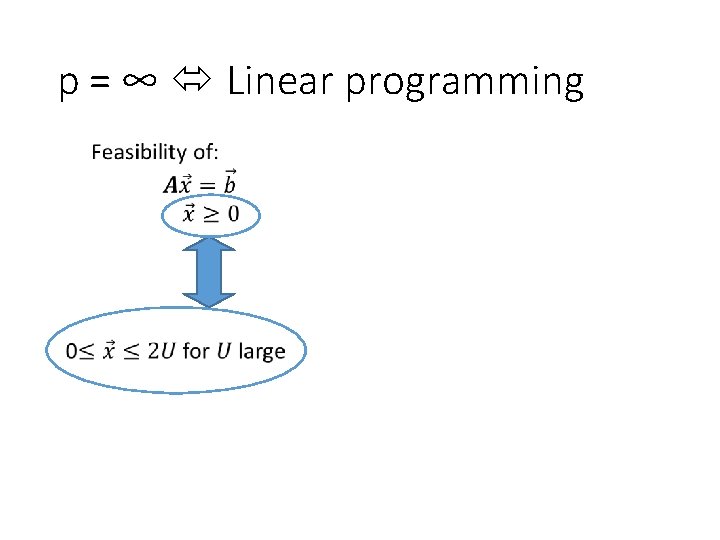
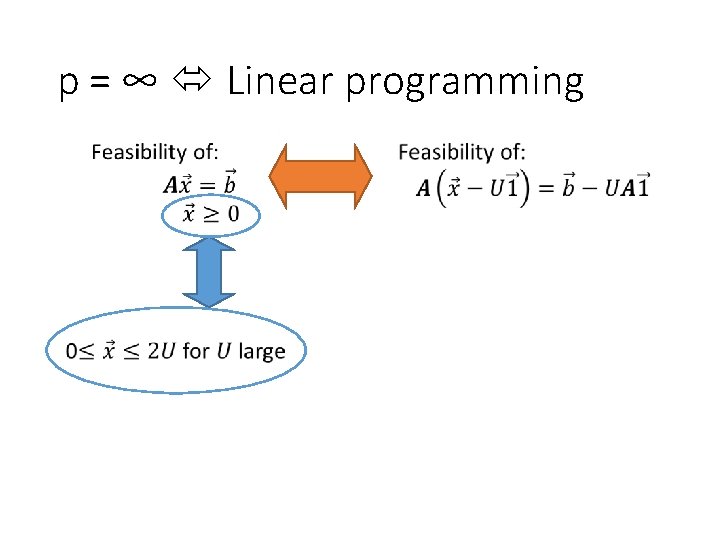
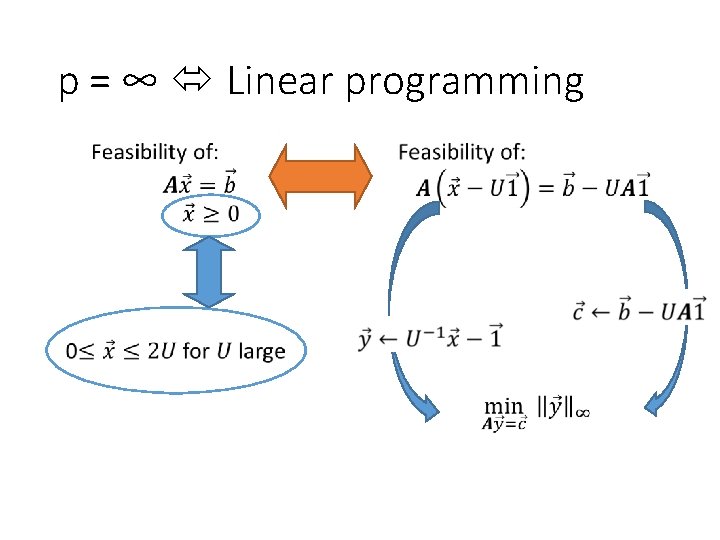
p = ∞ Linear programming

p = ∞ Linear programming

p = ∞ Linear programming

p = ∞ Linear programming

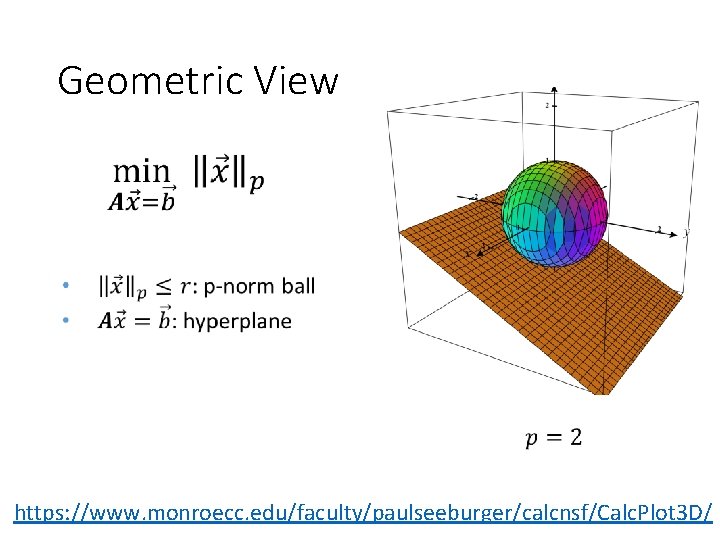
Geometric View https: //www. monroecc. edu/faculty/paulseeburger/calcnsf/Calc. Plot 3 D/

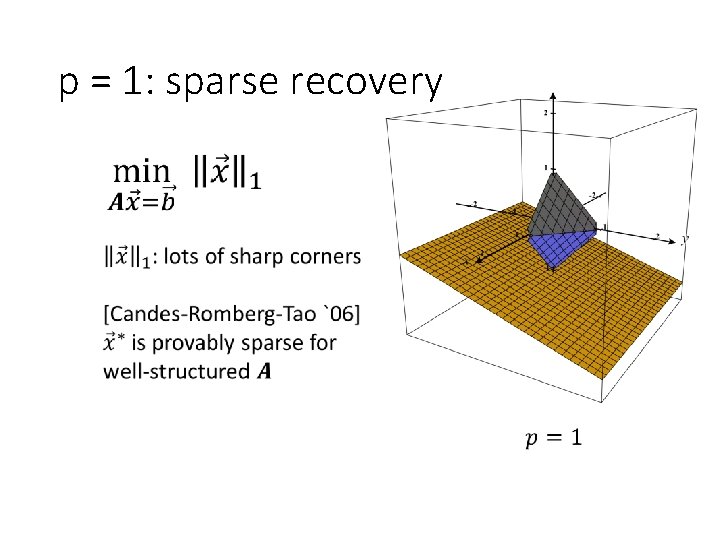
p = 1: sparse recovery

Other values of p Widely used due to availability of gradients (for back-propagation): • [El. Alaoui-Cheng-Ramdas. Wainwright-Jordan COLT 16]: p-norm regularization • [Ibrahami-Gleich WWW `19]: 1. 5&3 -norm diffusion for semi-supervised learning

On graphs p 1 2 ∞ Shortest Path Electrical flow Max-flow Min-cut Spring-mass system Negative cycle detection edge-vertex incidence matrix Beu = -1/1 for endpoints u 0 everywhere else

Norms & Algorithms • Gaussian distributions arise naturally, but were the method of choice for modeling because [Gauss 1809] came with efficient algorithms • Laplace distributions now much more common in machine learning, signal processing, privacy…
![BCLL STOC 18 NN 94 a BCLL 18 p [BCLL, STOC `18] [NN’ 94] a [BCLL ’ 18] p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-22.jpg)
[BCLL, STOC `18] [NN’ 94] a [BCLL ’ 18] p
![AKPS SODA 19 NN 94 a BCLL 18 AKPS 19 p [AKPS, SODA `19] [NN’ 94] a [BCLL ’ 18] [AKPS `19] p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-23.jpg)
[AKPS, SODA `19] [NN’ 94] a [BCLL ’ 18] [AKPS `19] p
![AKPS SODA 19 NN 94 a BCLL 18 AKPS 19 p [AKPS, SODA `19] [NN’ 94] a [BCLL ’ 18] [AKPS `19] p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-24.jpg)
[AKPS, SODA `19] [NN’ 94] a [BCLL ’ 18] [AKPS `19] p
![On graphs using more graphs m 1 5 LS 19 m 118o1 via p On graphs, using more graphs m 1. 5 [LS `19]: m 11/8+o(1) via p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-25.jpg)
On graphs, using more graphs m 1. 5 [LS `19]: m 11/8+o(1) via p = O(log 1/2 n) in inner loop runtime m 1. 33 m 1 2 value of p 4 ∞

Outline

Quadratic minimization solving a system of linear equations • Gaussian elimination / exact method • Iterative / numerical methods

Quadratic minimization solving a system of linear equations • Gaussian elimination / exact method • Iterative / numerical methods Build upon these, since we’re looking for iterative convergence



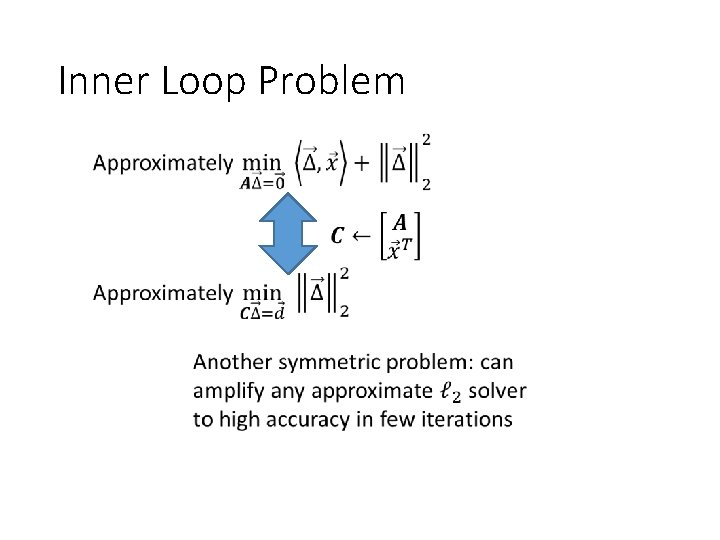
Inner Loop Problem

Ideal Algorithm: %s/2/p Replace all 2 s by ps: Solve p-norm regression to high accuracy by solving a sequence of p-norm regression problems, each to low accuracy •

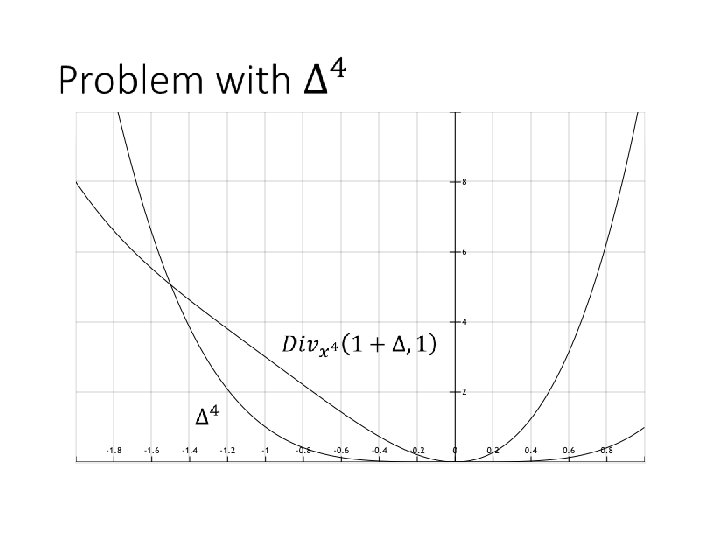
Replace 2 s by 4 s?

Replace 2 s by 4 s?

Outline

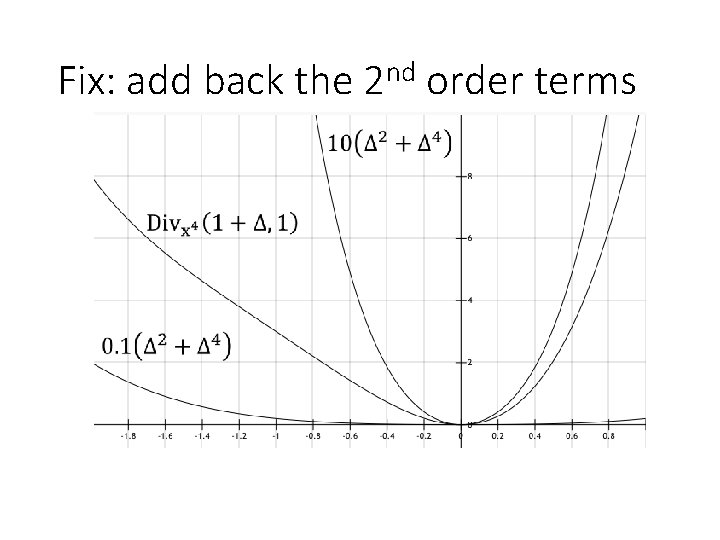
Replace 2 s by ps, but keep the 2 s

Replace 2 s by ps, but keep the 2 s Key difference: add back the quadratic term

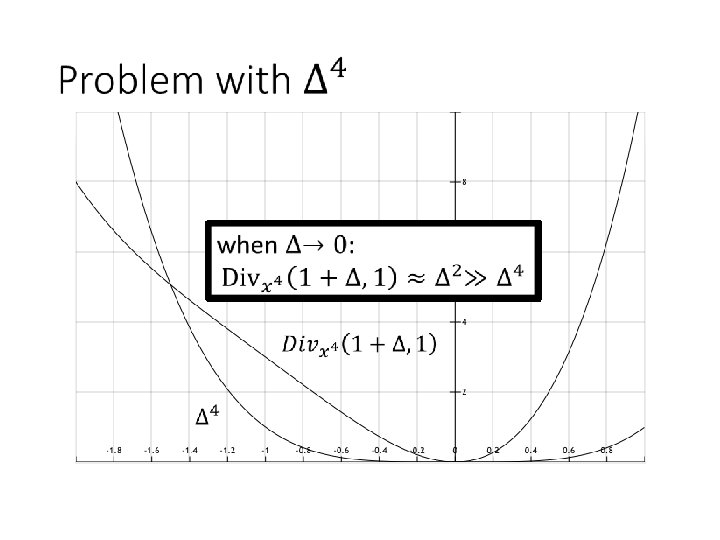
Issue replacing 2 s by 4 s? ≈ Can study this issue entry-wise

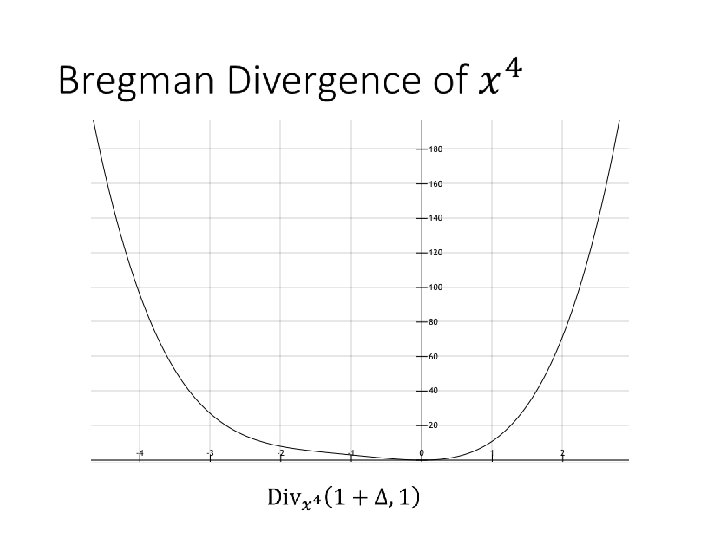
Sufficient Condition Bregman Divergence: contribution of higher (2 nd after) order terms = Integral over 2 nd order derivative Sufficient and necessary: problem in inner loop approximates the Bregman Divergence




Fix: add back the 2 nd order terms

Fixed algorithm

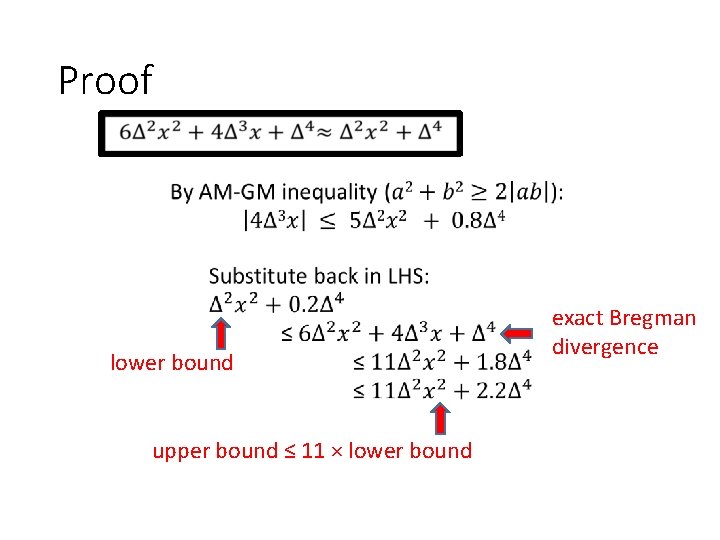
Proof
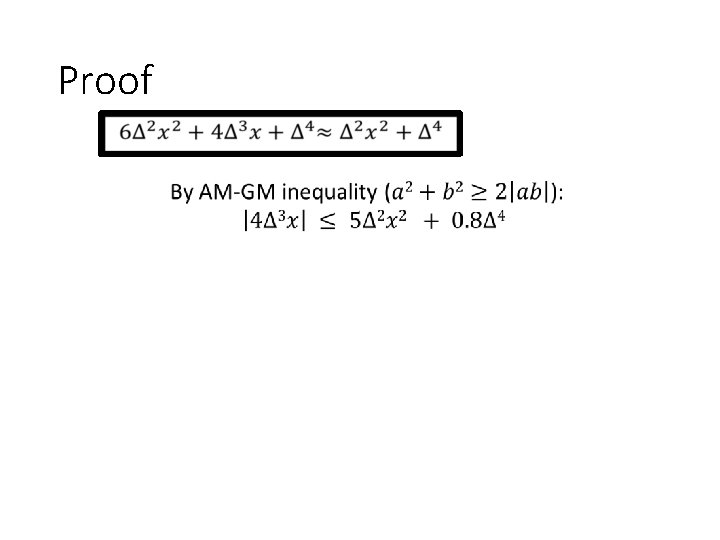
Proof

Proof lower bound upper bound ≤ 11 × lower bound exact Bregman divergence

Outline

Iterative Reweighted Least Squares
![APS Neurips 19 Provable IRLS [APS Neurips `19]: Provable IRLS](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-50.jpg)
[APS Neurips `19]: Provable IRLS
![APS Neurips 19 IRLS vs CVX [APS Neurips `19] IRLS vs. CVX](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-51.jpg)
[APS Neurips `19] IRLS vs. CVX
![Summary NN 94 a BCLL 18 AKPS 19 p Summary [NN’ 94] a [BCLL ’ 18] [AKPS `19] p](https://slidetodoc.com/presentation_image_h2/9bfc3416c9eab3f0aba4f6f47e9c06a3/image-52.jpg)
Summary [NN’ 94] a [BCLL ’ 18] [AKPS `19] p