A Novel Algorithm and Architecture for High Speed

A Novel Algorithm and Architecture for High Speed Pattern Matching in Resourcelimited Silicon Solution Authors: Nen-Fu Huang, Yen-Ming Chu, Chi-Hung Tsai, Chen. Ying Hsieh and Yih-Jou Tzang Publisher: ICC 2007 Present: Chen-Yu Lin (林呈俞) Date: Oct, 8, 2007

Outline l l Introduction Magic State-based Heuristic (MSH) Algorithm An Example Evaluation

Introduction l NIDS/NIPS are designed to detect and identify worms, virus, and malicious code by performing deep packet inspecting on packet payloads. l Signature-based NIDS l • Snort • Over 2500 patterns as signatures. • Spend more than 80% CPU time on string matching NIDS needs fast string matching algorithm to reduce its load.

Introduction l Proposed string matching algorithms • • l Boyer Moore • Solve single-pattern matching problem Aho - Corasick and Wu - Manber • Solve multi-pattern matching Proposed hardware-based implementation • • AC-Bitmap Parallel bloom-filter Reconfigurable silicon hardware TCAM-based mechanism

Introduction l Budget problem • • l l Enterprise environments. • It is not the major concern. Medium-sized enterprise (SME) • It almost the key concern. Providing a high-speed but low-cost string matching with limited resource Consider the SME • • Limited cost and resources Most of the networks in SME are wire-speed of 100 Mbps. LAN WAN DMZ The processing speed must faster than 300 Mbps

Magic State-based Heuristic l General automaton-based string matching model State transition by state table Search the pattern ID

Magic State-based Heuristic (cont) 8 l l 16 Index = { x : y } • • X : input symbol Y : current state Snort 2. 4 patterns is 21584 v = 16

Magic State-based Heuristic (cont) l State table can be represented as state transition matrix symbol state l l u bit size of a symbol v bit size of a state a (x, y) = next state when the current state is y and the input symbol is x

Magic State-based Heuristic (cont) l Magic state • • • When A is a DFA, for each symbol x, most of a(x, y) have the same value for different current state y. Call these elements “magic state” ms(x) : the next state that appears most frequently with symbol x. l If we know that the next state is a magic state, then the state table lookup can be skipped. l Use another bitmap matrix (say B) to indicate whether an element in A is as magic state.

Magic State-based Heuristic (cont) l Bitmap matrix B

Magic State-based Heuristic (cont) l Matrices Construction • • • l Automaton Transition Matrix A Magic State Matrix M • Stores the corresponding magic state ms(x) in the element Heuristic Index Matrix H • Stores some information about whether a(x, y) equals to Reduce the size of bitmap matrix B (become matrix H) • Partition into • Each block size is blocks

Magic State-based Heuristic (cont) l Construct the Heuristic index matrix H • Matrix B Matrix H Perform AND operation to each block l Compression ratio (CR) • CR =

Magic State-based Heuristic (cont) l Heuristic Pattern Matching with Magic State Examining 0 It’s maybe a magic state Get the next state from matrix A in matrix H 1 It’s a magic state Get the magic state in matrix M directly

An Example l To illustrate the proposed algorithm 0 x 31 0 x 32 0 x 33 0 x 34 0 x 35 Correspond value • M = [178, 671, 2718, 2732, 4600] (Magic state matrix)

An Example l Suppose : m = n = 1

An Example l l Case 1: • State 35 receives input symbol 0 x 34 • Get the magic state 2732 if symbol 0 x 34 from matrix M 1 Case 2: • State 42 receives input symbol 0 x 31 0 • Access matrix A to get the next state 178 (Actually it is a magic state).

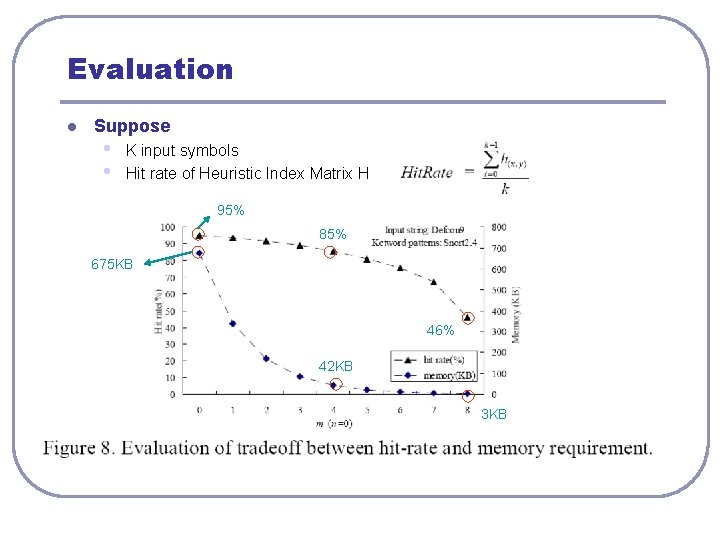
Evaluation l Suppose • • K input symbols Hit rate of Heuristic Index Matrix H 95% l 85% 675 KB 46% 42 KB 3 KB

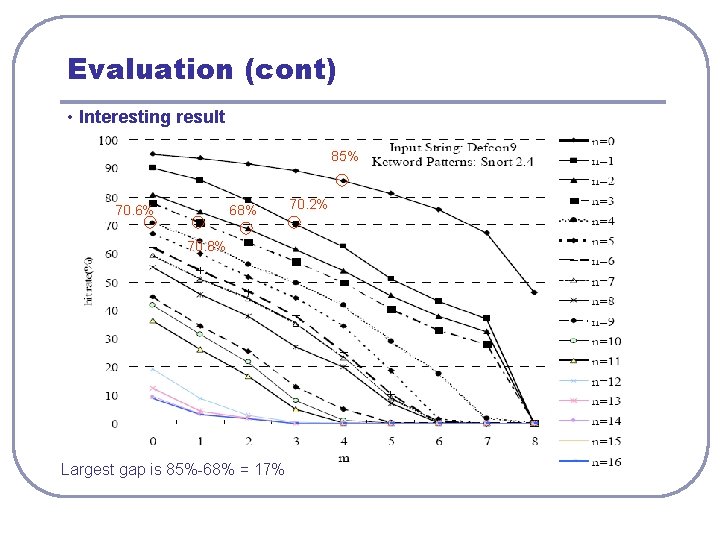
Evaluation (cont) l l Magic State • • • Snort 2. 4 has 21584 pattern. With 256 symbols Total 21584*256 = 5525504 element in matrix A. There are 5243748 magic states (94. 9%). Hit. Rate vs. Compression Ratio (CR) • • Value of m and n impact the Hit. Rate Higher CR conducts a lower hit rate.

Evaluation (cont) • Interesting result 85% 70. 6% 68% 70. 8% Largest gap is 85%-68% = 17% 70. 2%

Evaluation (cont) l False Negative • • When (m, n) = (4, 0) there are 15% state transition that we don’t sure the next state is a magic state. • Need to access Automaton Transition Matrix Among these 15%, only 5% are non-magic states. • Thus, 10% state transitions is false negative.

Evaluation (cont) l Total time of state transition • If matrix M and matrix H can be accessed concurrently • Algorithm without employing magic state • The proposed algorithm has a throughput gain

Evaluation (cont) l l l Memory space for matrices • • • Automaton Transition Table (ATT) Magic State Table (MST) Heuristic Index Table (HIT) MST & HIT are tiny, and can be stored into on-chip memory. ATT is too large, it can stored in DDR 2 SDRAM Simulation with (m, n) = (4, 0) Implementation model • • • Baseline Model MSH Model Multiple PMEs MSH Model

Evaluation (cont) l l Baseline Model • Throughput is 133. 33 Mbps MSH Model • Simulation throughput is 566 Mbps Store ATT

Evaluation (cont) Hit rate = 85%, throughput is 571. 42 Mbps. 4. 28 times faster than baseline model.

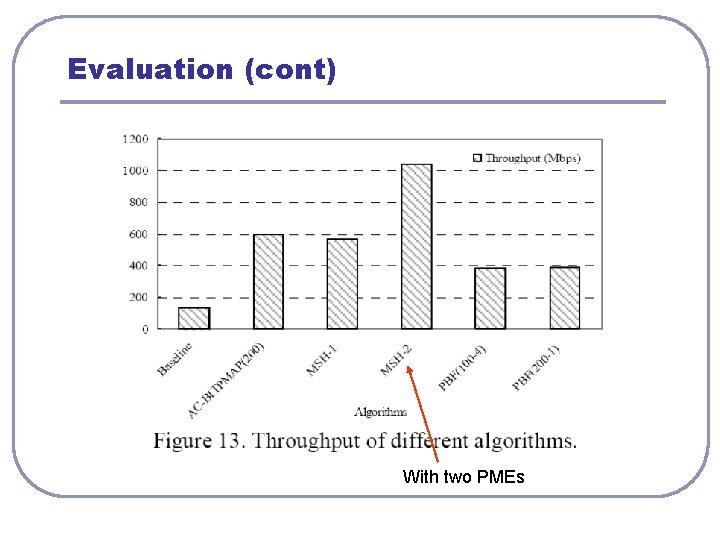
Evaluation (cont) l Multiple PMEs MSH Model • The proposed MSH can be further extended to have multiple PME in a single FPGA to process multiple sessions concurrently. Throughput is 1036. 26 Mbps, 7. 77 times faster than baseline model

Evaluation (cont) With two PMEs

Evaluation (cont) Cost of on-chip memory MSH-1 AC-Bitmap 42 KB 2 MB • FPGA-based solution is expensive • The solution can be implemented on off-chip high speed memory (SSRAM) • SSRAM faces the problem of very low throughput. • By utilizing the feature of Magic State more intelligently, the memory require of MSH reduce to less than 2 MB It can be stored into on-chip memory