A NMR pulse is often designed to detect

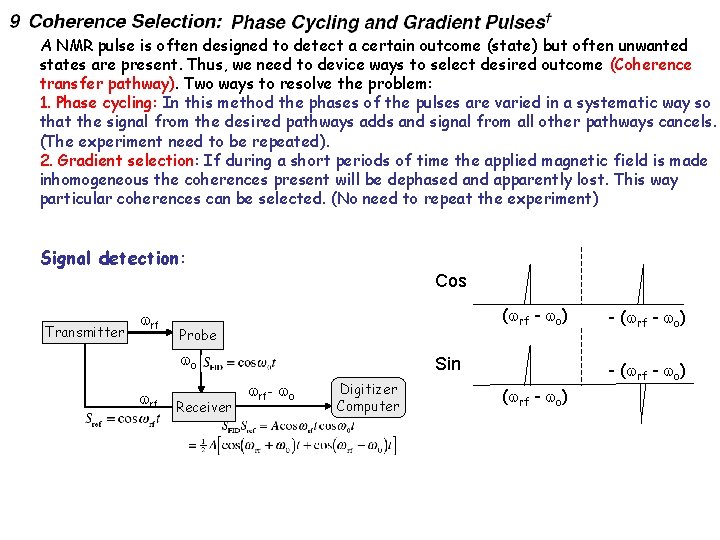
A NMR pulse is often designed to detect a certain outcome (state) but often unwanted states are present. Thus, we need to device ways to select desired outcome (Coherence transfer pathway). Two ways to resolve the problem: 1. Phase cycling: In this method the phases of the pulses are varied in a systematic way so that the signal from the desired pathways adds and signal from all other pathways cancels. (The experiment need to be repeated). 2. Gradient selection: If during a short periods of time the applied magnetic field is made inhomogeneous the coherences present will be dephased and apparently lost. This way particular coherences can be selected. (No need to repeat the experiment) Signal detection: Cos Transmitter rf ( rf - o) Probe o rf Receiver Sin rf - o Digitizer Computer - ( rf - o)

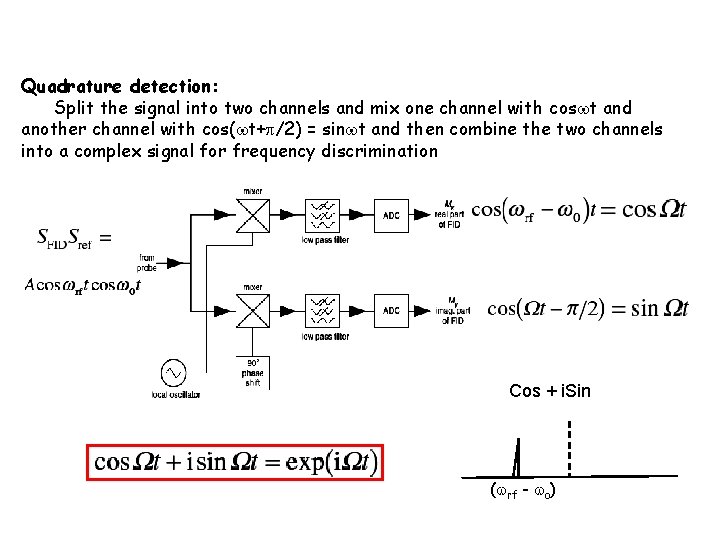
Quadrature detection: Split the signal into two channels and mix one channel with cos t and another channel with cos( t+ /2) = sin t and then combine the two channels into a complex signal for frequency discrimination Cos + i. Sin ( rf - o)

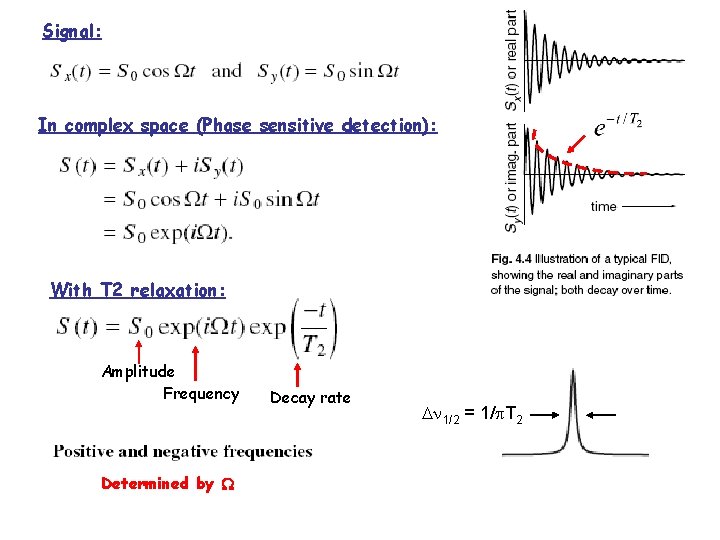
Signal: In complex space (Phase sensitive detection): With T 2 relaxation: Amplitude Frequency Determined by Decay rate 1/2 = 1/ T 2

Lineshape and Frequency Discrimination NMR signal: Lorentzian = Absorption (A) Dispersion (D)

: If the pulse is applied in X-direction, instead of Y-direction the dispersive and absorption signals will interchange their channels.

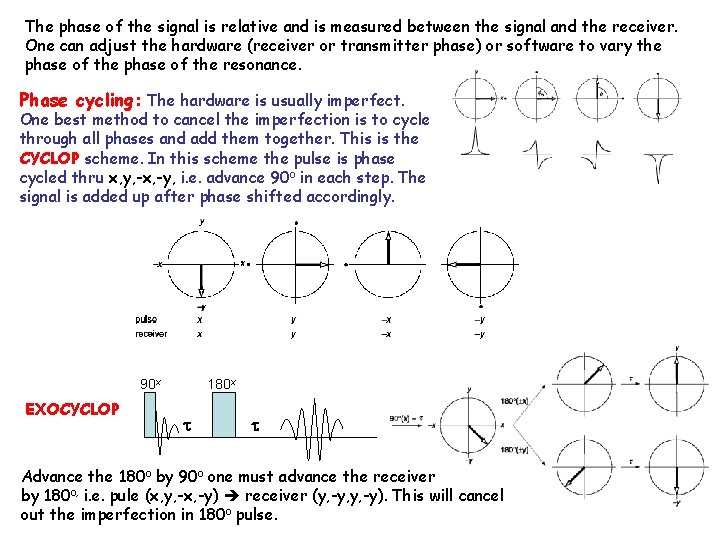
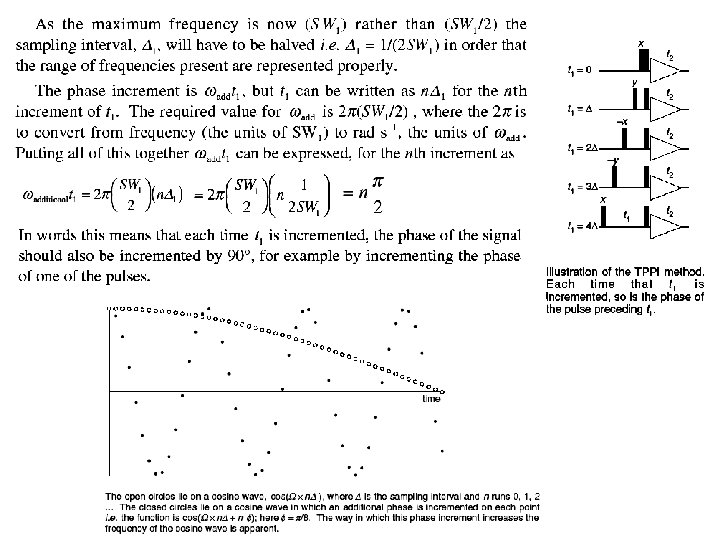
The phase of the signal is relative and is measured between the signal and the receiver. One can adjust the hardware (receiver or transmitter phase) or software to vary the phase of the resonance. Phase cycling: The hardware is usually imperfect. One best method to cancel the imperfection is to cycle through all phases and add them together. This is the CYCLOP scheme. In this scheme the pulse is phase cycled thru x, y, -x, -y, i. e. advance 90 o in each step. The signal is added up after phase shifted accordingly. 90 x EXOCYCLOP 180 x Advance the 180 o by 90 o one must advance the receiver by 180 o, i. e. pule (x, y, -x, -y) receiver (y, -y, y, -y). This will cancel out the imperfection in 180 o pulse.

(b spectrum) If only the sine component is recorded, i. e. then: (c spectrum) Both spectra b and c are said to lack frequency discrimination, differ from a. O needs both sine and cosine components to have frequency discrimination

Phase modulation: Amplitude modulation No frequency discrimination Phase alteration of the pulses to generate since and cosine modulation and combine them into a phase sensitive mode (Phase sensitive detection). Phase Modulation: In general, the 2 D spectrum will have the following form:

Two phase-twisted lines: (+ 1, + 2) (- 1, + 2) If we discard the imaginary part after the first Fourier transform we got: (No dispersive mode D)

modulated signal Two phase-twisted lines: : Similar results will be obtained if we start with the sine (+ 1, + 2) (- 1, + 2) But opposite signs If we discard the imaginary part after 1 st FT we can again obtain pure absorptive signal Combine the pure absorption mode cosine and sine modulated signal we got: One absorption line at (+ 1, + 2) In practice: The real part contains only one absorptive resonance at ( 1, 2)