A New Spherical Pulse Compressor Working with Degenerated

A New Spherical Pulse Compressor Working with Degenerated “Whispering Gallery” Mode Zongbin Li (SINAP), Alexej Grudiev (CERN), Wencheng Fang (SINAP), Qiang Gu (SINAP), Zhentang Zhao (SINAP) 07 -June-2018, HG 2018, Shanghai, China

Outline Ø Requirement Ø BOC Ø Analysis and RF design • TM 24, 1, 1 mode • TM 14, 1, 11 mode • TM 9, 1, 16 mode Ø Summary

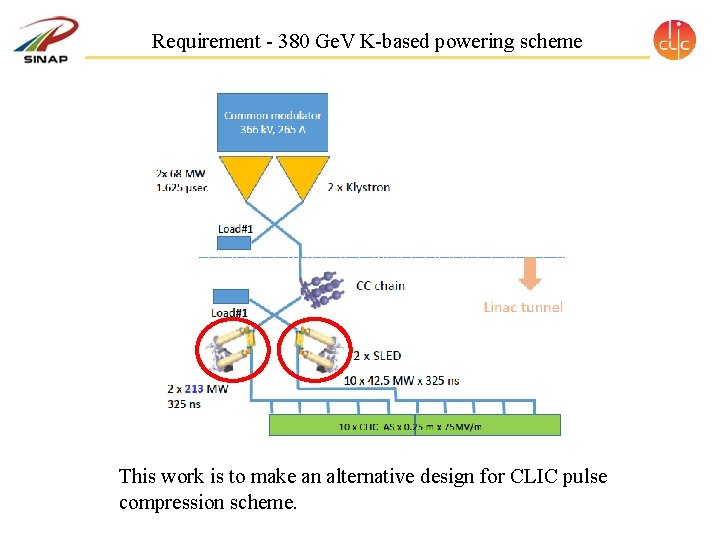
Requirement - 380 Ge. V K-based powering scheme This work is to make an alternative design for CLIC pulse compression scheme.

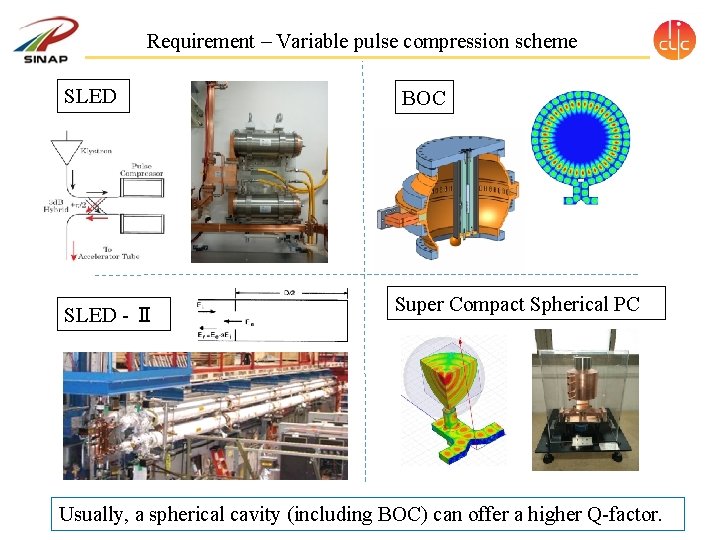
Requirement – Variable pulse compression scheme SLED - Ⅱ BOC Super Compact Spherical PC Usually, a spherical cavity (including BOC) can offer a higher Q-factor.

Outline Ø Requirement Ø BOC Ø Analysis and RF design • TM 24, 1, 1 mode • TM 14, 1, 11 mode • TM 9, 1, 16 mode Ø Summary

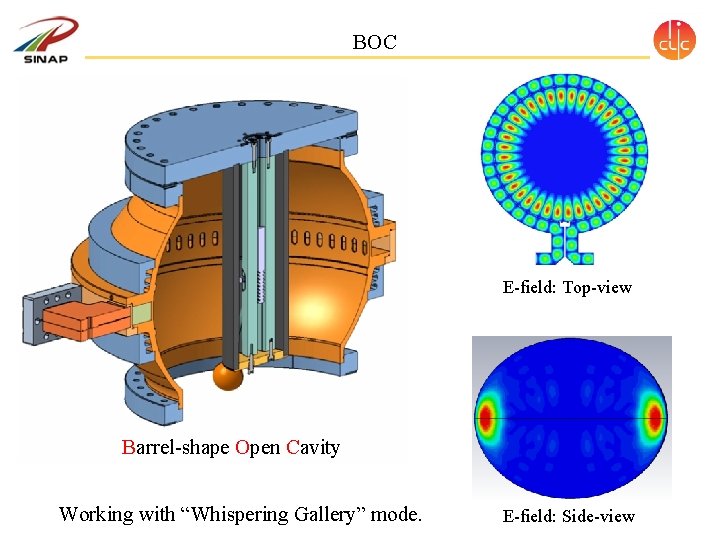
BOC E-field: Top-view Barrel-shape Open Cavity Working with “Whispering Gallery” mode. E-field: Side-view

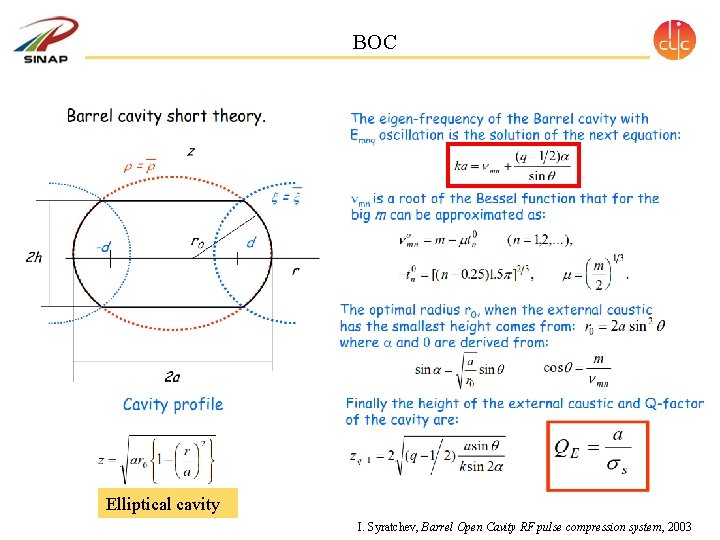
BOC Elliptical cavity I. Syratchev, Barrel Open Cavity RF pulse compression system, 2003

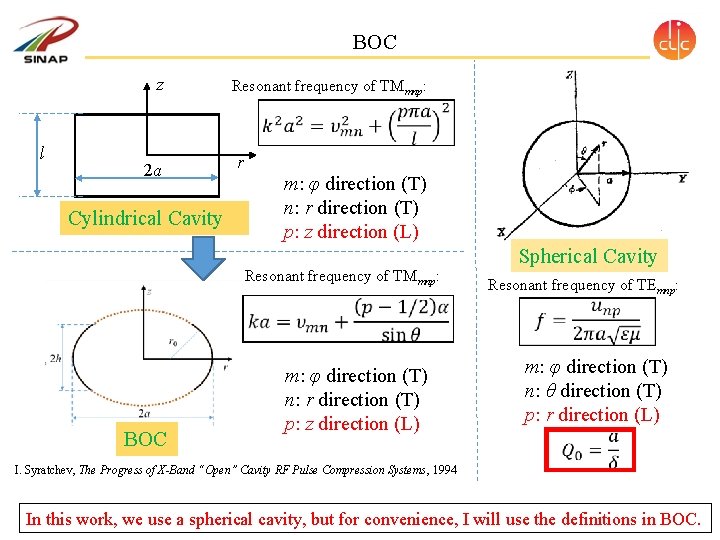
BOC z Resonant frequency of TMmnp: l 2 a r m: φ direction (T) n: r direction (T) p: z direction (L) Cylindrical Cavity Resonant frequency of TMmnp: BOC Spherical Cavity Resonant frequency of TEmnp: m: φ direction (T) n: r direction (T) p: z direction (L) m: φ direction (T) n: θ direction (T) p: r direction (L) I. Syratchev, The Progress of X-Band “Open” Cavity RF Pulse Compression Systems, 1994 In this work, we use a spherical cavity, but for convenience, I will use the definitions in BOC.

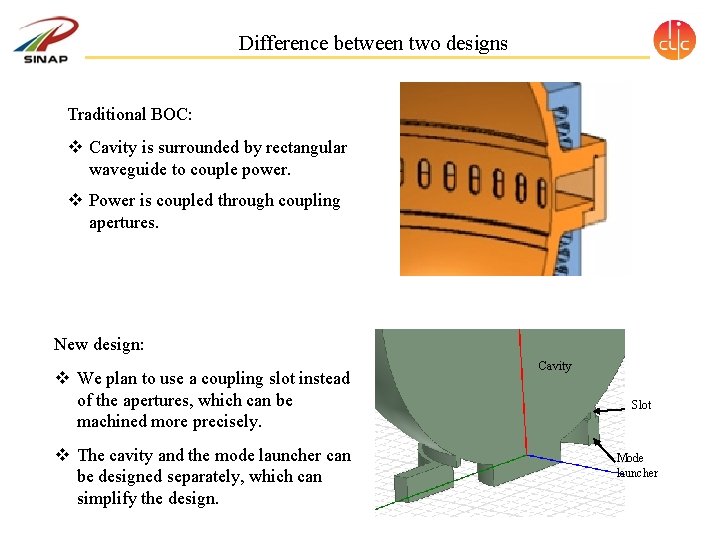
Difference between two designs Traditional BOC: v Cavity is surrounded by rectangular waveguide to couple power. v Power is coupled through coupling apertures. New design: v We plan to use a coupling slot instead of the apertures, which can be machined more precisely. v The cavity and the mode launcher can be designed separately, which can simplify the design. Cavity Slot Mode launcher

Outline Ø Requirement Ø BOC Ø Analysis and RF design • TM 24, 1, 1 (Whispering Gallery) mode • TM 14, 1, 11 mode • TM 9, 1, 16 mode Ø Summary

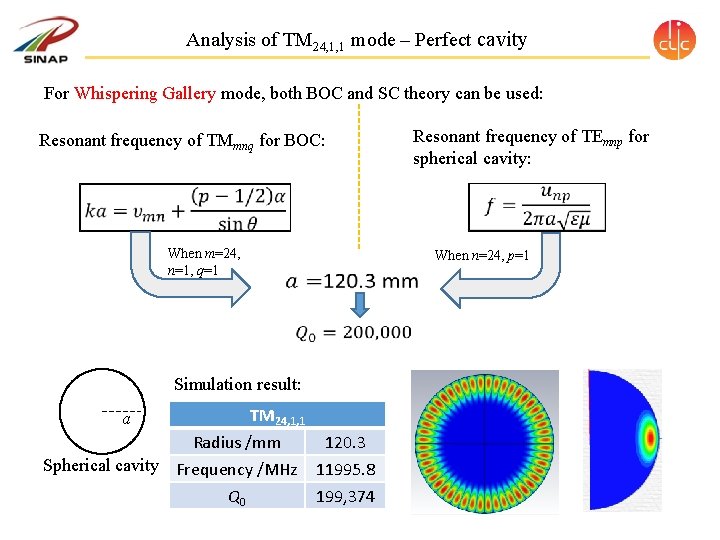
Analysis of TM 24, 1, 1 mode – Perfect cavity For Whispering Gallery mode, both BOC and SC theory can be used: Resonant frequency of TMmnq for BOC: Resonant frequency of TEmnp for spherical cavity: When m=24, n=1, q=1 When n=24, p=1 Simulation result: TM 24, 1, 1 Radius /mm 120. 3 Spherical cavity Frequency /MHz 11995. 8 Q 0 199, 374 a

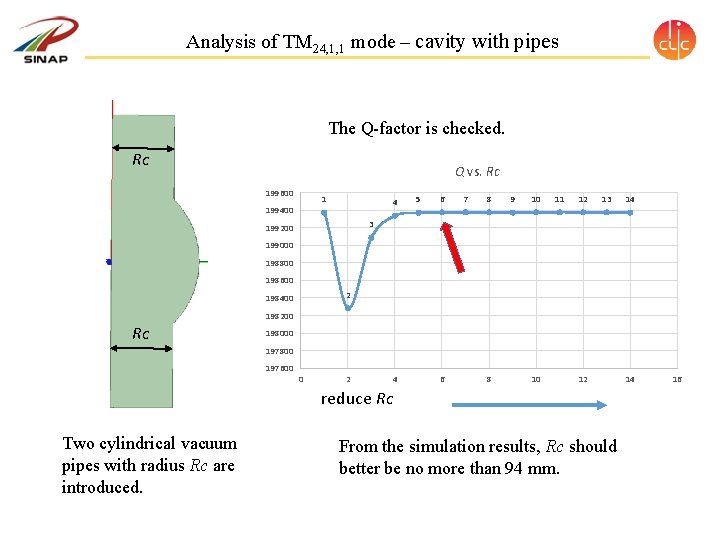
Analysis of TM 24, 1, 1 mode – cavity with pipes The Q-factor is checked. Rc Q vs. Rc 199600 1 4 199400 5 6 7 8 9 10 11 12 13 14 3 199200 199000 198800 198600 2 198400 198200 Rc 198000 197800 197600 0 2 4 6 8 10 12 reduce Rc Two cylindrical vacuum pipes with radius Rc are introduced. From the simulation results, Rc should better be no more than 94 mm. 14 16

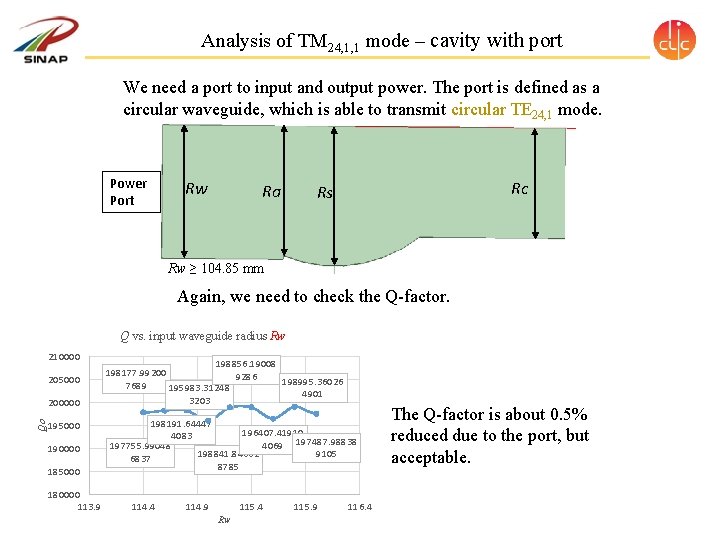
Analysis of TM 24, 1, 1 mode – cavity with port We need a port to input and output power. The port is defined as a circular waveguide, which is able to transmit circular TE 24, 1 mode. Power Port Rw Ra Rc Rs Rw ≥ 104. 85 mm Again, we need to check the Q-factor. Q vs. input waveguide radius Rw 210000 205000 Qo 200000 195000 190000 185000 180000 113. 9 198856. 19008 198177. 99200 9286 198995. 36026 7689 195983. 31248 4901 3203 198191. 64447 196407. 41910 4083 4069 197487. 98838 197755. 99048 198841. 84662 9105 6837 8785 114. 4 114. 9 115. 4 Rw 115. 9 116. 4 The Q-factor is about 0. 5% reduced due to the port, but acceptable.

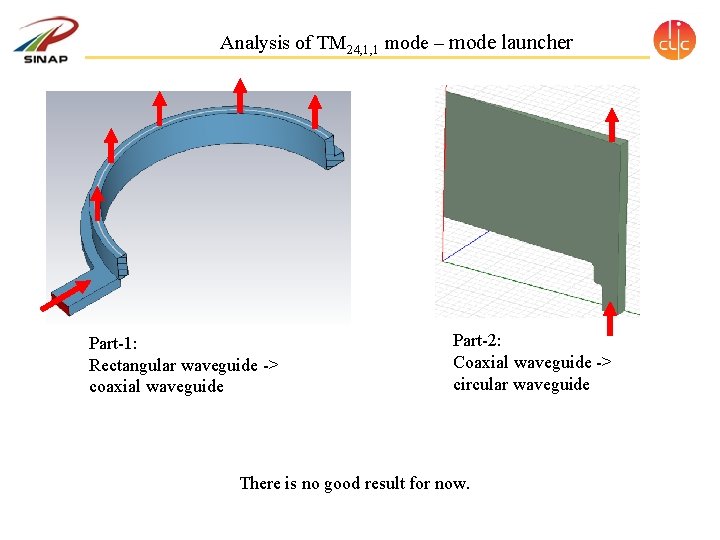
Analysis of TM 24, 1, 1 mode – mode launcher Part-1: Rectangular waveguide -> coaxial waveguide Part-2: Coaxial waveguide -> circular waveguide There is no good result for now.

Outline Ø Requirement Ø BOC Ø Analysis and RF design • TM 24, 1, 1 mode • TM 14, 1, 11 mode • TM 9, 1, 16 mode Ø Summary

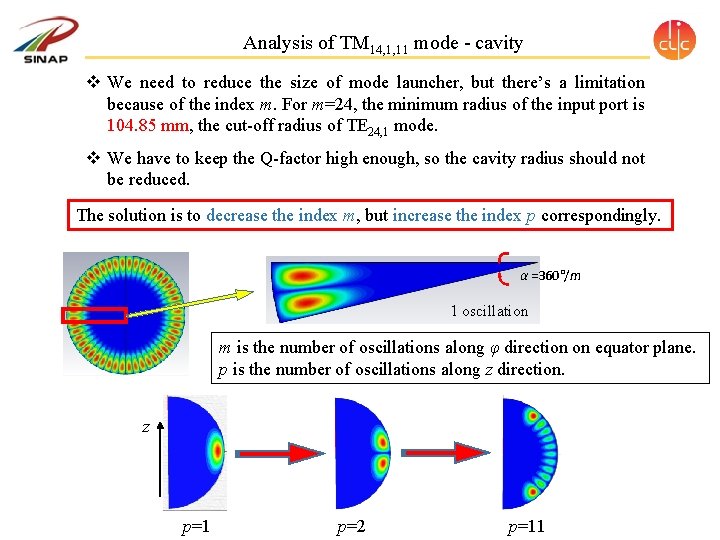
Analysis of TM 14, 1, 11 mode - cavity v We need to reduce the size of mode launcher, but there’s a limitation because of the index m. For m=24, the minimum radius of the input port is 104. 85 mm, the cut-off radius of TE 24, 1 mode. v We have to keep the Q-factor high enough, so the cavity radius should not be reduced. The solution is to decrease the index m, but increase the index p correspondingly. α =360°/m 1 oscillation m is the number of oscillations along φ direction on equator plane. p is the number of oscillations along z direction. z p=1 p=2 p=11

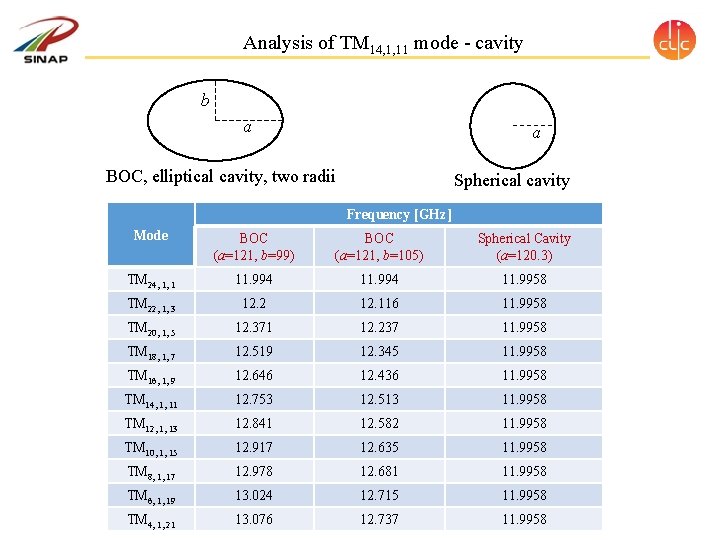
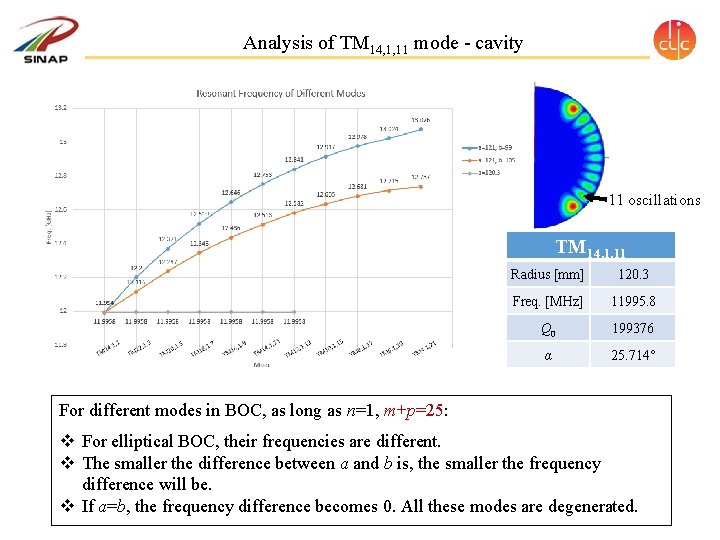
Analysis of TM 14, 1, 11 mode - cavity b a a BOC, elliptical cavity, two radii Spherical cavity Frequency [GHz] Mode BOC (a=121, b=99) BOC (a=121, b=105) Spherical Cavity (a=120. 3) TM 24, 1, 1 11. 994 11. 9958 TM 22, 1, 3 12. 2 12. 116 11. 9958 TM 20, 1, 5 12. 371 12. 237 11. 9958 TM 18, 1, 7 12. 519 12. 345 11. 9958 TM 16, 1, 9 12. 646 12. 436 11. 9958 TM 14, 1, 11 12. 753 12. 513 11. 9958 TM 12, 1, 13 12. 841 12. 582 11. 9958 TM 10, 1, 15 12. 917 12. 635 11. 9958 TM 8, 1, 17 12. 978 12. 681 11. 9958 TM 6, 1, 19 13. 024 12. 715 11. 9958 TM 4, 1, 21 13. 076 12. 737 11. 9958

Analysis of TM 14, 1, 11 mode - cavity 11 oscillations TM 14, 1, 11 Radius [mm] 120. 3 Freq. [MHz] 11995. 8 Q 0 199376 α 25. 714° For different modes in BOC, as long as n=1, m+p=25: v For elliptical BOC, their frequencies are different. v The smaller the difference between a and b is, the smaller the frequency difference will be. v If a=b, the frequency difference becomes 0. All these modes are degenerated.

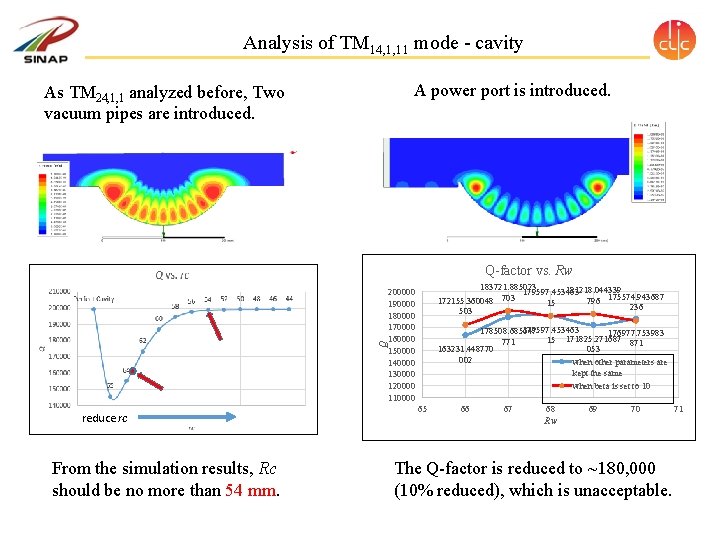
Analysis of TM 14, 1, 11 mode - cavity A power port is introduced. As TM 24, 1, 1 analyzed before, Two vacuum pipes are introduced. Q Q-factor vs. Rw reduce rc From the simulation results, Rc should be no more than 54 mm. 183721. 885023 181218. 044339 179597. 453463 172155. 360048 703 796 175574. 943687 15 236 503 200000 190000 180000 170000 160000 150000 140000 130000 120000 110000 179597. 453463 178508. 685647 176977. 753983 15 171825. 271687 871 771 163231. 448770 053 002 when other parameters are kept the same when beta is set to 10 65 66 67 68 69 70 Rw The Q-factor is reduced to ~180, 000 (10% reduced), which is unacceptable. 71

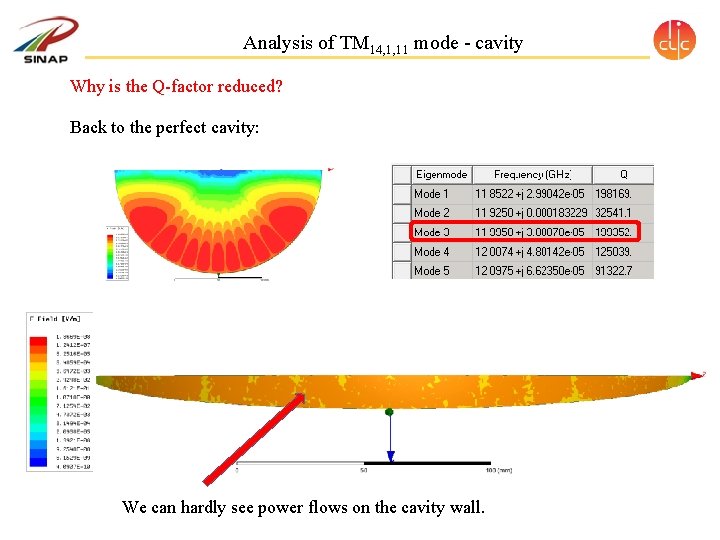
Analysis of TM 14, 1, 11 mode - cavity Why is the Q-factor reduced? Back to the perfect cavity: We can hardly see power flows on the cavity wall.

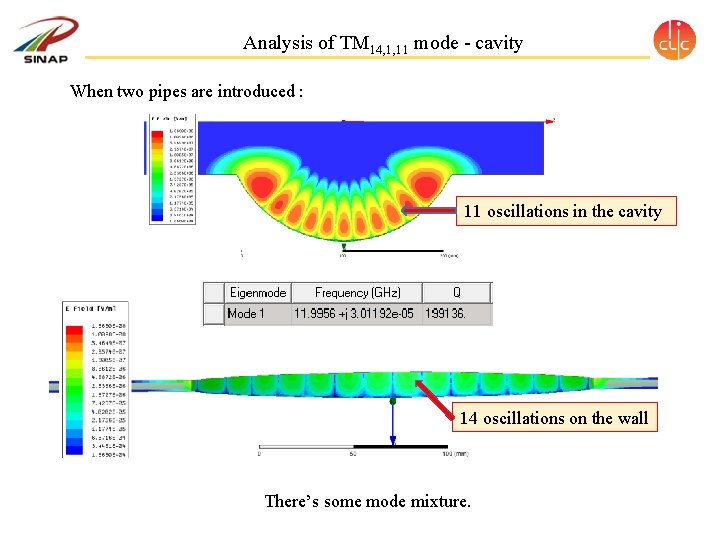
Analysis of TM 14, 1, 11 mode - cavity When two pipes are introduced : 11 oscillations in the cavity 14 oscillations on the wall There’s some mode mixture.

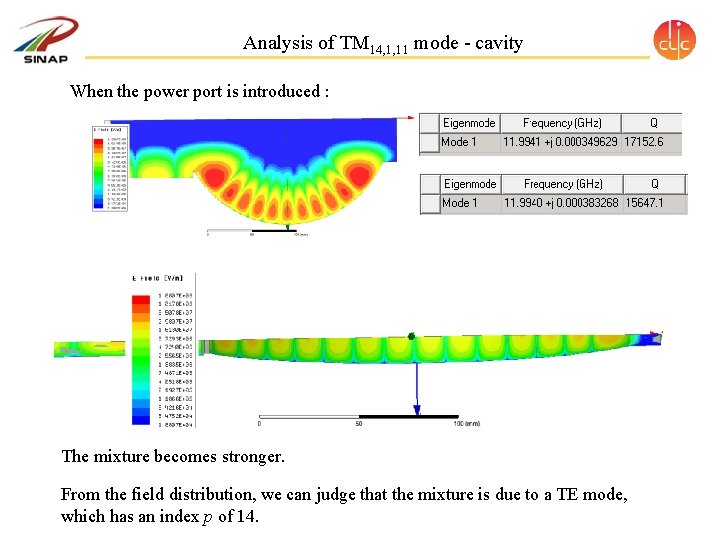
Analysis of TM 14, 1, 11 mode - cavity When the power port is introduced : The mixture becomes stronger. From the field distribution, we can judge that the mixture is due to a TE mode, which has an index p of 14.

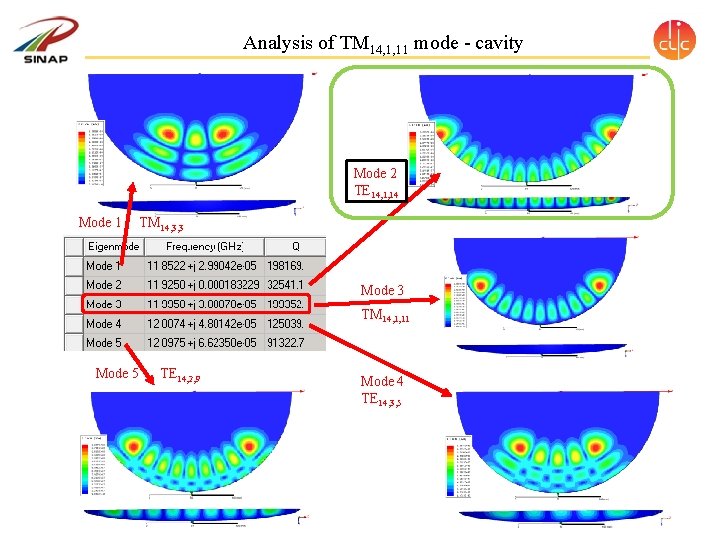
Analysis of TM 14, 1, 11 mode - cavity Mode 2 TE 14, 1, 14 Mode 1 TM 14, 3, 3 Mode 3 TM 14, 1, 11 Mode 5 TE 14, 2, 9 Mode 4 TE 14, 3, 5

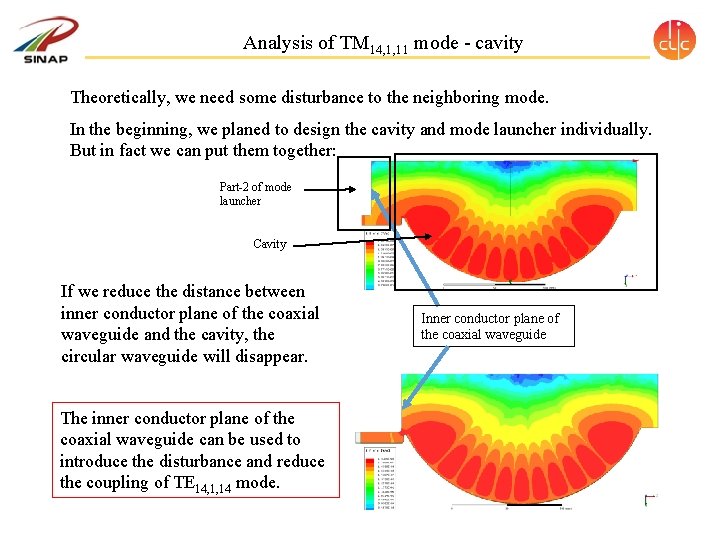
Analysis of TM 14, 1, 11 mode - cavity Theoretically, we need some disturbance to the neighboring mode. In the beginning, we planed to design the cavity and mode launcher individually. But in fact we can put them together: Part-2 of mode launcher Cavity If we reduce the distance between inner conductor plane of the coaxial waveguide and the cavity, the circular waveguide will disappear. The inner conductor plane of the coaxial waveguide can be used to introduce the disturbance and reduce the coupling of TE 14, 1, 14 mode. Inner conductor plane of the coaxial waveguide

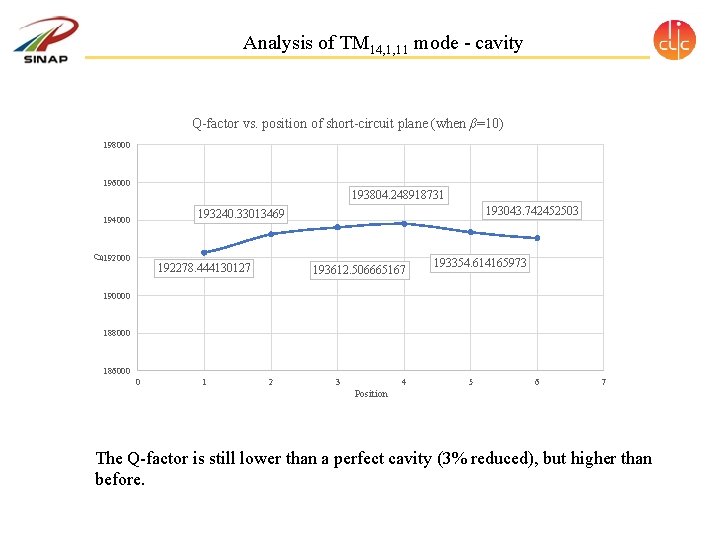
Analysis of TM 14, 1, 11 mode - cavity Q-factor vs. position of short-circuit plane (when β=10) 198000 196000 193804. 248918731 Q 193043. 742452503 193240. 33013469 194000 192278. 444130127 193612. 506665167 193354. 614165973 190000 188000 186000 0 1 2 3 4 5 6 7 Position The Q-factor is still lower than a perfect cavity (3% reduced), but higher than before.

Outline Ø Requirement Ø BOC Ø Analysis and RF design • TM 24, 1, 1 mode • TM 14, 1, 11 mode • TM 9, 1, 16 mode Ø Summary

Analysis of TM 9, 1, 16 mode The mode launcher is still too big. So we continue to reduce index m. But m cannot be too small, otherwise the surface field in mode launcher will be too high. Besides, the smaller the index m is, the more degenerated high-order modes there will be. For example: Working mode High-order modes TM 9, 1, 16 TM 18, 1, 7 TM 8, 1, 17 TM 16, 1, 9, TM 24, 1, 1 TM 7, 1, 18 TM 14, 1, 11, TM 21, 1, 4 TM 6, 1, 19 TM 12, 1, 13, TM 18, 1, 7, TM 24, 1, 1 TM 5, 1, 20 TM 10, 1, 15, TM 15, 1, 10, TM 20, 1, 5 For now, index m of 9 is chosen: Neighboring modes. TM 9, 1, 16

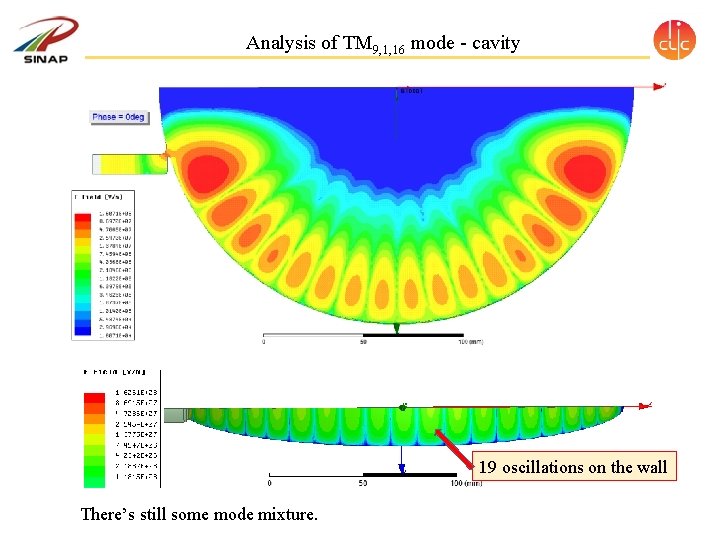
Analysis of TM 9, 1, 16 mode - cavity 19 oscillations on the wall There’s still some mode mixture.

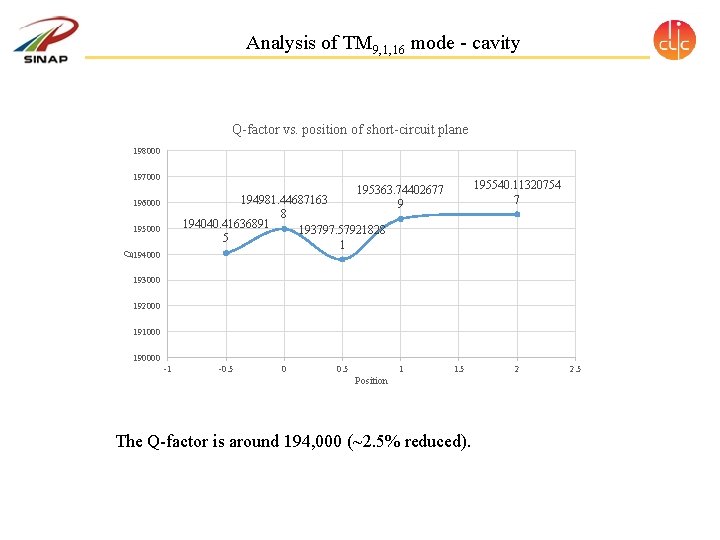
Analysis of TM 9, 1, 16 mode - cavity Q-factor vs. position of short-circuit plane 198000 197000 196000 195000 Q 195540. 11320754 7 195363. 74402677 194981. 44687163 9 8 194040. 41636891 193797. 57921828 5 1 194000 193000 192000 191000 190000 -1 -0. 5 0 0. 5 1 1. 5 Position The Q-factor is around 194, 000 (~2. 5% reduced). 2 2. 5

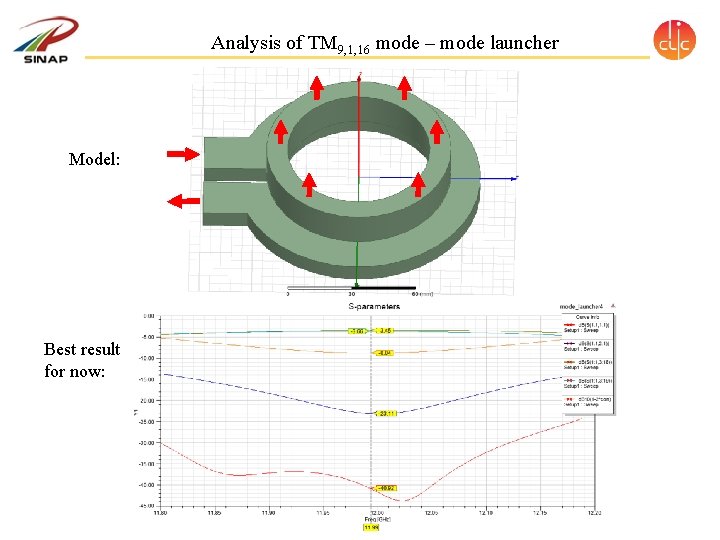
Analysis of TM 9, 1, 16 mode – mode launcher Model: Best result for now:

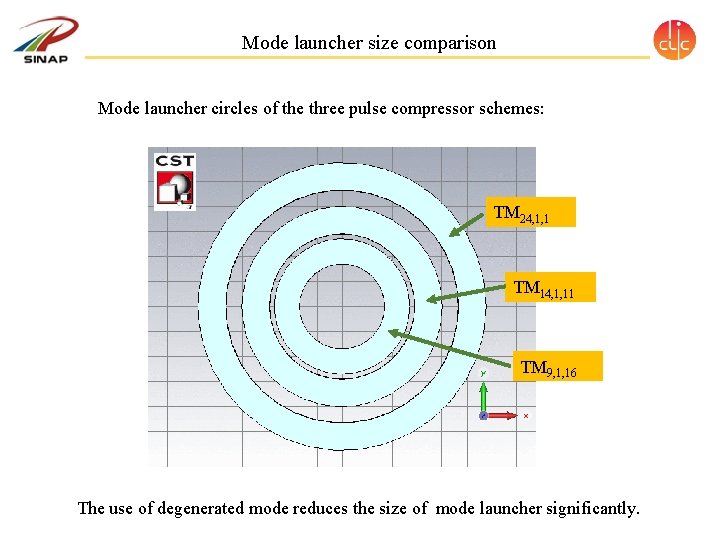
Mode launcher size comparison Mode launcher circles of the three pulse compressor schemes: TM 24, 1, 1 TM 14, 1, 11 TM 9, 1, 16 The use of degenerated mode reduces the size of mode launcher significantly.

Outline Ø Requirement Ø BOC Ø Analysis and RF design • TM 24, 1, 1 mode • TM 14, 1, 11 mode • TM 9, 1, 16 mode Ø Summary

Summary v This work is to design a spherical pulse compressor using degenerated “whispering gallery” mode. v Some investigations on “whispering gallery” mode and its degenerated modes are presented. v The structure is being designed. Some preliminary results are presented.

Thank you!