A New Model of Distributed Genetic Algorithm for

A New Model of Distributed Genetic Algorithm for Cluster Systems: Dual Individual DGA Tomoyuki HIROYASU Mitsunori MIKI Masahiro HAMASAKI Yusuke TANIMURA Doshisha University Kyoto, Japan

Cluster, Hyper Cluster, GRID Tasks Job A job of application should be divided into some tasks in several ways. GRID

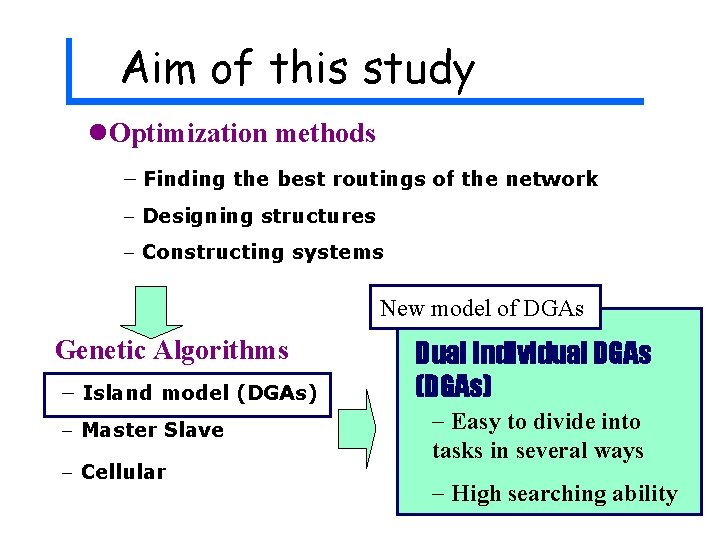
Aim of this study l. Optimization methods - Finding the best routings of the network - Designing structures - Constructing systems New model of DGAs Genetic Algorithms - Island model (DGAs) - Master Slave - Cellular Dual Individual DGAs (DGAs) - Easy to divide into tasks in several ways - High searching ability

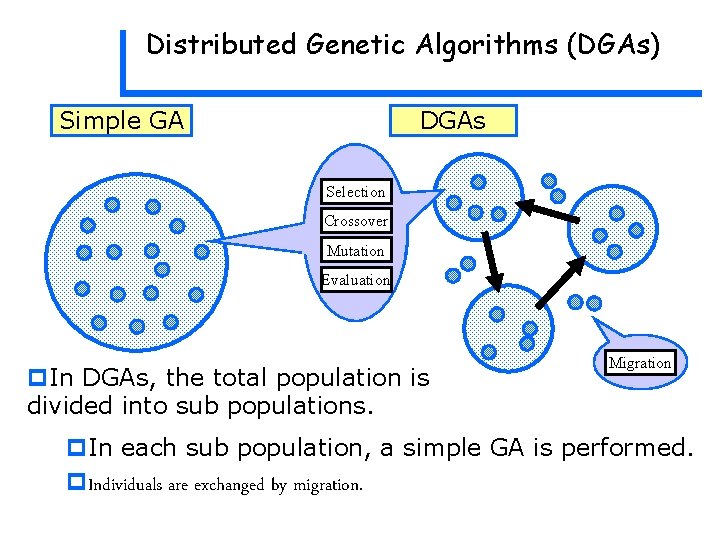
Distributed Genetic Algorithms (DGAs) Simple GA DGAs Selection Crossover Mutation Evaluation p. In DGAs, the total population is divided into sub populations. Migration p. In each sub population, a simple GA is performed. p. Individuals are exchanged by migration.

Related work p. There are several studies concerned with DGAs. p. It is reported that DGAs have high searching ability. “A survey of parallel distributed genetic algorithms” E. Alba and J. M. Troya “A survey of parallel genetic algorithms” E. Cantu-Paz “A Searching Ability of DGAs” M. Miki, T. Hiroyasu, M. Kaneko and K. Hatanaka

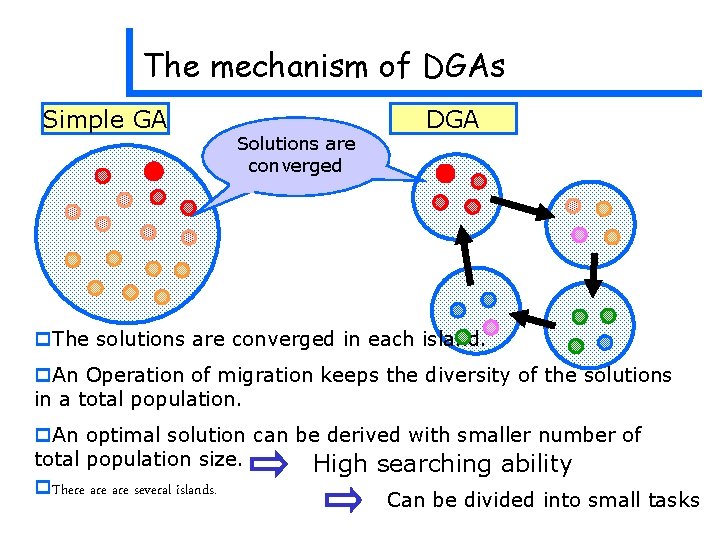
The mechanism of DGAs Simple GA Solutions are converged DGA p. The solutions are converged in each island. p. An Operation of migration keeps the diversity of the solutions in a total population. p. An optimal solution can be derived with smaller number of total population size. High searching ability p. There are several islands. Can be divided into small tasks

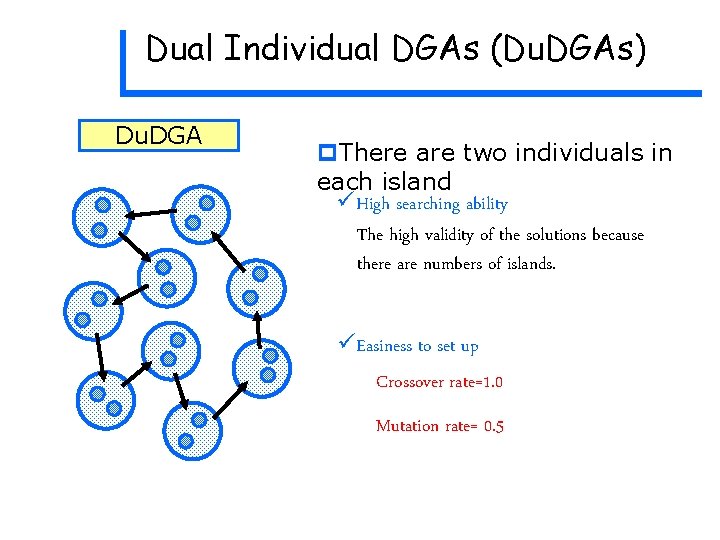
Dual Individual DGAs (Du. DGAs) Du. DGA p. There are two individuals in each island üHigh searching ability The high validity of the solutions because there are numbers of islands. üEasiness to set up Crossover rate=1. 0 Mutation rate= 0. 5

Operations of Du. DGAs Selection l. There are 4 individuals after the crossover (two parents and two children). l. One of the parents and one of the children are selected with respect to their fitness values. Migration l. Migrated Individual is chosen randomly. l. Migrated individual is copied and moved to the other islnads. l The existed individual that has smaller fitness value is over wrote by the migrated individual. Overwrite Copy

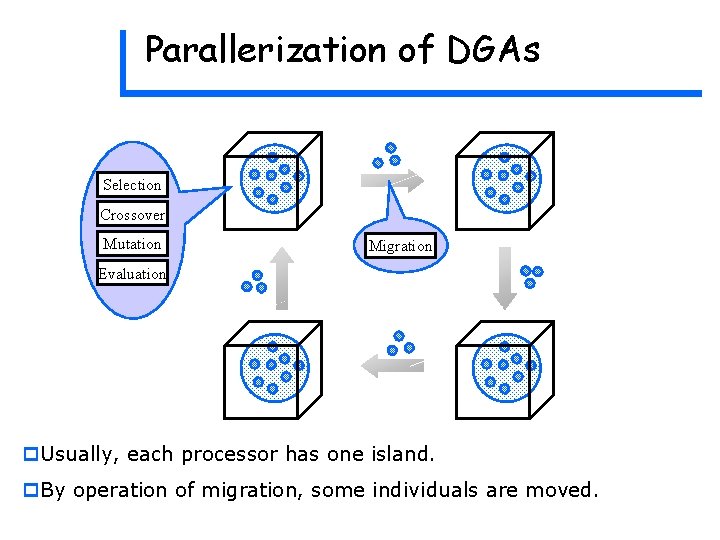
Parallerization of DGAs Selection Crossover Mutation Migration Evaluation p. Usually, each processor has one island. p. By operation of migration, some individuals are moved.

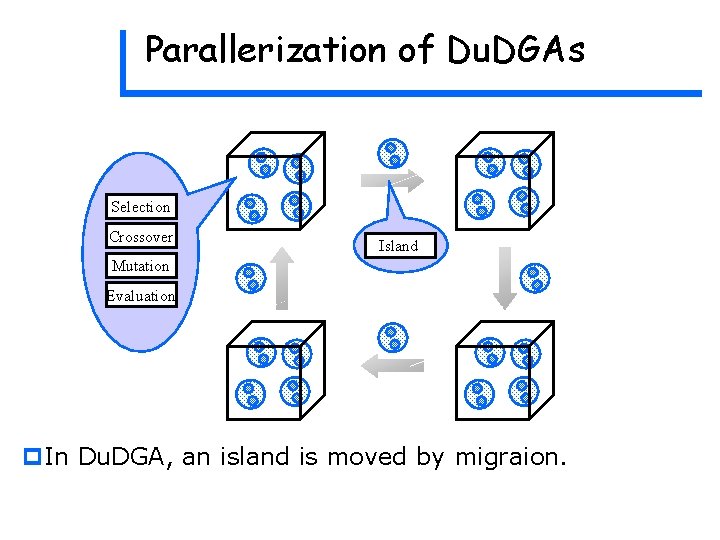
Parallerization of Du. DGAs Selection Crossover Island Mutation Evaluation p. In Du. DGA, an island is moved by migraion.

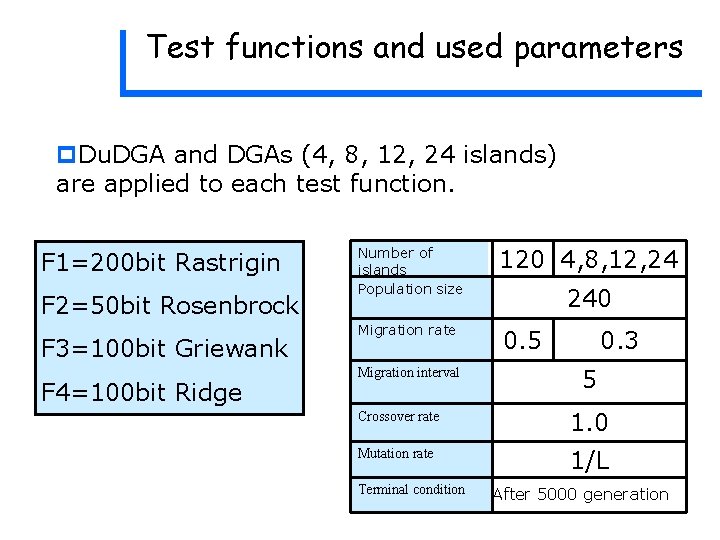
Test functions and used parameters p. Du. DGA and DGAs (4, 8, 12, 24 islands) are applied to each test function. F 1=200 bit Rastrigin F 2=50 bit Rosenbrock F 3=100 bit Griewank F 4=100 bit Ridge Number of islands Population size 120 4, 8, 12, 24 Migration rate 0. 5 Migration interval 240 0. 3 5 Crossover rate 1. 0 Mutation rate 1/L Terminal condition After 5000 generation

Test Functions Rastrigin Griewank Ridge Rosenbrok

Cluster system for calculation Spec. of Cluster (16 nodes) Processor Clock # Processors Main memory Network (100 Mbps) Communication OS Compiler PentiumⅡ(Deschutes) 400 MHz 1 × 16 128 Mbytes × 16 Fast Ethernet TCP/IP, MPICH 1. 1. 2 Linux 2. 2. 10 gcc (egcs-2. 91. 61)

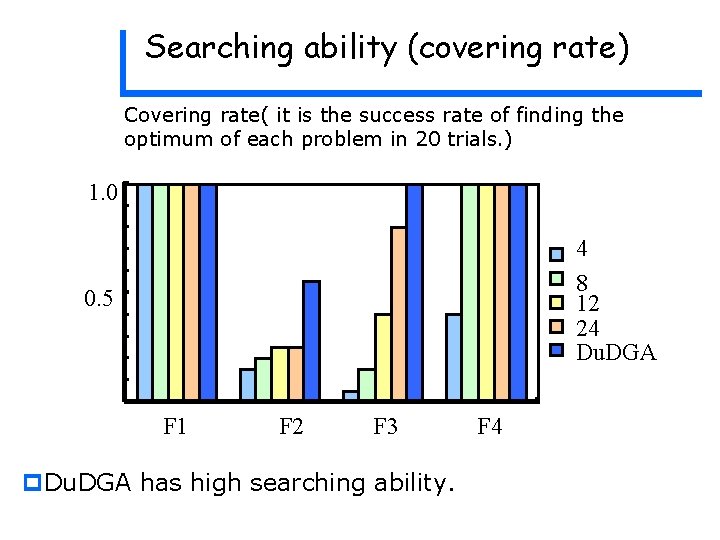
Searching ability (covering rate) Covering rate( it is the success rate of finding the optimum of each problem in 20 trials. ) 1. 0 4 8 12 24 Du. DGA 0. 5 F 1 F 2 F 3 p. Du. DGA has high searching ability. F 4

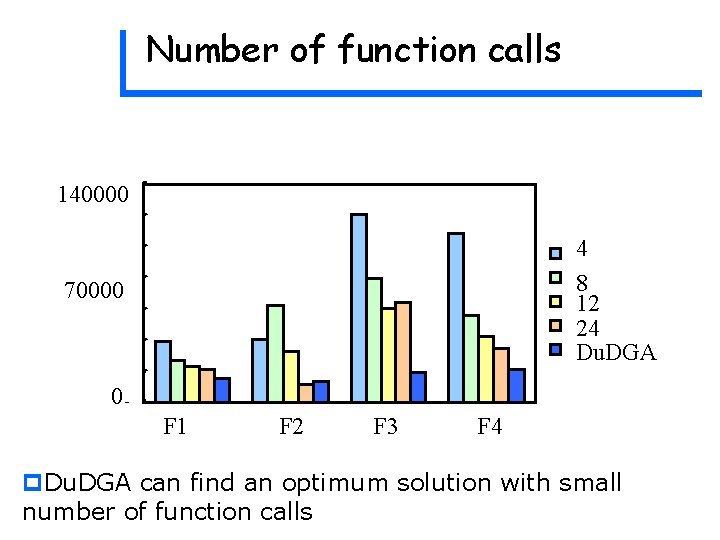
Number of function calls 140000 4 8 12 24 Du. DGA 70000 0 F 1 F 2 F 3 F 4 p. Du. DGA can find an optimum solution with small number of function calls

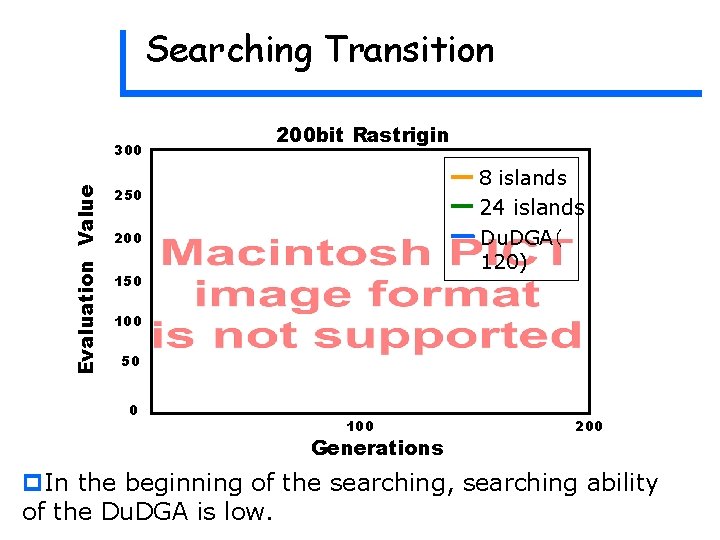
Searching Transition Evaluation Value 300 200 bit Rastrigin 8 islands 250 24 islands Du. DGA（ 120) 200 150 100 50 0 100 Generations 200 p. In the beginning of the searching, searching ability of the Du. DGA is low.

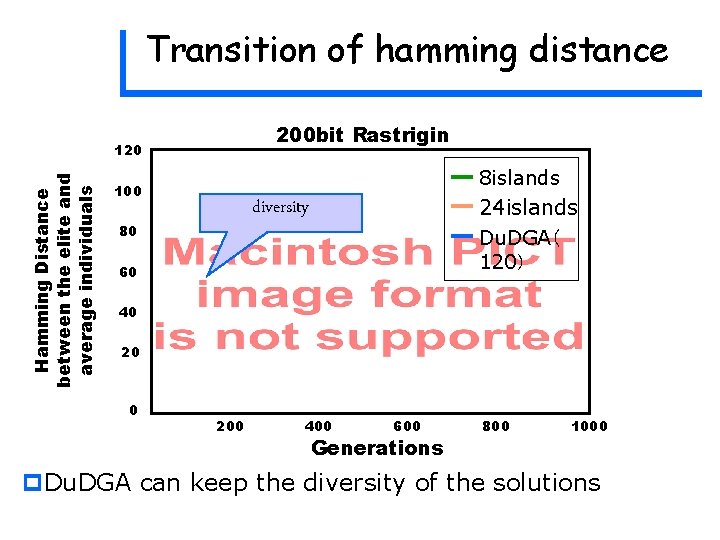
Transition of hamming distance 200 bit Rastrigin Hamming Distance between the elite and average individuals 120 8 islands 100 24 islands Du. DGA（ 120) diversity 80 60 40 200 400 600 Generations 800 1000 p. Du. DGA can keep the diversity of the solutions

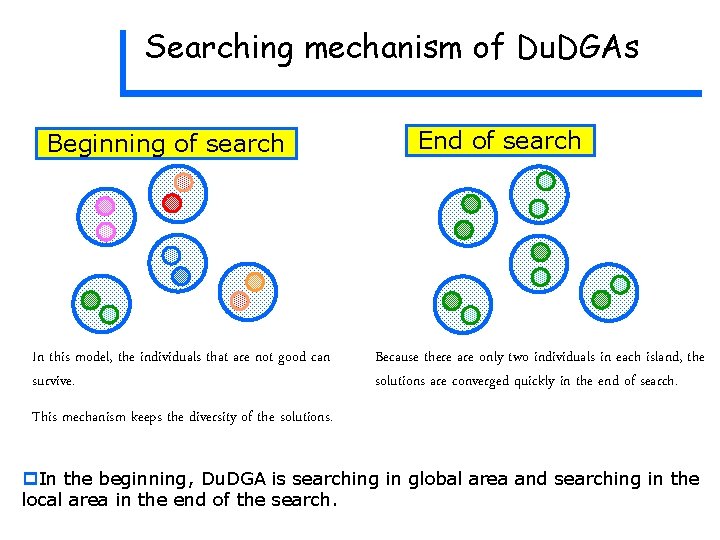
Searching mechanism of Du. DGAs Beginning of search In this model, the individuals that are not good can survive. End of search Because there are only two individuals in each island, the solutions are converged quickly in the end of search. This mechanism keeps the diversity of the solutions. p. In the beginning, Du. DGA is searching in global area and searching in the local area in the end of the search.

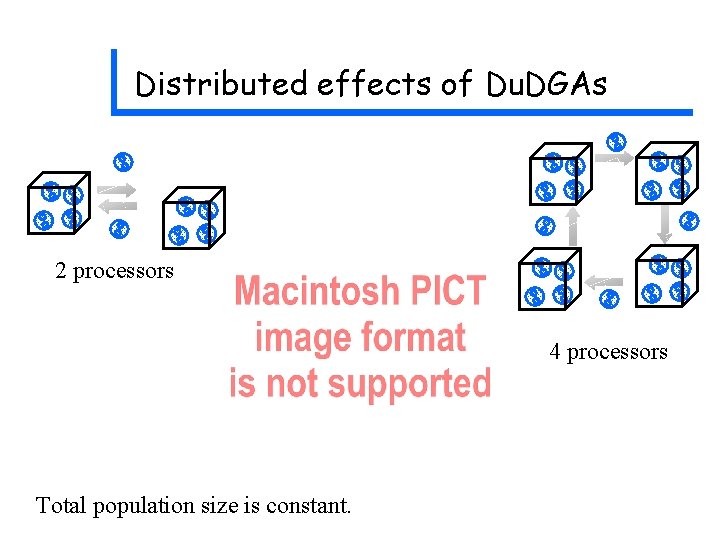
Distributed effects of Du. DGAs 2 processors 4 processors Total population size is constant.

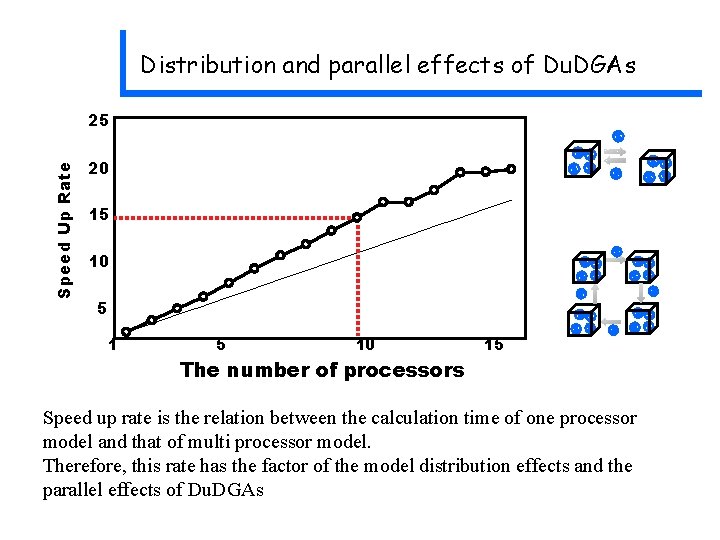
Distribution and parallel effects of Du. DGAs Speed Up Rate 25 20 15 10 The number of processors 15 Speed up rate is the relation between the calculation time of one processor model and that of multi processor model. Therefore, this rate has the factor of the model distribution effects and the parallel effects of Du. DGAs

Conclusions p. Dual Individual Distributed Genetic Algorithms (Du. DGAs) üHigh searching ability üSome parameters needless to be set üThere are many islands üDu. DGAs can be divided into several tasks in many ways p. Du. DGAs will be applied to GRID systems (may be CCGrid 2000).

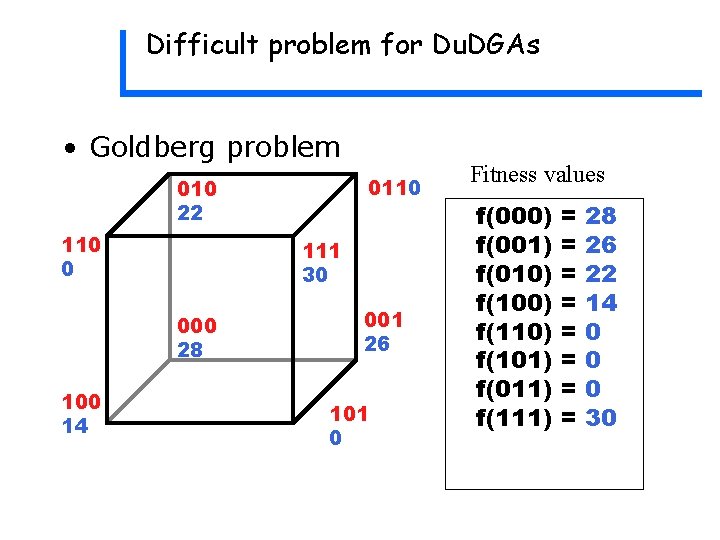
Difficult problem for Du. DGAs • Goldberg problem 0110 010 22 110 0 111 30 000 28 100 14 001 26 101 0 Fitness values f(000) f(001) f(010) f(100) f(110) f(101) f(011) f(111) = = = = 28 26 22 14 0 0 0 30