A new linear algorithm for checking a graph

A new linear algorithm for checking a graph for 3 -edge-connectivity Feng Sun Advisor: Committee: Dr. Robert W. Robinson Dr. E. Rodney Canfield Dr. Eileen T. Kraemer 2003. 2

Outline l l Overview Concepts and definitions Analysis of separation pairs Test results

Graph Connectivity l Applications l l l Network reliability Planar graph Vertex Connectivity (κ) Edge Connectivity (λ) Our algorithm l l l Check whether a graph is 3 -edge-connected in O(m+n) time Based on Depth-first search Modified from the algorithm of Hopcroft and Tarjan to divide a graph into 3 -vertex-connected components

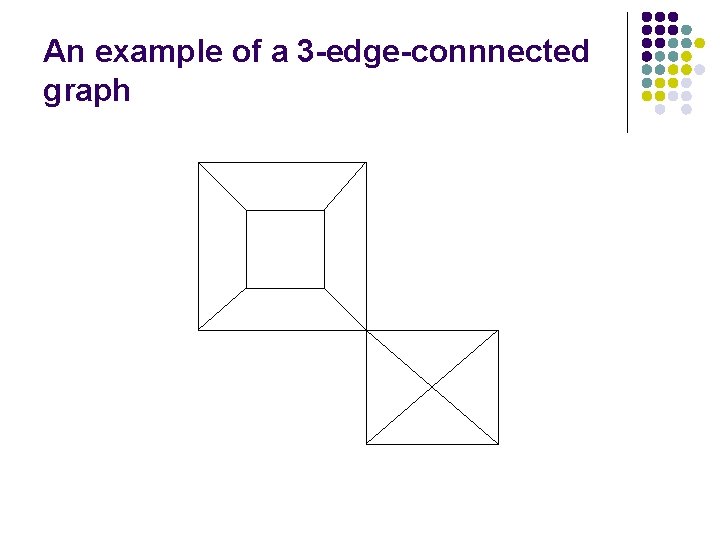
An example of a 3 -edge-connnected graph

Concepts l Graph l l Tree l l l An ordered pair of disjoint sets (V, E), where V is the vertex set and E is the edge set. E is a subset of the set V(2) of unordered pairs from V. The order of a graph is |V| and the size of a graph is |E|. A graph is labeled if the integers from 1 through n are assigned to its vertices. An unlabeled graph is an isomorphism class of labeled graphs. Acyclic connected graph A subgraph which contains all the vertices of a graph is the spanning tree of the graph Edge separator l l l A minimal edge set S such that removal of S from a graph G disconnect G. A graph is k-edge-connected if every edge-separator has at least k edges. The edge connectivity of a graph G of order n ≥ 2 is the minimum cardinality of an edge-separator.

Concepts (cont. ) l Palm tree l Let P be a directed graph consisting of two disjoint sets of edges denoted by v→w and v --→w. P is a palm tree if P satisfies the following properties: l l The subgraph T containing the edges v→w is a spanning tree of P. If v --→w, then w*→v. That is, each edge not in the spanning tree of P connects a vertex with one of its ancestors in T. The edges v --→w are called the fronds of P. 1 2 4 3

Depth-first Search ALGORITHM DFS(G) 1 FOR each vertex v in V(G) 2 NUMBER(v) = FATHER(v) = 0; 3 time = 0; 4 DFS-VISIT(root); END ALGORITHM PROCEDURE DFS-VISIT(v) 1 NUMBER(v) = time + 1 2 FOR w in the adjacency list of v DO 3 { 4 IF NUMBER(w) == 0 THEN 5 { 6 mark vw as a tree edge in P; 7 FATHER(w) = v; 8 DFS-VISIT(w); 9 } 10 ELSE IF NUMBER(w) < NUMBER(v) and w != FATHER(v) THEN 11 mark vw as a frond in P; 12 }

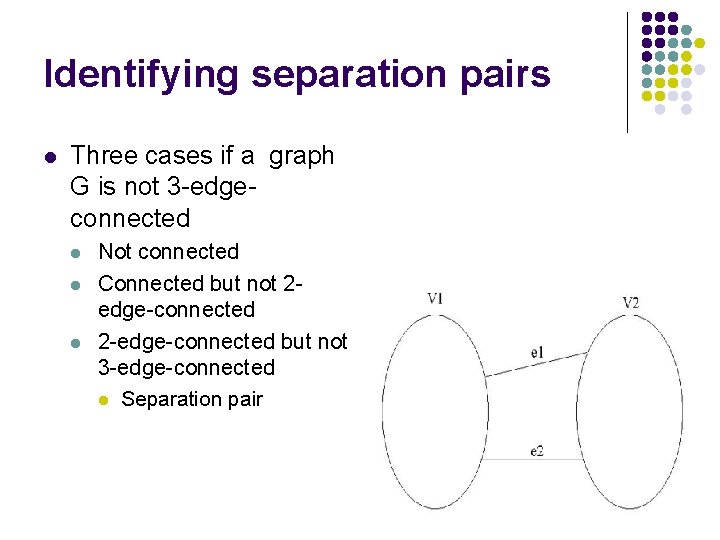
Identifying separation pairs l Three cases if a graph G is not 3 -edgeconnected l l l Not connected Connected but not 2 edge-connected 2 -edge-connected but not 3 -edge-connected l Separation pair

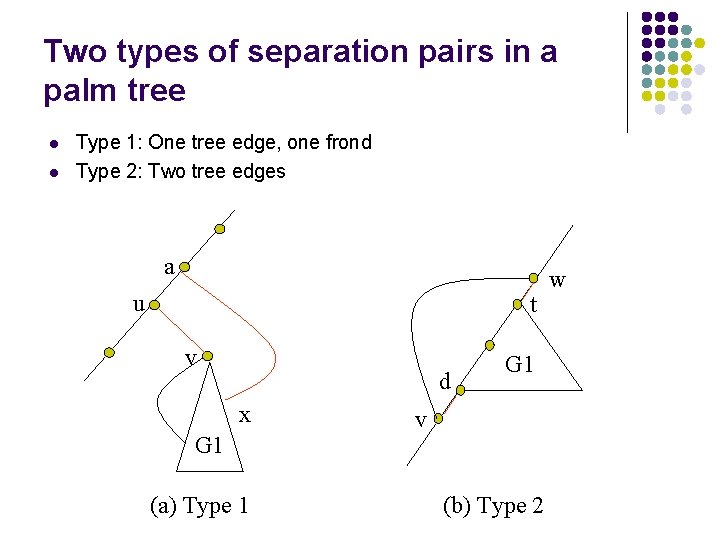
Two types of separation pairs in a palm tree l l Type 1: One tree edge, one frond Type 2: Two tree edges a u t v d x G 1 (a) Type 1 G 1 v (b) Type 2 w

Important values for identifying type 1 pair

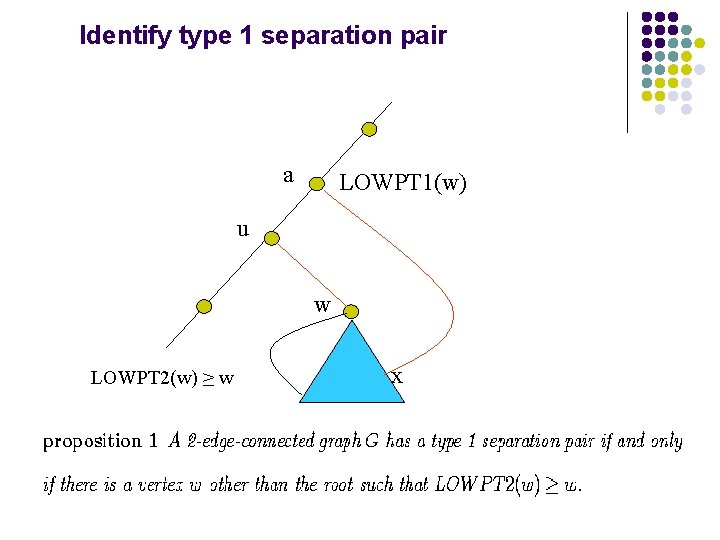
An Expanded DFS PROCEDURE FIRSTDFS-VISIT(v) 1 NUMBER(v) = time + 1; 2 LOWPT 1(v) = LOWPT 2(v) = NUMBER(v); 3 ND(v) = 1; 4 FOR w in the adjacency list of v DO 5 { 6 IF NUMBER(w) == 0 THEN 7 { 8 mark vw as a tree edge in P; 9 FATHER(w) = v; 10 FIRSTDFS-VISIT(w); 10. 1 IF ( LOWPT 1(w) < v and LOWPT 2(w) >= w ) THEN 10. 2 detect a type 1 separation pair, procedure stop; 11 IF LOWPT 1(w) < LOWPT 1(v) THEN 12 { 13 LOWPT 2(v) = MIN{LOWPT 1(v), LOWPT 2(w)}; 14 LOWPT 1(v) = LOWPT 1(w); 15 } 16 ELSE IF LOWPT 1(w) == LOWPT 1(v) THEN 17 LOWPT 2(v) = LOWPT 1(w); 18 ELSE 19 LOWPT 2(v) = MIN{LOWPT 2(v), LOWPT 1(w)}; 20 ND(v) = ND(v) + ND(w); 21 } 22 ELSE IF NUMBER(w) < NUMBER(v) and w != FATHER(v) THEN 23 { 24 mark vw as a frond in P; 25 IF NUMBER(w) < LOWPT 1(v) THEN 26 { 27 LOWPT 2(v) = LOWPT 1(v); 28 LOWPT 1(v) = NUMBER(w); 29 } 30 ELSE IF NUMBER(w) == LOWPT 1(v) THEN 31 LOWPT 2(v) = NUMBER(w); 32 ELSE 33 LOWPT 2(v) = MIN{LOWPT 2(v), NUMBER(w)}; 34 } 35 }

Identify type 1 separation pair a LOWPT 1(w) u w LOWPT 2(w) ≥ w x

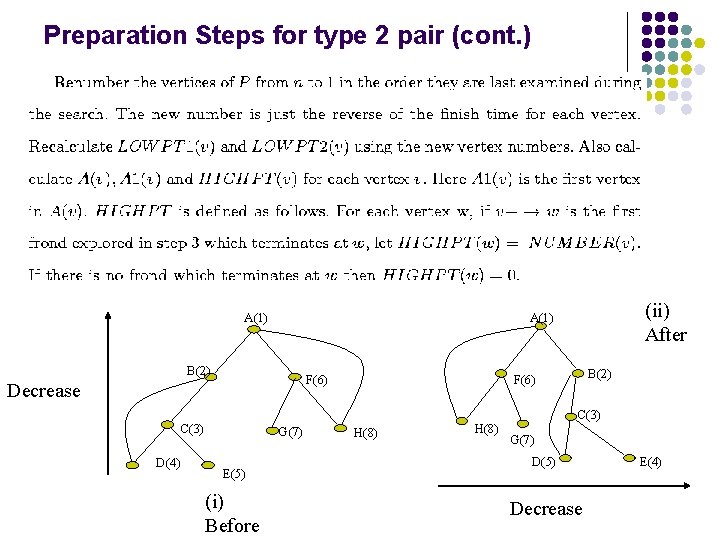
Preparation steps for type 2 pair

Preparation Steps for type 2 pair (cont. ) A(1) B(2) F(6) Decrease C(3) D(4) G(7) E(5) (i) Before (ii) After A(1) B(2) F(6) H(8) C(3) G(7) D(5) Decrease E(4)

Properties of the palm tree

Identify type 2 separation pair 1 u a 2 v y 2 b 3 y 1 x 2 x 1

Step to identify type 2 pair

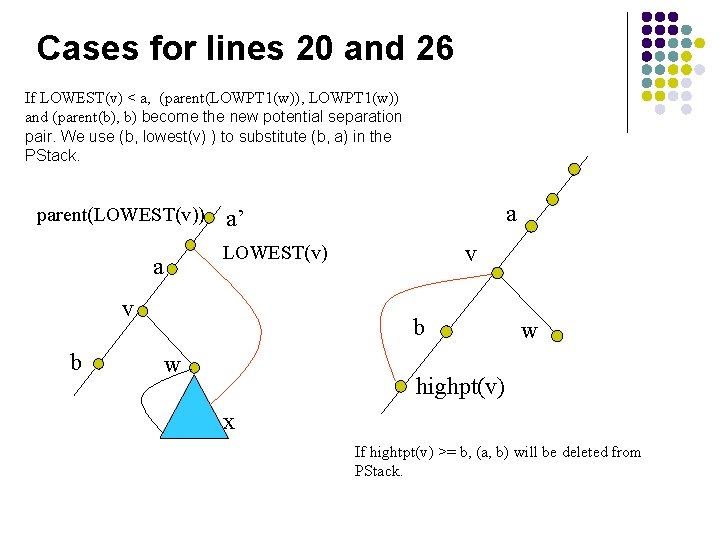
The DFS to identify type 2 pair PROCEDURE PATHSEARCH-DFS(v) (input: vertex v is the current vertex in the depth-first search) 1 FOR w IN A(v) DO 2 { 3 IF vw is a tree edge THEN 4 { 5 IF vw is a first edge of a path THEN 6 { 7 IF LOWPT 1(w) < LOWEST(v) and w is not A 1(v) THEN 8 LOWEST(v) = LOWPT 1(w); 9 add end-of-stack marker to PStack; 10 } 11 return. Val = PATHSEARCH-DFS(w); 12 IF return. Val == 0 THEN 13 return 0; 14 } 15 ELSE // vw is a frond 16 IF NUMBER(w) < LOWEST(v) THEN 17 LOWEST(v) = NUMBER(w); 18 } 19 WHILE (a, b) on PStack satisfies a <= NUMBER(v) < b and LOWEST(v) < a 20 remove (a, b) from PStack; 21 IF no pair deleted from PStack THEN 22 add ( LOWEST(v), A 1(v) ) to PStack; 23 IF (a, b) is the last pair deleted from PStack THEN 24 add ( LOWEST(v), b ) to PStack; 25 WHILE (a, b) on PStack satisfies a <= NUMBER(v) < b and HIGHPT(v) >= b 26 remove (a, b) from PStack; 27 WHILE (a, b) on PStack satisfies a = v 28 { 29 IF ( b <= a or a == 0 ) THEN 30 delete (a, b) from PStack; 31 ELSE //we find type 2 pair {(FATHER(a), (FATHER(b), b)} 32 return 0; 33 } 34 IF ( FATHER(v), v) is a first edge of a path THEN 35 delete all entries on PStack down to and including end-of-stack marker; 36 return 1;

Cases for lines 20 and 26 If LOWEST(v) < a, (parent(LOWPT 1(w)), LOWPT 1(w)) and (parent(b), b) become the new potential separation pair. We use (b, lowest(v) ) to substitute (b, a) in the PStack. parent(LOWEST(v)) v LOWEST(v) a v b a a’ b w w highpt(v) x If hightpt(v) >= b, (a, b) will be deleted from PStack.

Implementation and Test Results l General graph l Check graphs generated by Nauty l l l Numbers of labeled and unlabeled 3 -edge-connected graphs up to order 11. Numbers of labeled and unlabeled 3 -edge-connected blocks up to order 11. The above numbers for labeled graphs and for unlabeled 3 -edge-connected blocks were provided by S. K. Pootheri. Compare with Z. Chen’s algorithm for higher order random graphs Feynman diagrams l Compare with Qun Wang’s quadratic algorithm 0 1 2 3 4 5

Numbers of unlabeled and labeled 3 -edgeconnected graphs by order n

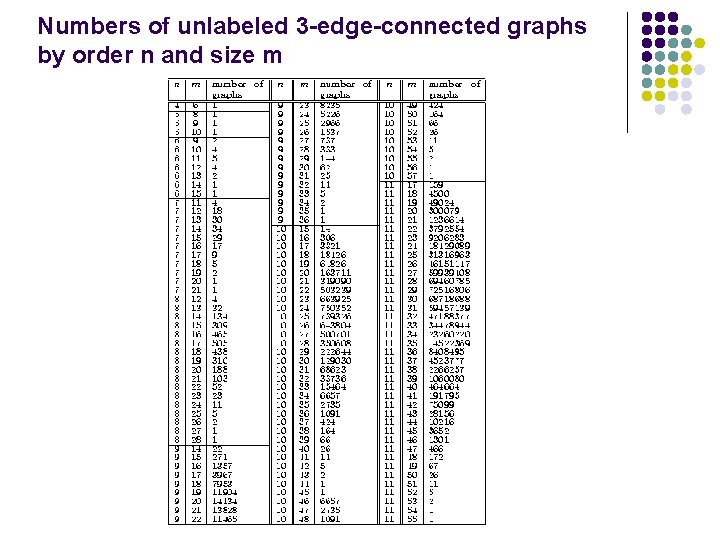
Numbers of unlabeled 3 -edge-connected graphs by order n and size m

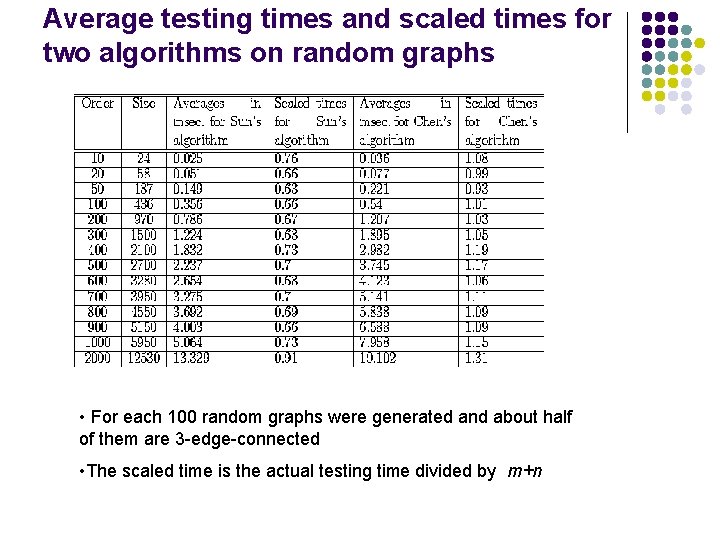
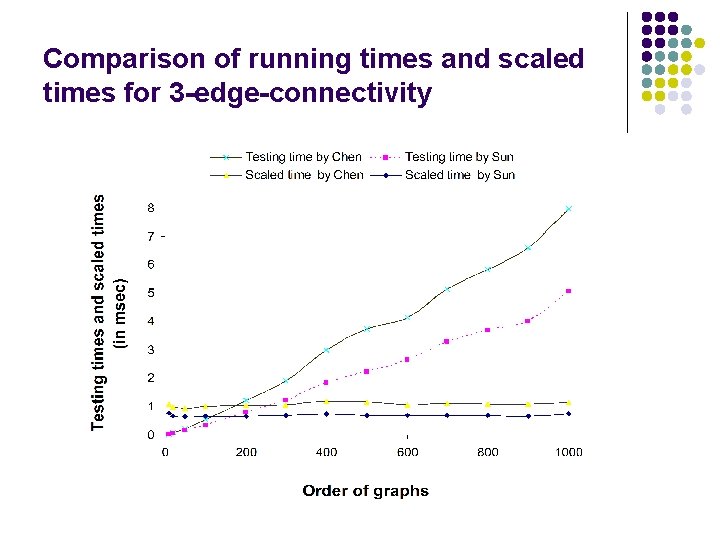
Average testing times and scaled times for two algorithms on random graphs • For each 100 random graphs were generated and about half of them are 3 -edge-connected • The scaled time is the actual testing time divided by m+n

Comparison of running times and scaled times for 3 -edge-connectivity

Comparison of running times for our linear algorithm and a quadratic algorithm on Feynman diagrams l l l Use a simplified algorithm for Feynman diagrams were generated by a program wrote by Dr. Robinson Q. Wang developed three algorithm for testing 3 -edge-connectivity of a Feynman diagram. The quadratic algorithm is the best for order less than 12

Conclusions and future work l l A new linear algorithm for determining whether a graph is 3 -edge-connected is presented. A variation of the algorithm was developed specifically for testing Feynman diagrams. Tests showed that the implementations are correct and also faster than the available alternatives. A promising future direction is to extend our algorithm to deal with fully dynamic 3 -edgeconnectivity problem.

Acknowledgements l l l Dr. Robert W. Robinson Dr. E. Rodney Canfield Dr. Eileen T. Kraemer Dr. David K. Lowenthal Other professors, staffs and students in our department