A MULTIPATH SPARSE BEAMFORMING METHOD AFSANEH ASAEI JOINT

A MULTIPATH SPARSE BEAMFORMING METHOD AFSANEH ASAEI JOINT WORK WITH: BARAN GÖZCÜ, VOLKAN CEVHER, MOHAMMAD J. TAGHIZADEH, BHIKSHA RAJ, HERVE BOURLARD
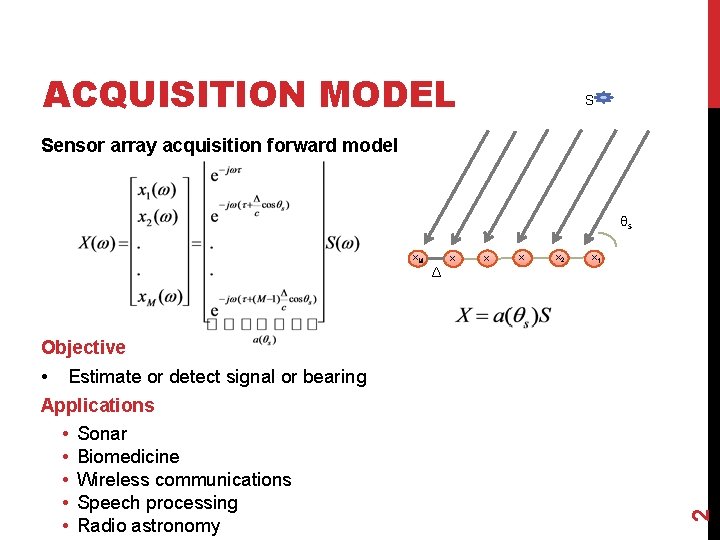
ACQUISITION MODEL S Sensor array acquisition forward model θs x. M Δ x. x. x 2 x 1 • Estimate or detect signal or bearing Applications • Sonar • Biomedicine • Wireless communications • Speech processing • Radio astronomy 2 Objective

PRIOR ART Ø A. C. Gurbuz, J. H. Mc. Clellan and Volkan Cevher, “A compressive beamforming method”, ICASSP 2008. Ø Y. Zhang, B. P. Ng and Q. Wan, “Sidelobe suppression for adaptive beamforming with sparse constraint on beam pattern”, Electronic Letters 2008. Ø Sergiy Vorobyov 3 Ø Yonina’s book
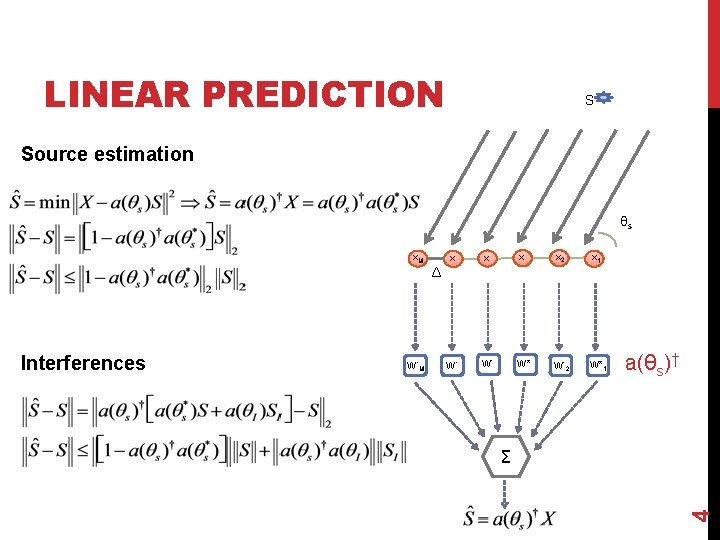
LINEAR PREDICTION S Source estimation θs Interferences W*M Δ x. x. x 2 x 1 W*. W*2 W*1 a(θs)† Σ 4 x. M
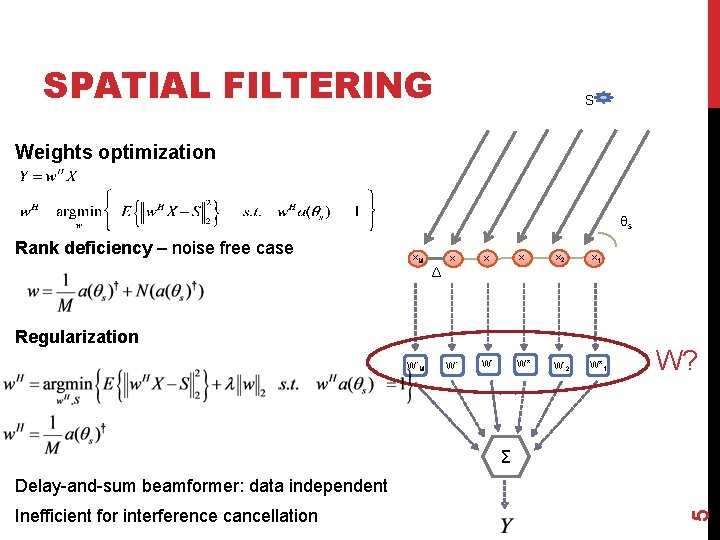
SPATIAL FILTERING S Weights optimization θs Rank deficiency – noise free case x. M Δ x. x. x 2 x 1 W*. W*2 W*1 Regularization W*M W? Σ Inefficient for interference cancellation 5 Delay-and-sum beamformer: data independent

SPARSE BEAMFORMER MVDR beamformer • Empirical risk minimization Regularization Analysis sparsity Synthesis sparsity Wavenumber Dictionary 6 • •
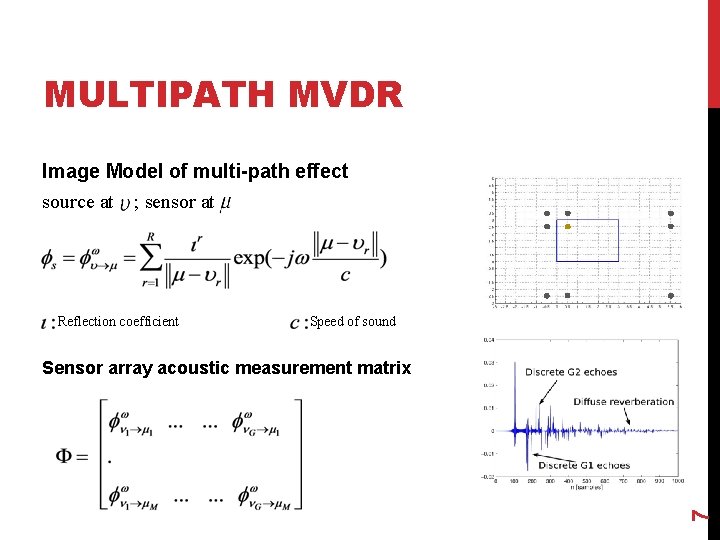
MULTIPATH MVDR Image Model of multi-path effect source at ; sensor at Reflection coefficient Speed of sound 7 Sensor array acoustic measurement matrix

SPARSE MULTIPATH MVDR Forward model of array acquisition Regularization on channel dictionary: channel-aware beamforming 8 Interference cancellation

ROBUSTNESS PRINCIPLE Regularization (diagonal loading) Eigenspace projection Worst case optimization 9 Little-info sector-based

NUMERICAL EVALUATIONS Beampattern and signal estimation • • • Deep nulls Sidelobe levels Sensitivity to steering angle mismatch Limited number of snapshots Wavefront distortion (local scattering) Test scenarios Far-field • • Reverberant • • • Uniform linear array Narrowband signal (freq. of 1024 sampled at 16 k. Hz) 5% random sample out of 1000 samples Circular array – RT 60 ≅ 300 ms 1000 speech frames SNR = 20 d. B 10 •
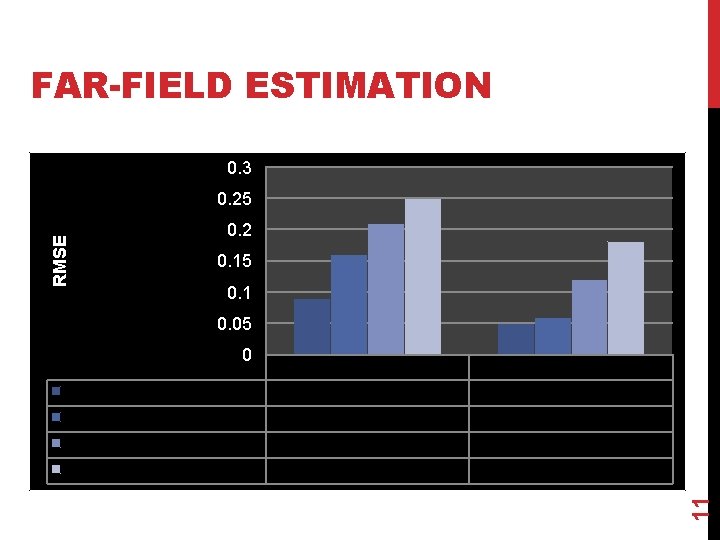
FAR-FIELD ESTIMATION 0. 3 RMSE 0. 25 0. 2 0. 15 0. 1 0. 05 Source + Noise Source + 1 Interference Source + 2 Interferences Source + 3 Interferences MVDR 0. 09 0. 16 0. 21 0. 25 Sparse MVDR 0. 05 0. 06 0. 12 0. 18 11 0
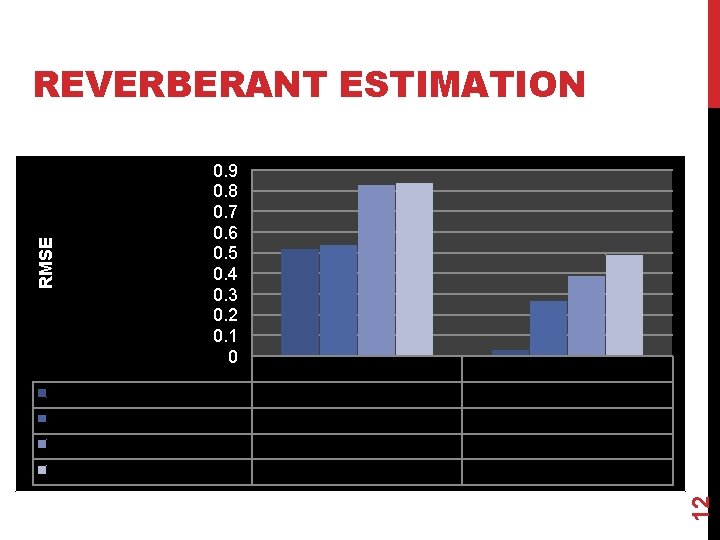
0. 9 0. 8 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0 Source + Noise Source + 1 Interference Source + 2 Interferences Source + 3 Interferences MVDR 0. 52 0. 54 0. 83 0. 84 Sparse MVDR 0. 03 0. 27 0. 39 0. 49 12 RMSE REVERBERANT ESTIMATION
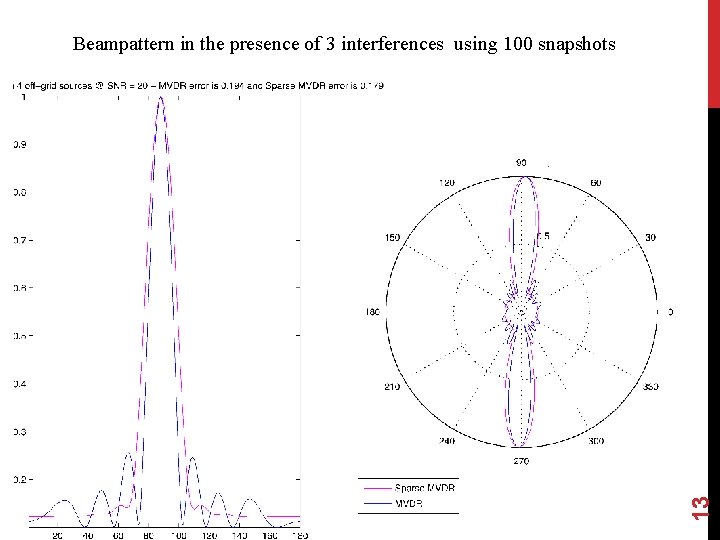
13 Beampattern in the presence of 3 interferences using 100 snapshots
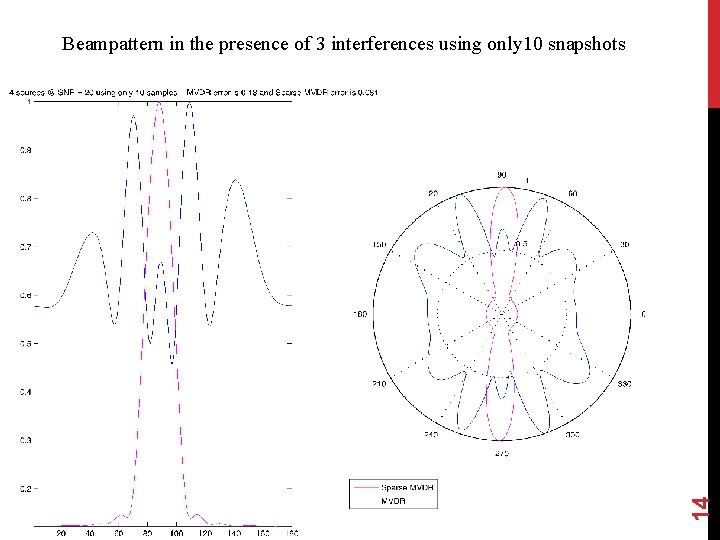
14 Beampattern in the presence of 3 interferences using only 10 snapshots
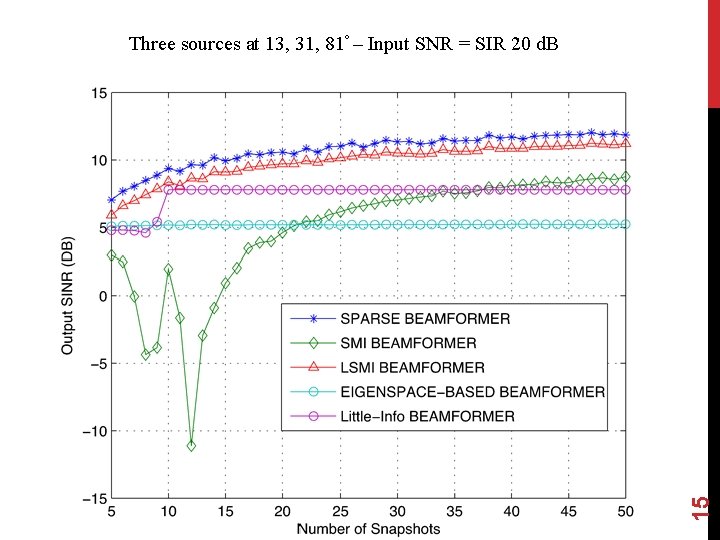
15 Three sources at 13, 31, 81º – Input SNR = SIR 20 d. B
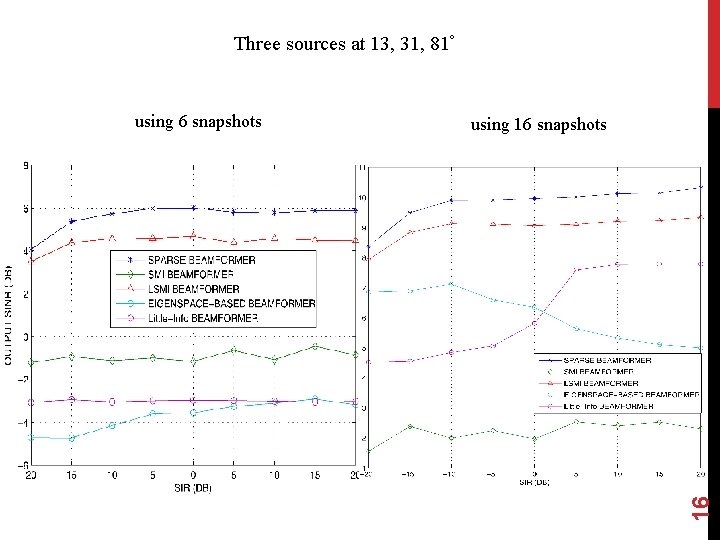
Three sources at 13, 31, 81º using 16 snapshots 16 using 6 snapshots
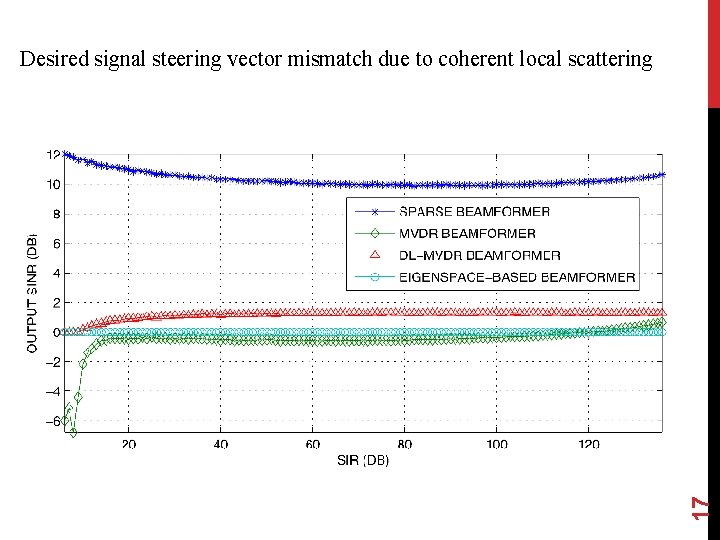
17 Desired signal steering vector mismatch due to coherent local scattering

CONCLUSION Ø Multipath beamforming for acoustic-informed spatial filtering Ø Improves reverberant acquisition Ø Enables acoustic calibration framework Sparse beamforming enables robust spatial filtering Ø Rapid convergence rate in adaptive arrays Ø Interference cancellation Ø Effect of correlation among signal and interference Ø Improved performance in mismatch condition Further extensions Ø Ø Ø Atomic norm minimization for infinite/continuous dictionary Regularization parameter 18 Ø

THANK YOU! 19 Questions?
- Slides: 19