A MODEL OF TROPICAL OCEANATMOSPHERE INTERACTION Julian Mc

A MODEL OF TROPICAL OCEAN-ATMOSPHERE INTERACTION Julian Mc Creary, Jr. Elsa Nickl Andreas Münchow

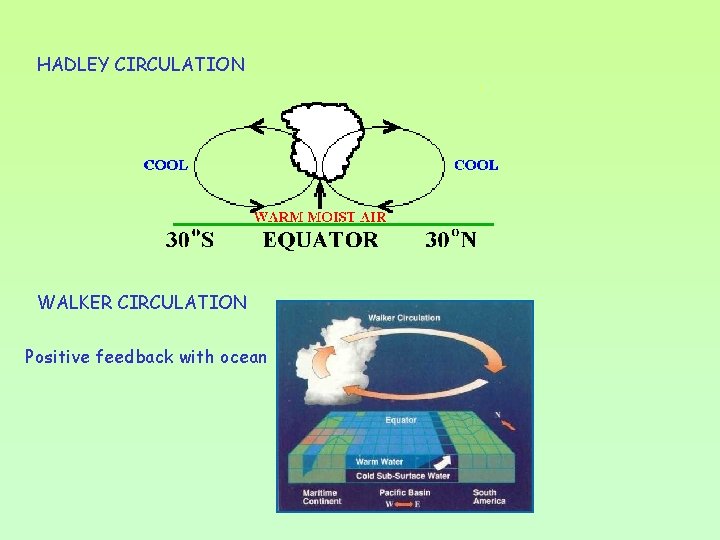
OBJECTIVE: A coupled ocean-atmosphere model is used to simulate long time scales systems like the Southern Oscillation (SO) HYPOTHESIS: The interaction ocean-atmosphere forms a coupled system with scale of 2 -9 years • Atmospheric models: rapid adjustment to a SST change • Ocean models: react radiating baroclinic Rossby waves The model takes account the atmosphere-ocean interaction suggested by Bjerknes (1966) for the Tropical Pacific: Hadley and Walker circulation

HADLEY CIRCULATION WALKER CIRCULATION Positive feedback with ocean

MODEL DESCRIPTION: Model ocean Model atmosphere Adjustment to equilibrium Oscillation conditions MODEL OCEAN Baroclinic mode of a two-layer ocean ~ gravest baroclinic mode of a continuosly stratified ocean h + Linear equations: x-mom: ut - yv + px = F + h ²u y-mom: vt - yu + py = G + h ²v F = x /H G = y /H h= H + p/g’ continuity: pt/c² + ux +vy =0 p=g’ (h-H) pt= (g’ (h-H)) = g’ h = w c² c² t g’ H t H Parameters: = 2 x 10 -11 m-1 s-1 H =100 m g’ =0. 02 ms-2 h = 104 m 2 s-1 c=2. 5 m/s

MODEL OCEAN Thermodynamics parametrization: SST warm, h>=hc cool, h< hc hc: upwelling along equator and eastern boundary (unspecified) OCEAN REGION: Tropical Pacific L (4500 km) EQ (0) 0 -L (4500 km) D (10, 000 km)

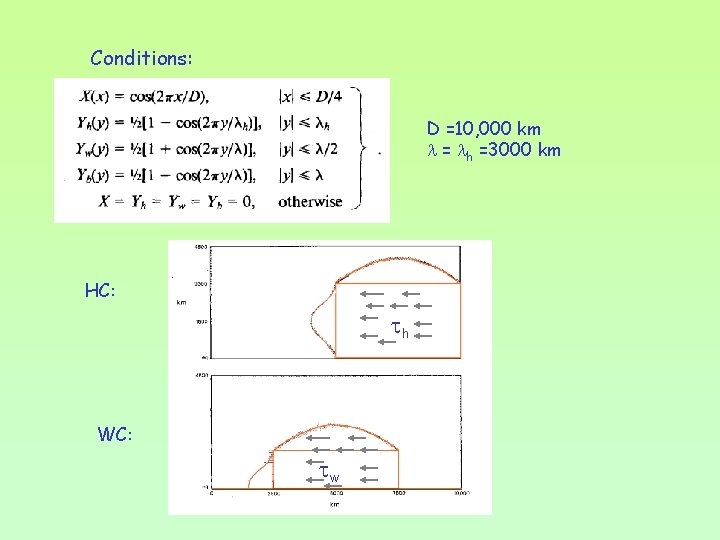
MODEL OCEAN Boundary conditions: u = v= 0 at sidewalls uy = v = 0 at equator Solutions for these conditions: Northern Hemisphere (Gent and Semter, 1980) MODEL ATMOSPHERE Wind field equations (3 patches of zonal wind stress): h: strenghtened HC w: well developed WC b: steady Pacific trade winds xh: 7500 km xw=xb: 5000 km

Conditions: D =10, 000 km = h =3000 km HC: h WC: w

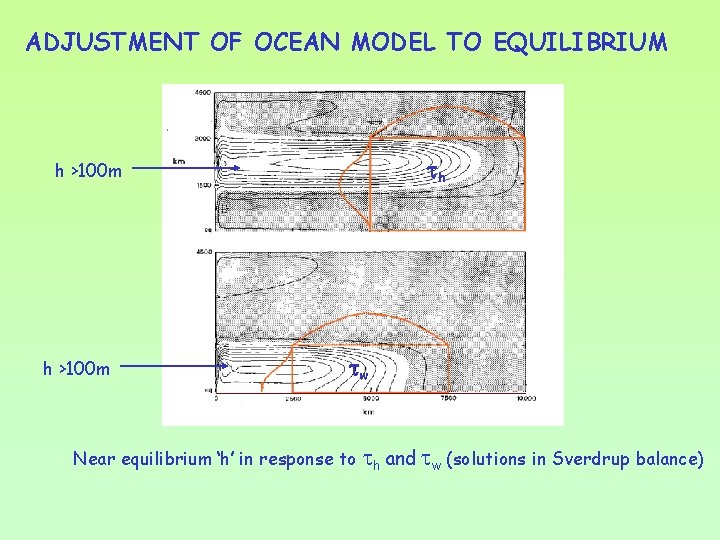
ADJUSTMENT OF OCEAN MODEL TO EQUILIBRIUM h h >100 m w Near equilibrium ‘h’ in response to h and w (solutions in Sverdrup balance)

ADJUSTMENT OF OCEAN MODEL TO EQUILIBRIUM • Rossby and Kelvin waves radiate from patch. The response of ocean to wind is basinwide • Kelvin: c At equator • Rossby: c/3 c = c²/( y²) farther from equator Equatorial winds: rapid adjustment t = 4 x/c t ~ 6 months Extra-equatorial winds: gradual adjustment t = ( xy²)/c² For minimum curl region related with h : t~ 4 years

ADJUSTMENT OF OCEAN MODEL TO EQUILIBRIUM • Sverdrup balance: good approximation for equilibrium state p: constant to be determined p is related to h: h= H + p/g’ h: equilibrium thickness at eastern boundary

OSCILLATION CONDITIONS 1. WC positive feedback hw < H feedback condition Initially he < H (SST cold in eastern ocean) WC switches on If hw < H holds ocean will adjust so he is even shallower 2. Requires HC, system does not reach equilibrium hbh < hc < hbw condition (model can never reach a state of equilibrium) hbh = equilibrium depth at eastern boundary in response to b and w hbw = equilibrium depth at eastern boundary in response to b and w

Initially he > hc (SST warm in eastern ocean) HC switches on he adjusts to hbh < hc (SST cold in eastern ocean) HC swithces off Condition hh < hw puts severe limits for oscillation It is required that h raises the model interface (h smaller) In eastern ocean more than w does

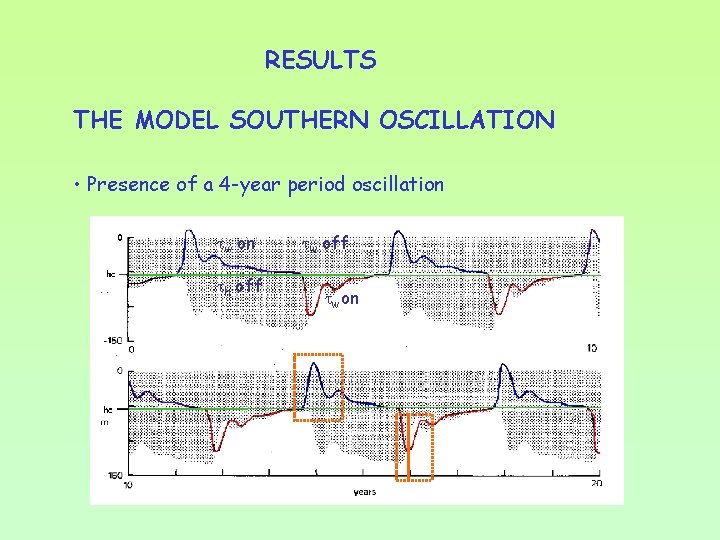
RESULTS THE MODEL SOUTHERN OSCILLATION • Presence of a 4 -year period oscillation w on h off w off won

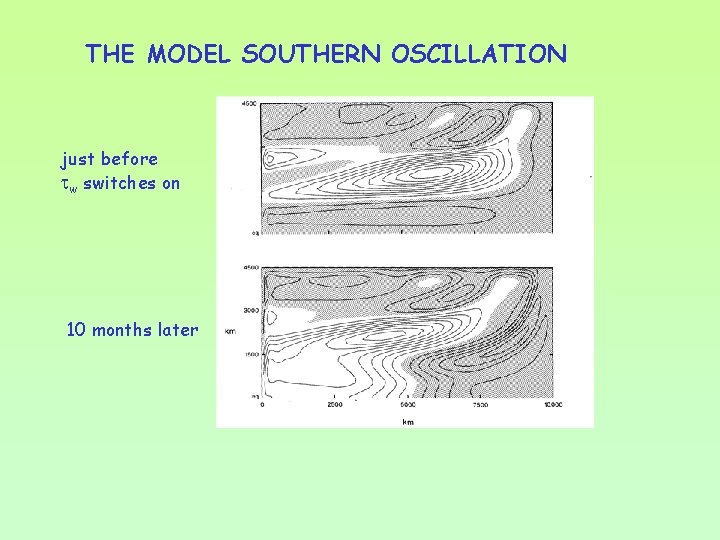
THE MODEL SOUTHERN OSCILLATION just before w switches on 10 months later

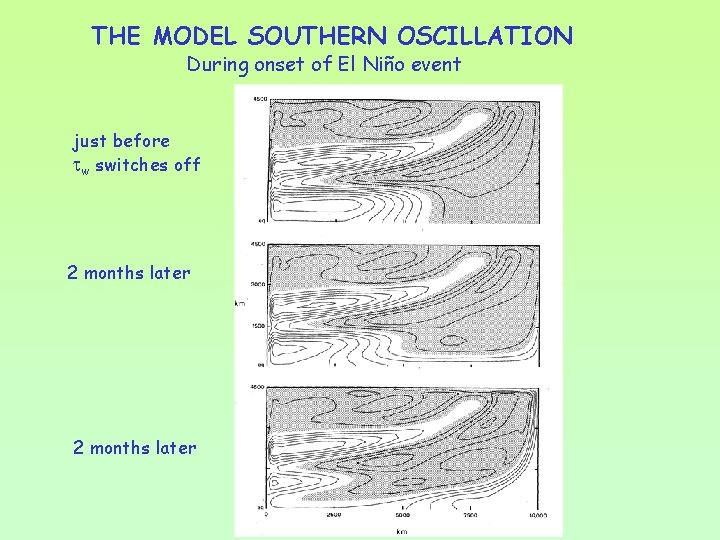
THE MODEL SOUTHERN OSCILLATION During onset of El Niño event just before w switches off 2 months later

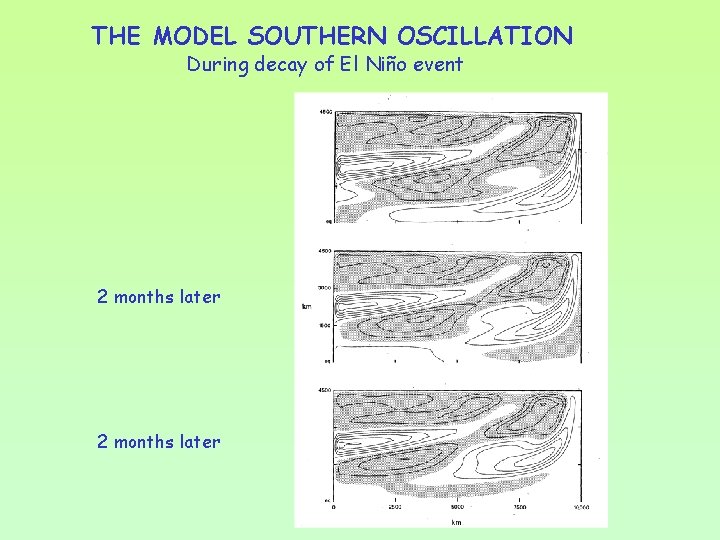
THE MODEL SOUTHERN OSCILLATION During decay of El Niño event 2 months later