A Model of Substructural State Matthew Fluet Cornell

A Model of Substructural State Matthew Fluet Cornell University Feb. 25, 2005

Introduction • Forms of “uniqueness” are appearing in programming languages Feb. 25, 2005 2

Introduction • Forms of “uniqueness” are appearing in programming languages • Cyclone – affine pointers, which may be discarded, but not duplicated • allow fine grained memory management • Vault – linear keys, which may be neither discarded nor duplicated • enforce resource management protocols Feb. 25, 2005 3

Introduction • Forms of “uniqueness” are appearing in programming languages • Cyclone – affine pointers, which may be discarded, but not duplicated • allow fine grained memory management • Vault – linear keys, which may be neither discarded nor duplicated • enforce resource management protocols • C / Java / SML – unrestricted objects that may be both discarded and duplicated Feb. 25, 2005 4

Introduction • But, programming with only unique objects is much too painful • Both Cyclone and Vault allow a programmer to put unique objects in shared objects • Impose a variety of restrictions to ensure that these mixed objects behave in a safe manner Feb. 25, 2005 5

Introduction • Natural to study a core language with mutable references of all flavors Feb. 25, 2005 6

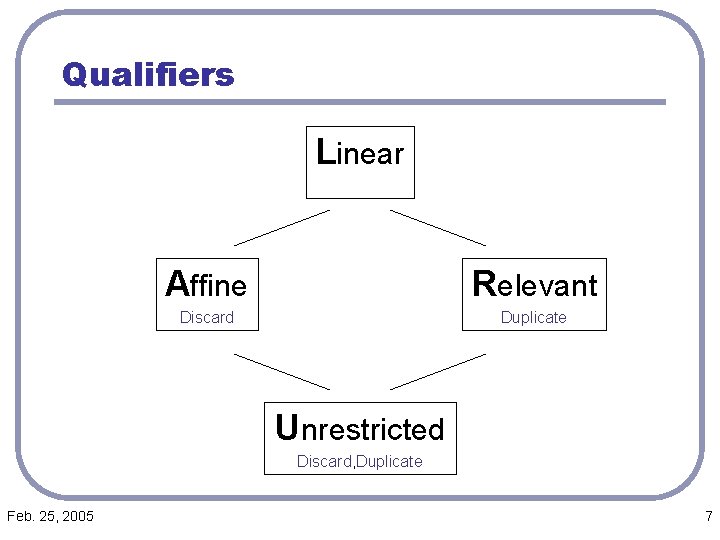
Qualifiers Linear Affine Relevant Discard Duplicate Unrestricted Discard, Duplicate Feb. 25, 2005 7

Qualifiers Unique objects – may be “used” at most once Linear Affine Relevant Discard Duplicate Unrestricted Discard, Duplicate Feb. 25, 2005 Shared objects – may be copied 8

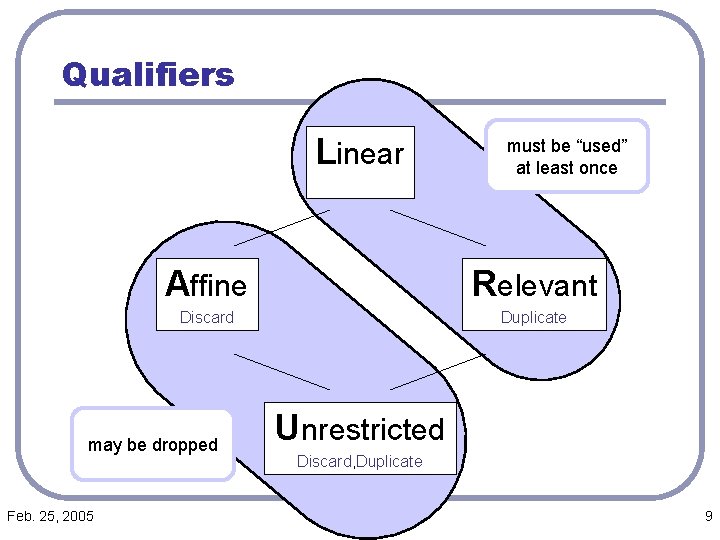
Qualifiers Linear Affine Relevant Discard Duplicate may be dropped Feb. 25, 2005 must be “used” at least once Unrestricted Discard, Duplicate 9

Introduction • Natural to study a core language with mutable references of all qualifiers • Raises design questions: • What does it mean to copy or drop a ref? • What operations make sense on different refs? • What combinations of qualifiers for a reference and its contents make sense? • Can one construct a reasonable model for such a language? Feb. 25, 2005 10

Outline • A Substructural Type System • … with References • Model Teaser Feb. 25, 2005 11

A Substructural Type System • Qualifiers q : : = U j R j A j L • Pre. Types t : : = 1 j t 1 t 2 j t 1 ( t 2 • Types t : : = qt Feb. 25, 2005 12

A Substructural Type System • Non-examples • U (A t 1 At 2), U(Rt 1 Rt 2), U(Lt 1 Lt 2) • Feb. 25, 2005 13

A Substructural Type System • Non-examples • • U (A t 1 At 2), U(Rt 1 Rt 2), U(Lt 1 Lt 2) copy hv 1, v 2 i ! hhv 1, v 2 i, hv 1, v 2 ii v 1 and v 2 may be used more than once Feb. 25, 2005 14

A Substructural Type System • Non-examples • • U (A t 1 At 2), U(Rt 1 Rt 2), U(Lt 1 Lt 2) copy hv 1, v 2 i ! hhv 1, v 2 i, hv 1, v 2 ii v 1 and v 2 may be used more than once Feb. 25, 2005 15

A Substructural Type System • Non-examples • • U (A t 1 At 2), U(Rt 1 Rt 2), U(Lt 1 Lt 2) copy hv 1, v 2 i ! hhv 1, v 2 i, hv 1, v 2 ii drop hv 1, v 2 i ! hi v 1 and v 2 may be used more than once v 1 and v 2 are not used Feb. 25, 2005 16

A Substructural Type System • Non-examples • • U (A t 1 At 2), U(Rt 1 Rt 2), U(Lt 1 Lt 2) copy hv 1, v 2 i ! hhv 1, v 2 i, hv 1, v 2 ii drop hv 1, v 2 i ! hi v 1 and v 2 may be used more than once v 1 and v 2 are not used Feb. 25, 2005 17

… with References • Pre. Types t : : = … j ref t Feb. 25, 2005 18

… with References • Examples? • Feb. 25, 2005 U(ref Ut), U(ref Rt), U(ref At), U(ref Lt) 19

… with References • Examples? • U(ref Ut), U(ref Rt), U(ref At), U(ref Lt) copy l ! hl, li l may be used more than once; but contents are not copied drop l ! hi l may is not used; and contents are dropped Feb. 25, 2005 20

… with References • Examples? • • U(ref Ut), U(ref Rt), U(ref At), U(ref Lt) copy l ! hl, li l may be used more than once; but contents are not copied drop l ! hi l may is not used; and contents are dropped Feb. 25, 2005 21

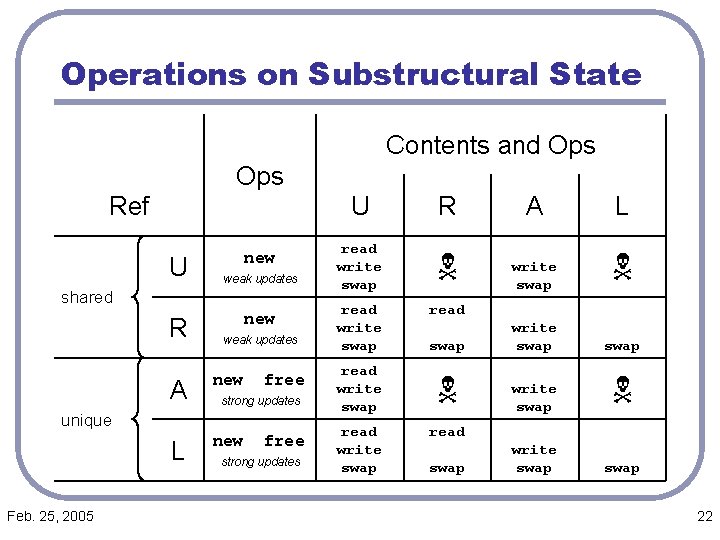
Operations on Substructural State Contents and Ops Ref U new weak updates shared R new weak updates A new L new free strong updates unique Feb. 25, 2005 free strong updates U R A L read write swap write swap read write swap read swap 22

A Model of Substructural State • Model a type as a set of tuples of qualifier, value, and local store typing «t¬ : : = { (q, y, v), …} • Model a local store typing as a partial map from locations to qualifiers and types y : : = { l a (q, «t¬), … } Feb. 25, 2005 23

A Model of Substructural State • Model a type as a set of tuples of qualifier, value, and local store type • Model a local store type as a partial map from locations to qualifiers and types • Local store of v only defined on those locations that appear as sub-expressions of v Feb. 25, 2005 24

A Model of Substructural State • Model a type as a set of tuples of qualifier, value, and local store type • Model a local store type as a partial map from locations to qualifiers and types • Local store of v only defined on those locations that appear as sub-expressions of v • Further restrictions to rule out stores Feb. 25, 2005 25

A Model of Substructural State • Why only a local store type? • Storing a unique object in a shared reference “hides” the unique object • Using the global store – difficult to identify the “real” occurrence of a unique location Feb. 25, 2005 26

A Model of Substructural State • How can we check that a global store satisfies a local store type? • Use a Garbage Collector Feb. 25, 2005 27

Store Satisfaction store s l 4 a v 4 l 7 a v 7 y l 1 a v 1 l 5 a v 5 l 8 a v 8 l 1 a t 1 l 2 a v 2 l 3 a v 3 Feb. 25, 2005 l 9 a v 9 l 6 a v 6 satisfies l 2 a t 2 l 3 a t 3 28

Store Satisfaction store s l 4 a v 4 l 7 a v 7 y l 1 a v 1 l 5 a v 5 l 8 a v 8 l 1 a t 1 l 2 a v 2 l 3 a v 3 l 9 a v 9 satisfies l 2 a t 2 l 3 a t 3 l 6 a v 6 These are the roots Feb. 25, 2005 29

Store Satisfaction store s l 4 a v 4 l 7 a v 7 y l 1 a v 1 l 5 a v 5 l 8 a v 8 l 1 a t 1 l 2 a v 2 l 3 a v 3 l 9 a v 9 satisfies l 2 a t 2 l 3 a t 3 l 6 a v 6 N if there exists a set of locations l 4 l 7 l 5 l 9 l 6 These are the non-roots Feb. 25, 2005 30

Store Satisfaction and local store types yl (l 2 dom(y) ] N) that merge These are the child locations traced from the contents of l Feb. 25, 2005 31

Store Satisfaction and local store types yl (l 2 dom(y) ] N) that merge Y* l 4 a t 4 l 1 a t 1 l 5 a t 5 l 2 a t 2 l 3 a t 3 l 7 a t 7 l 9 a t 9 ¯ l 2 dom(y) ] N yl l 6 a t 6 The global store type Feb. 25, 2005 =y¯ The local store types are compatible (non-contradictory) 32

Store Satisfaction and local store types yl (l 2 dom(y) ] N) that merge Y* l 4 a t 4 l 1 a t 1 l 5 a t 5 l 2 a t 2 l 3 a t 3 l 7 a t 7 l 9 a t 9 ¯ l 2 dom(y) ] N yl l 6 a t 6 The global store type Feb. 25, 2005 =y¯ Don’t trace a unique location more than once 33

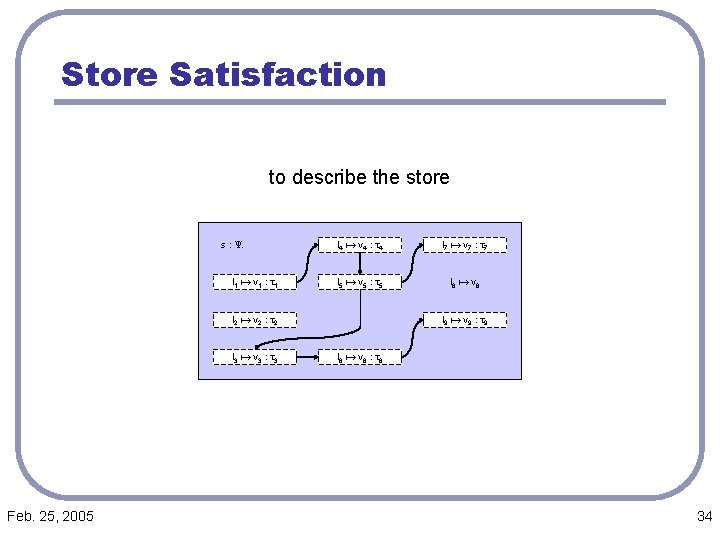
Store Satisfaction to describe the store s : Y* l 1 a v 1 : t 1 l 4 a v 4 : t 4 l 7 a v 7 : t 7 l 5 a v 5 : t 5 l 8 a v 8 l 2 a v 2 : t 2 l 3 a v 3 : t 3 Feb. 25, 2005 l 9 a v 9 : t 9 l 6 a v 6 : t 6 34

Conclusion and Future Work • Core language, type-system, and model • Model more advanced features • Cyclone – alias construct allows a unique pointer to be treated as shared for a limited scope • Vault – focus construct allows a shared object to be treated as unique for a limited scope Feb. 25, 2005 35

Feb. 25, 2005 36

Structural Lemmas • Exchange: • If G 1, x 1: t 1, x 2: t 2, G 2 ` e : t, then G 1, x 2: t 2, x 1: t 1, G 2 ` e : t. • Contraction: • If G 1, x 1: tx, x 2: tx, G 2 ` e : t, then G 1, x: tx, G 2 ` e[x/x 1][x/x 2] : t. • Weakening: • If G ` e : t, then G, x: tx ` e : t. Feb. 25, 2005 37

Structural Lemmas • Exchange: • If G 1, x 1: t 1, x 2: t 2, G 2 ` e : t, then G 1, x 2: t 2, x 1: t 1, G 2 ` e : t. • Contraction: Duplicate • If G 1, x 1: tx, x 2: tx, G 2 ` e : t, then G 1, x: tx, G 2 ` e[x/x 1][x/x 2] : t. • Weakening: Discard • If G ` e : t, then G, x: tx ` e : t. Feb. 25, 2005 38

Qualifiers Linear Exch Affine Relevant Exch, Weak Exch, Cntr Unrestricted Exch, Cntr, Weak Feb. 25, 2005 39

Structural Lemmas Revisited • Contraction: • If q ¹ R and G 1, x 1: qtx, x 2: qtx, G 2 ` e : t, then G 1, x 1: qtx, G 2 ` e[x/x 1][x/x 2] : t. • Weakening: • If q ¹ A and G ` e : t, then G, x: qtx ` e : t. Feb. 25, 2005 40

Operational Semantics s : : = {l 1 a v 1, …, ln a vn} (s, new v) ! (s ] {l a v}, l) (s ] {l a v}, free l) ! (s, v) (s ] {l a v}, rd l) ! (s ] {l a v}, hl, vi) (s ] {l a v 1}, wr l v 2) ! (s ] {l a v 2}, l) (s ] {l a v 1}, sw l v 2) ! (s ] {l a v 2}, hl, v 1 i) Feb. 25, 2005 41

A Model of Substructural State • Model a type as a set of tuples of qualifier, value, and local store type • Model a local store type as a partial map from locations to qualifiers and types Feb. 25, 2005 42

A Model of Substructural State • Model a type as a set of tuples Pre. Type = Ã(Qual £ Value £ Loc. Store) Type = Pre. Type • Model a local store type as a partial map Loc. Store = Locs ! (Qual £ Type)? • Cardinality problem is handled by stratifying definitions with “# of steps to run the program” Feb. 25, 2005 43

A Model of Substructural State Pre. Type = { c 2 Ã(Qual £ Value £ Loc. Store) j for all (q, v, y) 2 c, each location in y is mapped to a qualifier ¹ q } Type = { c 2 Pre. Type j all qualifiers in c are the same } Loc. Store = { y 2 Locs ! (Qual £ Type)? j each location is mapped to a type consistent with the location’s qualifier } Feb. 25, 2005 44