A microwavecavity parametric amplifier for studying the Dynamical

A microwave-cavity parametric amplifier for studying the Dynamical Casimir effect MIR experiment GR – Les Houches 2014 1

Summary Dynamical Casimir Effect with microwave cavities Parametric amplification: degenerate case Parametric amplification: 1) RF or 2) Laser Excitation Study of thermal background - time evolution of thermal distribution • Current status – perspectives/Conclusion • • GR – Les Houches 2014 2

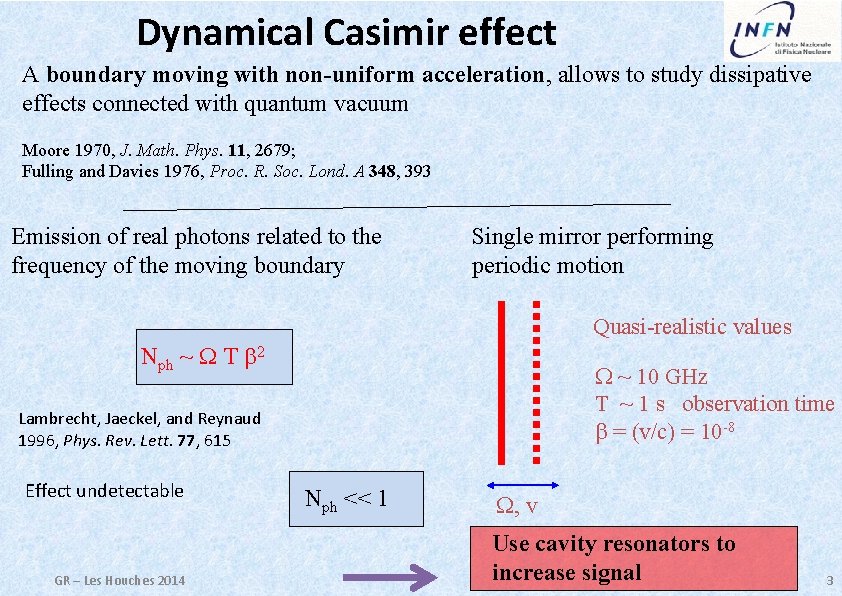
Dynamical Casimir effect A boundary moving with non-uniform acceleration, allows to study dissipative effects connected with quantum vacuum Moore 1970, J. Math. Phys. 11, 2679; Fulling and Davies 1976, Proc. R. Soc. Lond. A 348, 393 Emission of real photons related to the frequency of the moving boundary Single mirror performing periodic motion Quasi-realistic values Nph ~ W T b 2 W ~ 10 GHz T ~ 1 s observation time b = (v/c) = 10 -8 Lambrecht, Jaeckel, and Reynaud 1996, Phys. Rev. Lett. 77, 615 Effect undetectable GR – Les Houches 2014 Nph << 1 W, v Use cavity resonators to increase signal 3

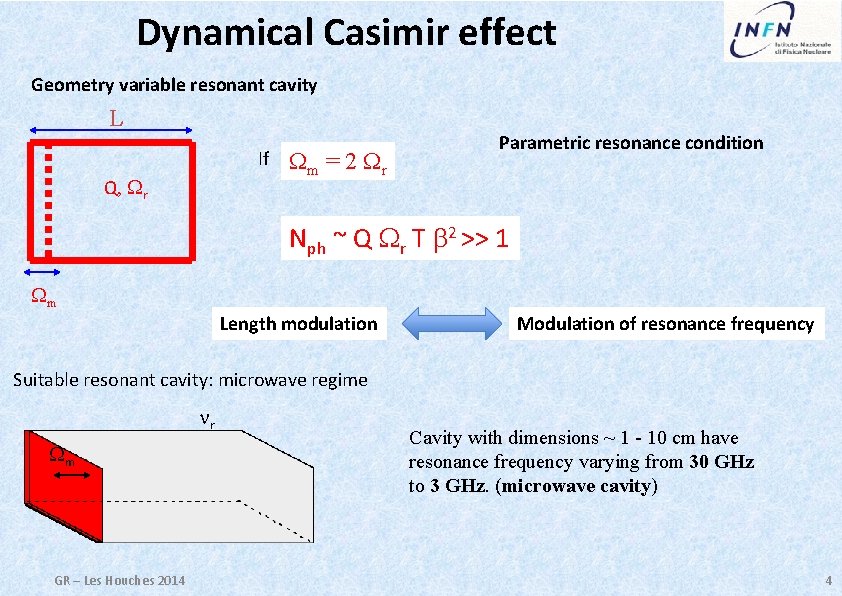
Dynamical Casimir effect Geometry variable resonant cavity L If Q, Wr Wm = 2 Wr Parametric resonance condition Nph ~ Q Wr T b 2 >> 1 Wm Length modulation Modulation of resonance frequency Suitable resonant cavity: microwave regime nr Wm GR – Les Houches 2014 Cavity with dimensions ~ 1 - 10 cm have resonance frequency varying from 30 GHz to 3 GHz. (microwave cavity) 4

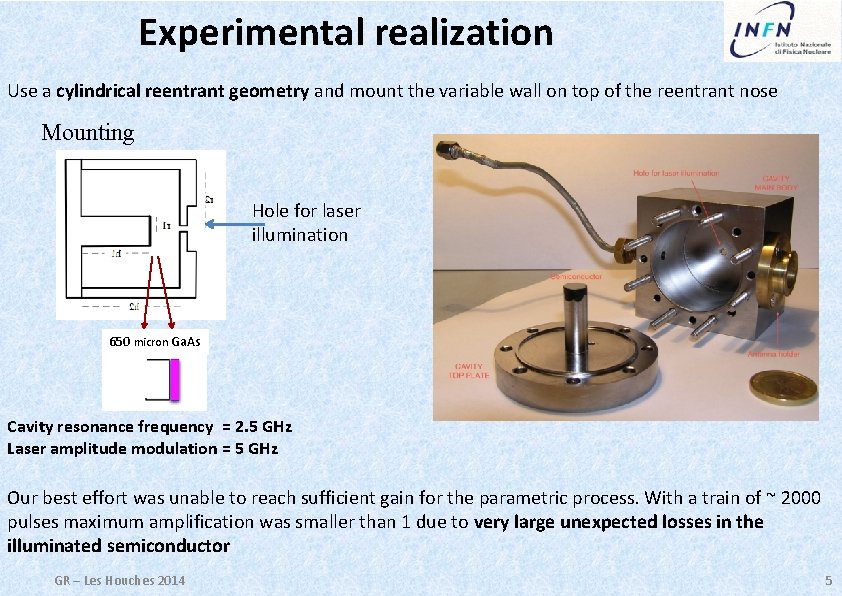
Experimental realization Use a cylindrical reentrant geometry and mount the variable wall on top of the reentrant nose Mounting Hole for laser illumination 650 micron Ga. As Cavity resonance frequency = 2. 5 GHz Laser amplitude modulation = 5 GHz Our best effort was unable to reach sufficient gain for the parametric process. With a train of ~ 2000 pulses maximum amplification was smaller than 1 due to very large unexpected losses in the illuminated semiconductor GR – Les Houches 2014 5

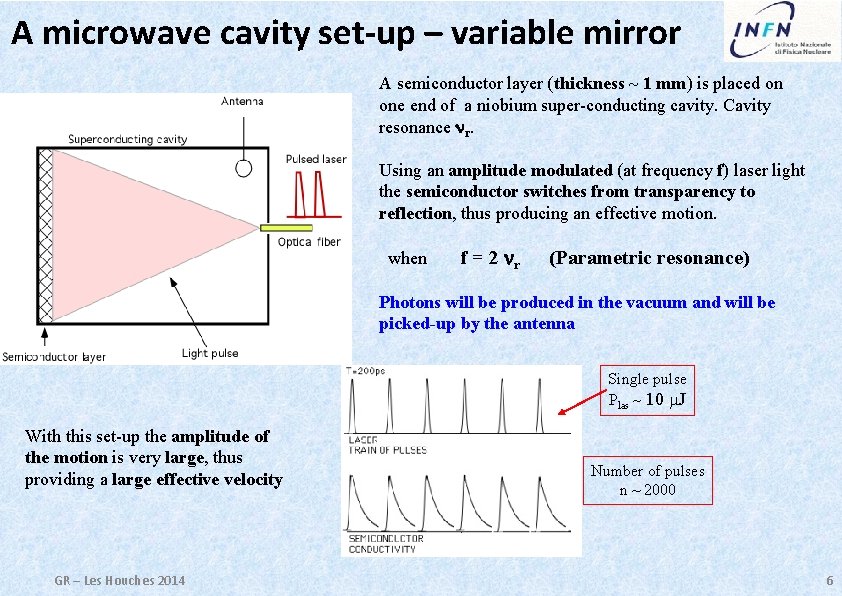
A microwave cavity set-up – variable mirror A semiconductor layer (thickness ~ 1 mm) is placed on one end of a niobium super-conducting cavity. Cavity resonance nr. Using an amplitude modulated (at frequency f) laser light the semiconductor switches from transparency to reflection, thus producing an effective motion. when f = 2 nr (Parametric resonance) Photons will be produced in the vacuum and will be picked-up by the antenna Single pulse Plas ~ 10 m. J With this set-up the amplitude of the motion is very large, thus providing a large effective velocity GR – Les Houches 2014 Number of pulses n ~ 2000 6

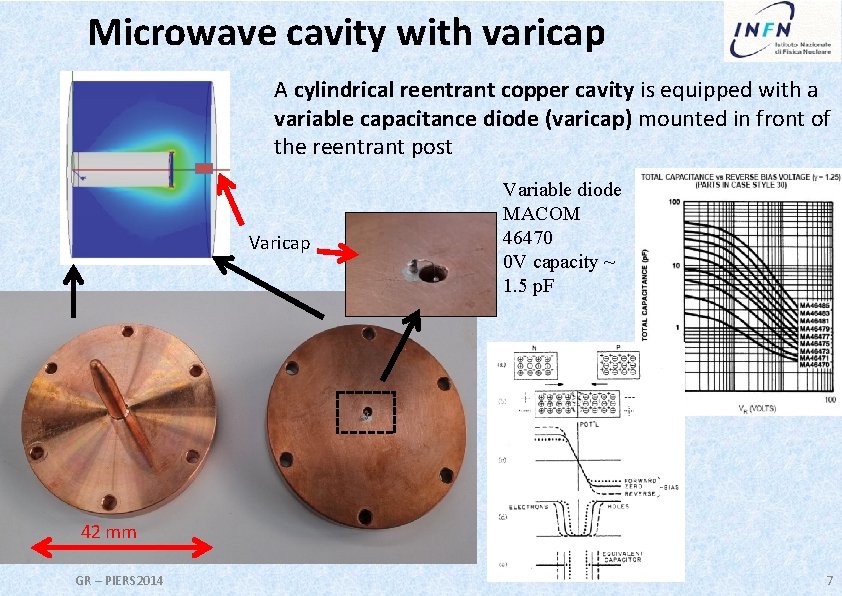
Microwave cavity with varicap A cylindrical reentrant copper cavity is equipped with a variable capacitance diode (varicap) mounted in front of the reentrant post Varicap Variable diode MACOM 46470 0 V capacity ~ 1. 5 p. F 42 mm GR – PIERS 2014 7

AC driving Let’s now suppose to modulate harmonically the resonance frequency, by using the varicap, at some frequency nvar. To study this process we model the microwave resonator with an LRC circuit with a variable capacitance in parallel Quality factor Resonance frequency Q=pncav/g ncav For t >0 Degenerate parametric amplifier: For f = 2 ncav the electromagnetic field in the resonant circuit, i. e. inside the microwave cavity, will exhibit an exponential growth of type exp(st), with s = p h ncav The effect is phase sensitive. j is the phase of the input field GR – Les Houches 2014 For t >> tp In case of dissipation 8

The way to the Dynamical Casimir effect To detect the DCE we have to realize an amplification of the vacuum, i. e. one has to work with an initial state having average thermal photon number smaller than 1. Moreover there must be no external contribution to the energy stored in the cavity. To realize this situation one has to check that the energy measured in the cavity corresponds to the average thermal photon bath energy for the corresponding thermodinamical temperature T. A reliable measurement of this is to determine the noise temperature of the parametric amplifier as a function of the cavity temperature: - Absolute determination of the parametric gain Variable resistor Variable input level (amplified noise source) GR – PIERS 2014 9

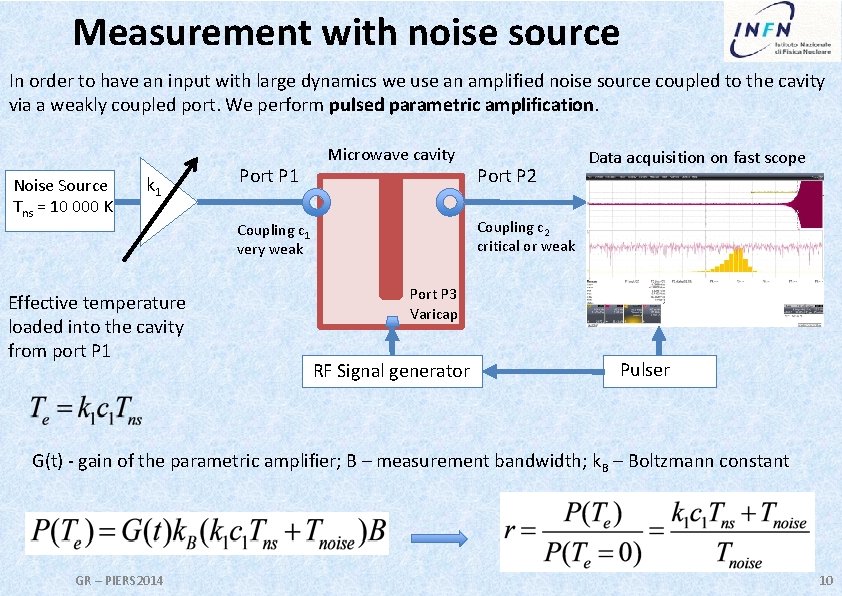
Measurement with noise source In order to have an input with large dynamics we use an amplified noise source coupled to the cavity via a weakly coupled port. We perform pulsed parametric amplification. Noise Source Tns = 10 000 K k 1 Effective temperature loaded into the cavity from port P 1 Port P 1 Microwave cavity Port P 2 Data acquisition on fast scope Coupling c 2 critical or weak Coupling c 1 very weak Port P 3 Varicap RF Signal generator Pulser G(t) - gain of the parametric amplifier; B – measurement bandwidth; k. B – Boltzmann constant GR – PIERS 2014 10

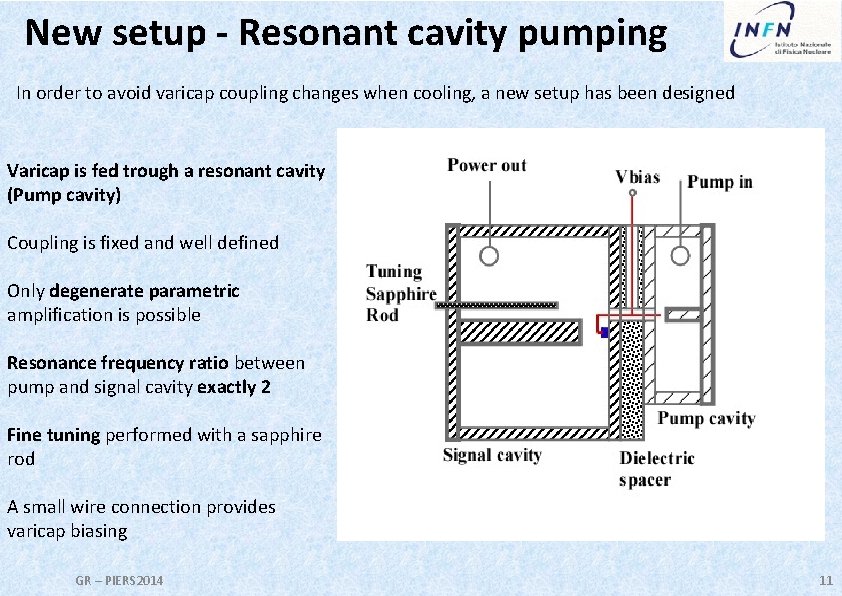
New setup - Resonant cavity pumping In order to avoid varicap coupling changes when cooling, a new setup has been designed Varicap is fed trough a resonant cavity (Pump cavity) Coupling is fixed and well defined Only degenerate parametric amplification is possible Resonance frequency ratio between pump and signal cavity exactly 2 Fine tuning performed with a sapphire rod A small wire connection provides varicap biasing GR – PIERS 2014 11

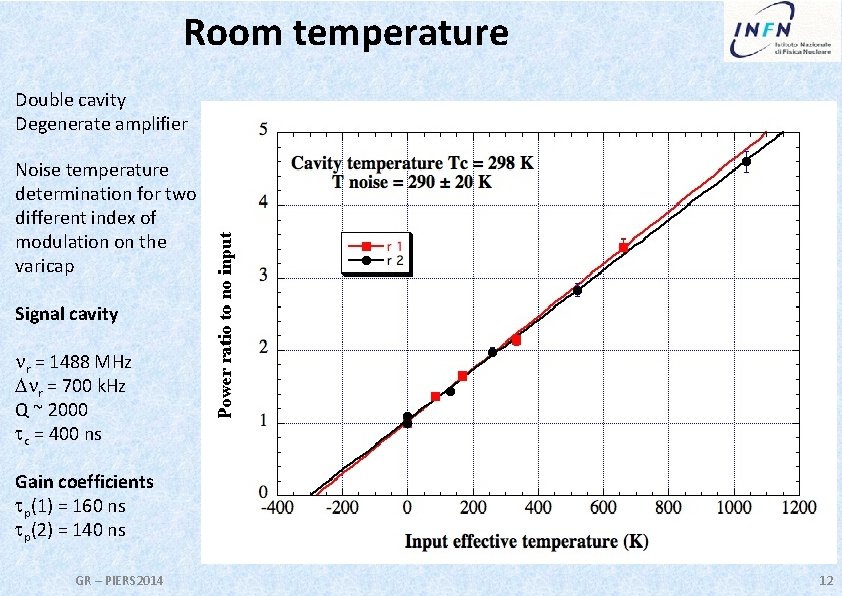
Room temperature Double cavity Degenerate amplifier Noise temperature determination for two different index of modulation on the varicap Signal cavity nr = 1488 MHz Dnr = 700 k. Hz Q ~ 2000 tc = 400 ns Gain coefficients tp(1) = 160 ns tp(2) = 140 ns GR – PIERS 2014 12

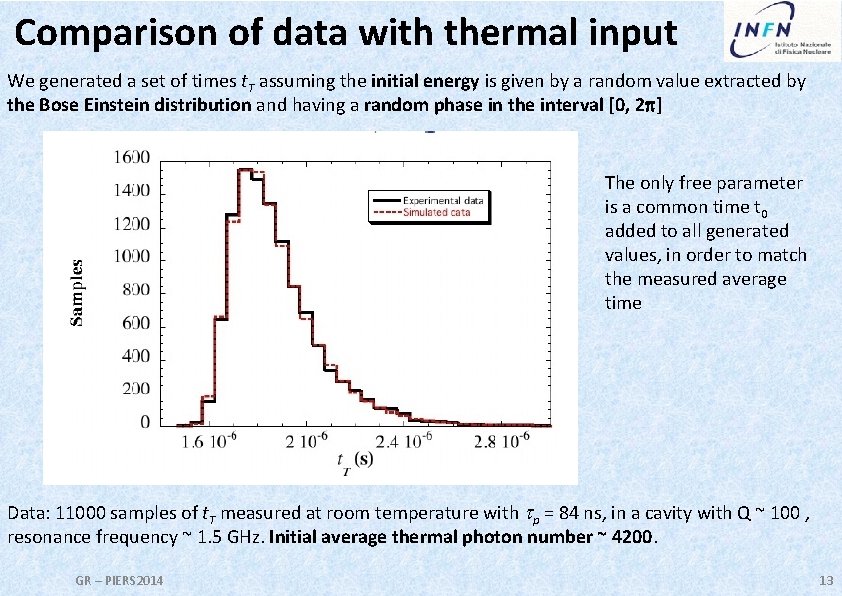
Comparison of data with thermal input We generated a set of times t. T assuming the initial energy is given by a random value extracted by the Bose Einstein distribution and having a random phase in the interval [0, 2 p] The only free parameter is a common time t 0 added to all generated values, in order to match the measured average time Data: 11000 samples of t. T measured at room temperature with tp = 84 ns, in a cavity with Q ~ 100 , resonance frequency ~ 1. 5 GHz. Initial average thermal photon number ~ 4200. GR – PIERS 2014 13

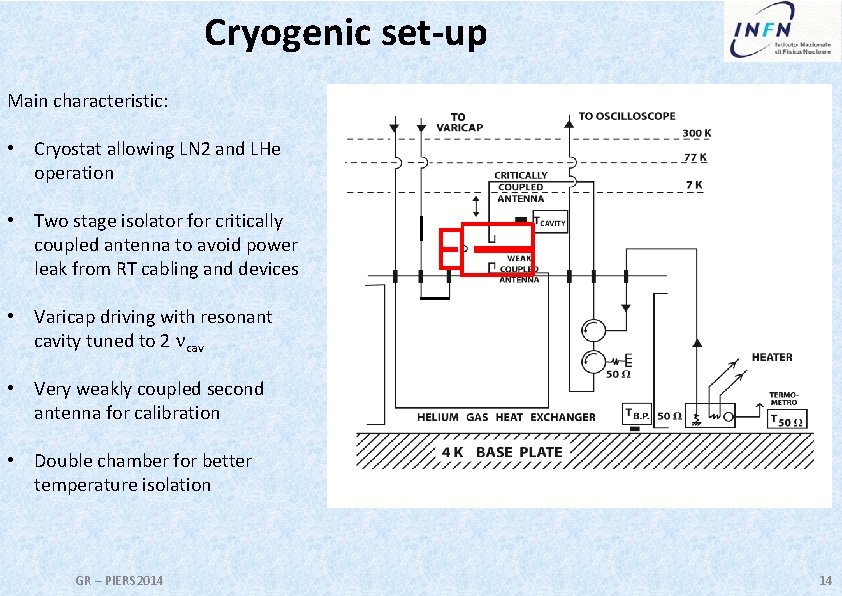
Cryogenic set-up Main characteristic: • Cryostat allowing LN 2 and LHe operation • Two stage isolator for critically coupled antenna to avoid power leak from RT cabling and devices • Varicap driving with resonant cavity tuned to 2 ncav • Very weakly coupled second antenna for calibration • Double chamber for better temperature isolation GR – PIERS 2014 14

The current experimental apparatus The cavities with antennas and varicap biasing Varicap biasing Signal cavity Antennas GR – PIERS 2014 Pump cavity Thermal and electromagnetic isolation stages and filtering 15

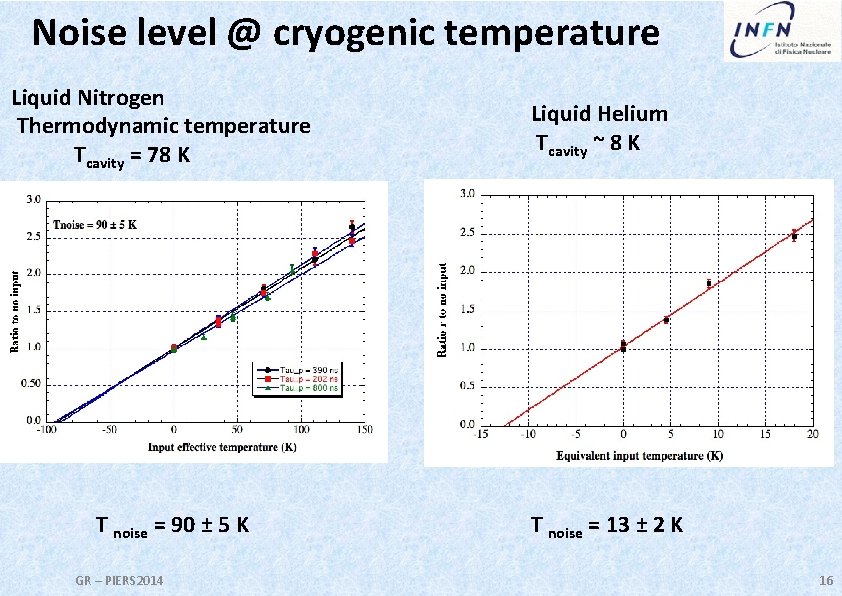
Noise level @ cryogenic temperature Liquid Nitrogen Thermodynamic temperature Tcavity = 78 K T noise = 90 ± 5 K GR – PIERS 2014 Liquid Helium Tcavity ~ 8 K T noise = 13 ± 2 K 16

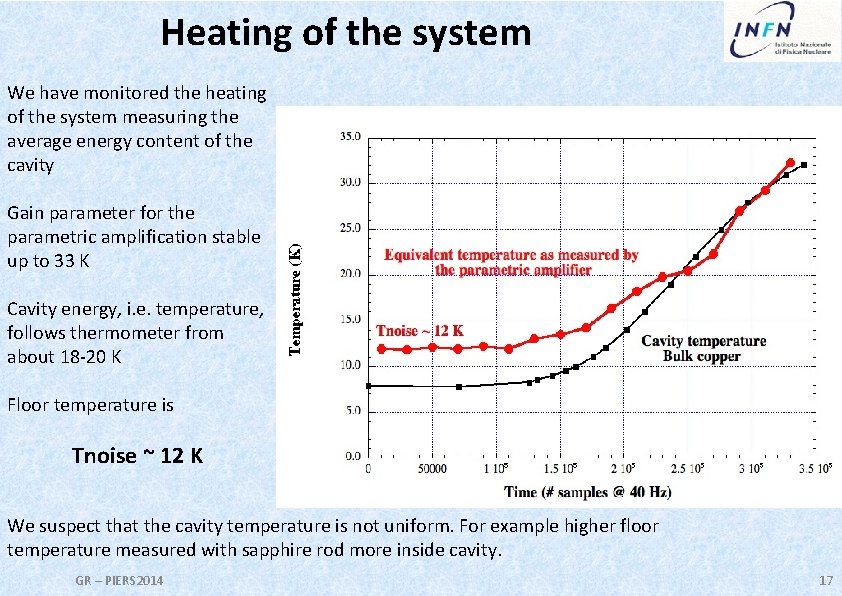
Heating of the system We have monitored the heating of the system measuring the average energy content of the cavity Gain parameter for the parametric amplification stable up to 33 K Cavity energy, i. e. temperature, follows thermometer from about 18 -20 K Floor temperature is Tnoise ~ 12 K We suspect that the cavity temperature is not uniform. For example higher floor temperature measured with sapphire rod more inside cavity. GR – PIERS 2014 17

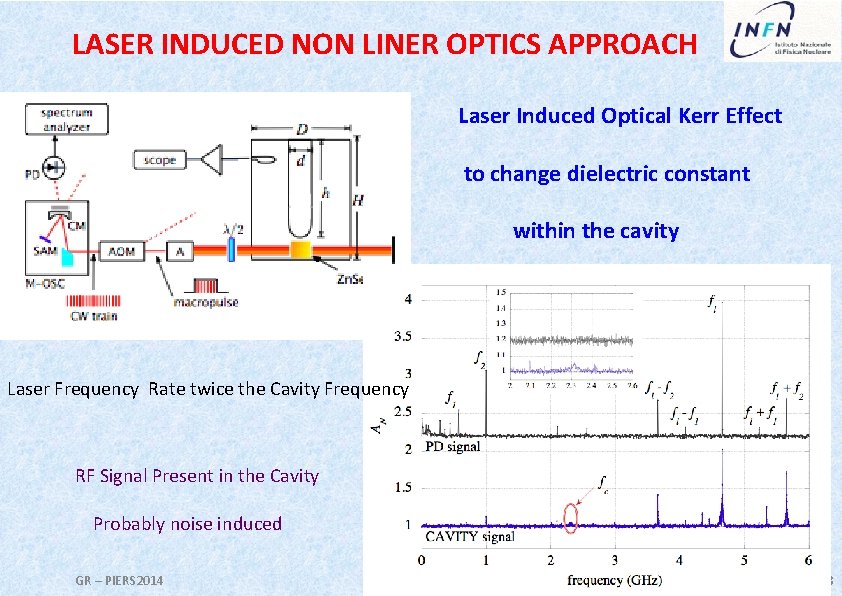
LASER INDUCED NON LINER OPTICS APPROACH Laser Induced Optical Kerr Effect to change dielectric constant within the cavity Laser Frequency Rate twice the Cavity Frequency RF Signal Present in the Cavity Probably noise induced GR – PIERS 2014 18

GR – PIERS 2014 19

Conclusioni • Parametric amplification Work at 8 -10 Kelvin • At 10 Kelvin @ 1, 5 GHz ( 10 -5 e. V ) N fotoni medio =100 Energia E. M. Misurata = 10 -3 e. V Nuovo set up Criogenico @ Kelvin Richiesta 7 Keuro Sotto Dotazione GR – PIERS 2014 20

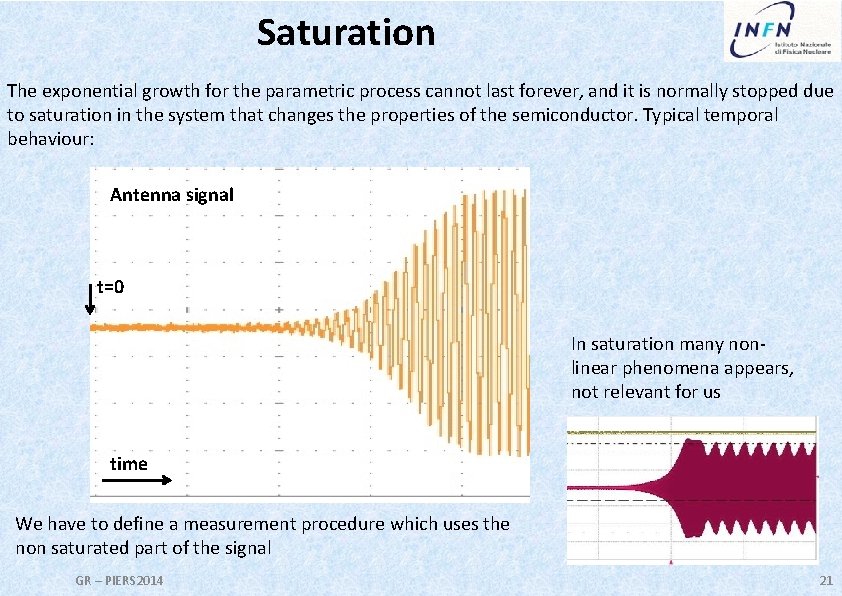
Saturation The exponential growth for the parametric process cannot last forever, and it is normally stopped due to saturation in the system that changes the properties of the semiconductor. Typical temporal behaviour: Antenna signal t=0 In saturation many nonlinear phenomena appears, not relevant for us time We have to define a measurement procedure which uses the non saturated part of the signal GR – PIERS 2014 21

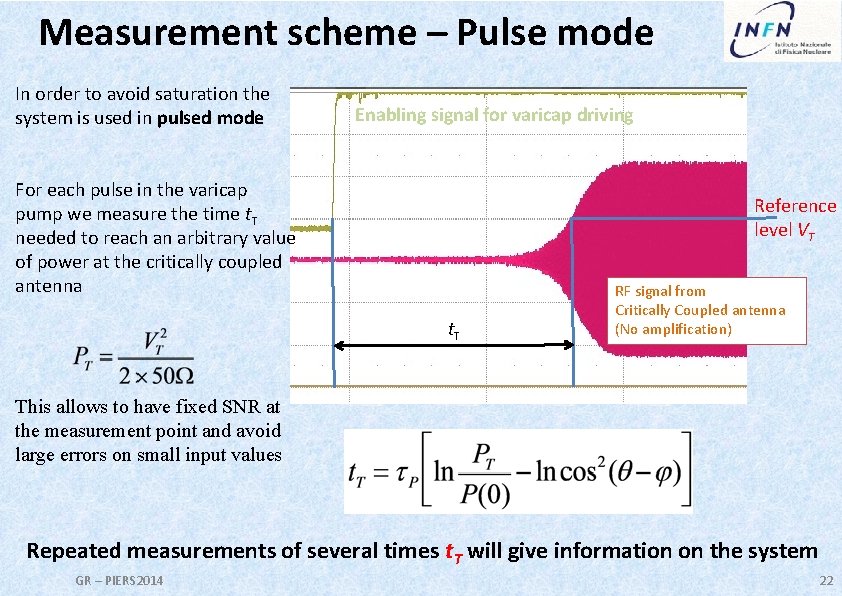
Measurement scheme – Pulse mode In order to avoid saturation the system is used in pulsed mode Enabling signal for varicap driving For each pulse in the varicap pump we measure the time t. T needed to reach an arbitrary value of power at the critically coupled antenna Reference level VT t. T RF signal from Critically Coupled antenna (No amplification) This allows to have fixed SNR at the measurement point and avoid large errors on small input values Repeated measurements of several times t. T will give information on the system GR – PIERS 2014 22