A Methodology for Producing Identical Double Precision FloatingPoint

A Methodology for Producing Identical Double Precision Floating-Point Results Frederick (Eric) Mc. Intosh (Honorary Group Member AB/ABP CERN) eric. mcintosh@cern. ch

A Quote “Guaranteeing that two runs of a program will produce exactly the same results is extremely difficult and may be impossible in practice. ” From “Numerical Replications of Computer Simulations: Some Pitfalls and How To Avoid Them” Theodore C. Belding (January, 2000)

Obligatory Reading “What Every Computer Scientist Should Know About Floating-Point Arithmetic” David Goldberg March, 1991 “Most programs will actually produce different results on different systems” “Why do we need a floating-point arithmetic standard? ” Prof. W. Kahan, Berkeley, 1981 3

Why Differences? • Binary floating-point arithmetic is inexact and rounding “error” accumulates and analysis is impractical/impossible • Mathematically equivalent expressions will often give different results e. g. (a*b)/c != a*(b/c) • Results depend on the order of evaluation of an expression –may have catastrophic cancellation • Hardware today “always” conforms to IEEE 754 but the standard has loopholes and is incomplete • Software standards are evolving but are incomplete with respect to floating-point 4

IEEE 754 (rev 2008) • Defines unique reproducible result for +, -, *, /, and sqrt – the correctly rounded result being the floating-point number closest to the exact result • It is incomplete and open to interpretation • Needs to be combined with the language standard • Strict compliance conflicts with performance • Does NOT cover Elementary Functions 5

…. . more • • • 4 rounding modes (up, down, nearest, -> 0) We consider only “round to nearest” _rn Double Precision ~15 (and a bit) decimal digits Range from ~-10**308 to 10**308 but also Na. Ns and +/- Infinity • Covers gradual underflow and exceptions • ULP is Unit in the Last (binary) Place the smallest representable difference between two numbers

Floating-Point Arithmetic • - Sign, Exponent, Mantissa ( bits) • Single Precision (SP) – 1, 8, 23 (32) • Double Precision (DP) – 1, 11, 52 (64) • Extended Precision (EP) A mongrel? – 1, 15, 64 (80) • Quadruple Precision – 1, 15, 112 (128) • Arbitrary Precision (Maple, MPFR, etc) 7

Programming Standards • • (CERN) FORTRAN 66 Fortran 77, 90, 95, 2003 C/C++ C 99 Fortran 2003 (when available) and C 99 represent an immense step forward • BUT benefits are often long-term and the extra time required to conform is NOT appreciated by management and seen as a burden by the programmer 8

Case Study (Six. Track) • Used to study LHC Beam Dynamics and determine the Dynamic Aperture with and without weak-strong beam effects • Around 60, 000 lines of Fortran 77 (almost) code ported from IBM to Cray, Dec, and to PCs and part of SPECfp 2000 ($3000. - for CERN!) • It is a DIVERGENT application in that even a 1 ULP difference will grow exponentially with time giving significantly different results at the onset of chaotic motion (c. f. Non-linear, Lorentz, “butterfly” effect) • Particle motion is deterministic but there is no theory for predicting the onset of chaotic motion 9

Six. Track (continued) • A typical LHC Study might require running from 10 to 100, 000 cases/jobs using 60 particles, one or more tunes, 10 initial amplitudes and 5 or more initial angles in phase space and a set of magnet errors for one million turns • Even on a modern PC this takes of the order of 10 hours for each case • Until now studies were limited by the available computer capacity 10

My Idea (not original) • Use ~10000 Windows desktops at CERN to run Six. Track (Play. Stations!) the so called CERN Physics Screen Saver (CPSS) project • At least double the tracking capacity and potentially provide an order of magnitude increase for zero financial investment • Later switched to BOINC (the Berkeley Open Infrastructure for Network Computing) • This required the ability to verify results from almost any kind of PC (later MAC) running the various Operating Systems (Linux all brands, Windows all brands) • BOINC provides “Homogeneity” and “Epsilon” or “Own Brand” result verification 11

The Methodology Copyright F. Mc. Intosh and CERN • • • Restricted to double precision 64 bits, 32 -bit executables and ignores precise exception handling and underflow (for GPUs and SSE 2/SSE 3) It should apply equally to C (C++) C 99 standard compliant programs but more easily applicable Requires source code availability (no libraries) Will reduce performance Produces identical (0 ULP difference) results on the three principal Operating Systems and levels, using any of four different Fortran compilers at “any” optimisation level 12

Methodology 1) Fortran 77 add parentheses to ensure unique order of expression evaluation 2) Disable Extended Precision as required by 3) and 4) anyway. Not available for SSE 2/SSE 3 3) Use crlibm from ENS Lyon for the elementary functions (plus arcsine, arccosine and arctan 2) 4) Use David M. Gay routines formatted input (and output) available since 1990 5. Implement exponentiation a**b as exp(b*log(a)) NINT 6. Verify no difference between compile time and execute time evaluation of constants 7. Disable Fused Multiply Add (FMA) 8. (Persuade library providers to provide a portable version, using this methodology) 13

LHC@home • After applying the methodology to Sixtrack the BOINC project LHC@home is providing the equivalent computing power of some 25, 000 PCs (100, 000 processors, available 50% of the time, every case run twice). Unprecedented capacity for ABP. • No $25, 000 to buy them, no software licences, no cooling or power to pay • Undetected error rate is around 1 in 10, 000 (down from one in a hundred thousand one in a million ). 14

What next? • • • Fix error rate (LHC service is a priority). Publish for peer review (Berkeley and Lyon) Extend to 64 -bit executables C/C++ The GRID and the CLOUD Other application(s) at CERN such as Geant or an Experiment or Theory Applications such as Climate Prediction NASA, Molecular Dynamics, NAG library and Compiler Computer Games ARM processors, Tablets, Smart Phones and Raspberry Pi ($35. -, 800 MHz, 512 MB) WARNING: this application heavily uses CPU and device components. If you observe too high device temperature, 15 please stop computing or decrease CPU usage.

16

Acknowledgements • • • ABP Group for hosting me for 7 years and providing a couple of PCs and a software licence. BTE Desktop Support. M. Giovannozzi and F. Schmidt the Six. Track author for long time help and support and to R. De Maria and L. Deniau. EPFL and Prof. Rifkin and I. Zacharov for BOINC support ENS Lyon and F. Denichin for crlibm H. Renshall (IT/CERN retired) for the parentheses G. Erskine (CERN deceased) for outstanding help on numerical analysis and the Error Function of a Complex Number A. Wagner (CERN) for CPSS and B. Segal (CERN retired) for suggesting BOINC J. Boothroyd, formerly English Electric, for introducing me to Floating-Point Error Analysis (50 years ago) Prof. Kahan Berkeley for his work on IEEE 754 and his many publications Prof. Anderson Berkeley for BOINC and (last but not least) • The BOINC volunteers, 60, 000 worldwide for LHC@home 17

English Electric Deuce Computer 1960

Mercury Delay Lines

22

Computing at CERN • Dominated by the needs of the experiments • Accelerator design, a small fraction of the various mainframes (1964 – 1998) and the “PARC” IBM workstation cluster • In 1997 the LHC Machine Advisory Committee recommended more tracking • The “Numerical Accelerator Project”, NAP 23

Why Standards? • Should be evident: safety, quality, convenience for example, and they apply in all walks of life including computing • Program portability ensures fair competition for hardware and software acquisition • No monopolies (c. f. a giant corporation) • Should NOT be sacrificed to performance 24

Some simple test results • ULP – One Unit in the Last Place of the mantissa of a floating-point number (one part in roughly 10**16) – – – libm/crlibm IA 32: 304 differences of 1 ULP ibm IA 32/IA 64: 5 differences of 1 ULP libm IA 32/AMD 64: 7 differences of 1 ULP libm IA 64/AMD 64: 2 differences of 1 ULP libm/libm NO EP: 134623 differences of 1 ULP • NO differences with exp_rn • 1, 000 exp calls with random arguments (0, 1) 25

…and with lf 95 – lahey/crlibm IA 32: 134645 differences of 1 ULP – lahey IA 32/IA 64: 7 differences of 1 ULP – lahey IA 32/AMD 64: 7 differences of 1 ULP – lahey IA 64/AMD 64: 4 differences of 1 ULP • NO differences with exp_rn 26

When quadruple precision is not enough – The Table Maker’s Dilemma • Rounding the approximation of f(x) is not always the same as rounding f(x) • Worst case for exp(x), x=7. 5417527749959590085206221 e-10 • Binary example x=1. (52)1 *2 -53 exp(x)=1. (52)0 1 (104)1 010101… • quad (112 bit) approximations : 1. (51)0 1 (60)0 and 1. (51)0 0 (60)1 are both within 1 Quad ULP but which rounded value is nearest? 27

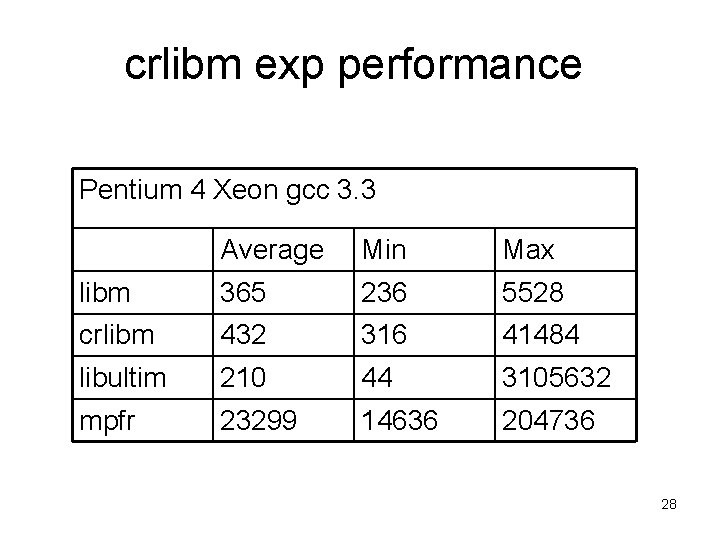
crlibm exp performance Pentium 4 Xeon gcc 3. 3 Average Min Max libm 365 236 5528 crlibm 432 316 41484 libultim 210 44 3105632 mpfr 23299 14636 204736 28