A Matrix Free Newton Krylov Method For Coupling

A Matrix Free Newton /Krylov Method For Coupling Complex Multi-Physics Subsystems Yunlin Xu School of Nuclear Engineering Purdue University October 23, 2006

Content ¨ Introduction ¨ MFNK and Optimal Perturbation Size Fixed Point Iteration (FPI) for coupling subsystems – – A Matrix Free Newton/Krylov method based on FPI Local Convergence analysis of MFNK Truncation and Round-off Error Estimation of Optimal Finite Difference Perturbation ¨ Global Convergence strategies – Line search – Model trust region ¨ Numerical Examples ¨ Summary

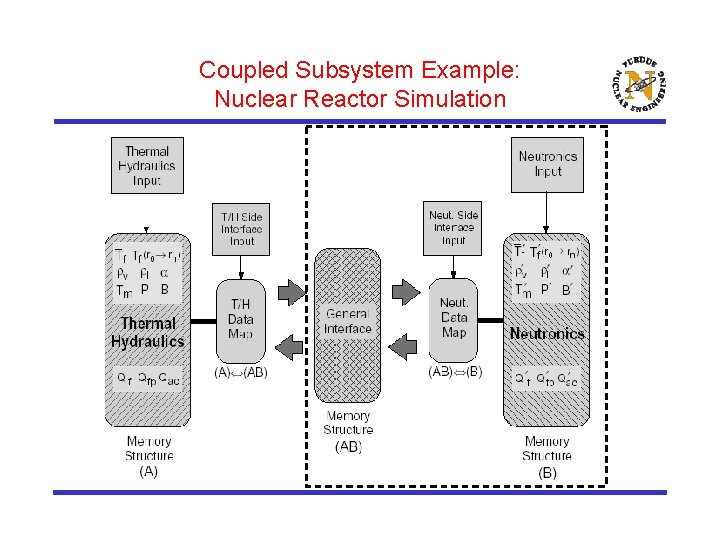
Features of Multi-Physics Subsystems ¨ Multiple nonlinear subsystems are coupled together: The solution of each subsystem depends on some external variables which come from the other system : internal variables : external variables ¨ Each subsystem can be solved with reliable methods as long as they remain decoupled

Two General Approaches for Coupling Subsystems ¨ Analytic Approach: reformulate the coupled system into a larger system of equations – Standard Newton-type methods can be applied ¨ Synthetic Approach: combine the subsystem solvers for the coupled system – utilize the well-tested and reliable solutions of each of the subsystems because: • It may be too expensive to reformulate the coupled system and forego the significant investment in developing reliable solvers for each of the subsystems. • One of the subsystems may be solved using commercial software that prevents access to the source code which makes it impossible to reformulate the coupled equations for the analytic approach

Coupled Subsystem Example: Nuclear Reactor Simulation

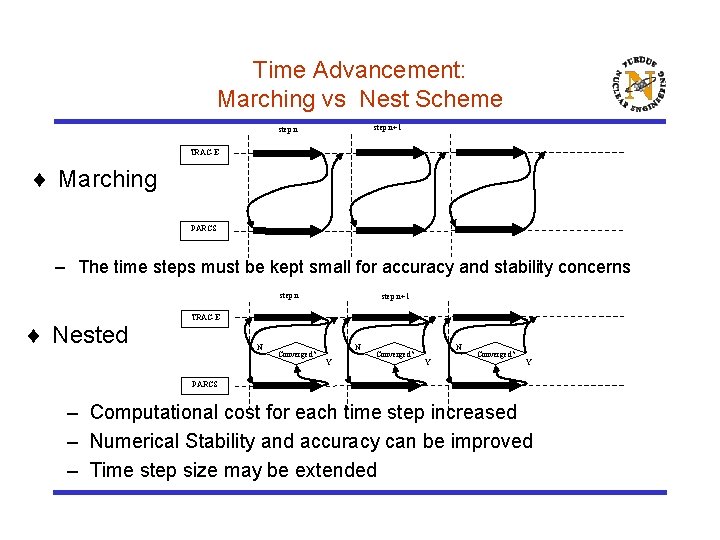
Time Advancement: Marching vs Nest Scheme step n+1 step n TRAC-E ¨ Marching PARCS – The time steps must be kept small for accuracy and stability concerns step n ¨ Nested step n+1 TRAC-E N Converged? N Y Converged? Y PARCS – Computational cost for each time step increased – Numerical Stability and accuracy can be improved – Time step size may be extended

Ringhals BWR Stability ¨ 48 hours on 2 GHz machine for initialization! 128 Chans 7

Synthetic Approaches ¨ Nested Iteration – Subsystems are chained in block Gauss-Seidel or block Jacobi iteration – Convergence is not guaranteed. ¨ Matrix Free Newton/Krylov Method – Approximate Mat-Vec by quotient: – The system Jacobian is not constructed – Local Convergence guaranteed ¨ Problems with Direct Application of MFNK for Coupling of Subsystems – Solvers for the subsystems are not fully utilized – Difficult to find a good preconditioner for MFNK – In some cases, it is not possible to obtain residuals for a subsystem if the solver of subsystem is commercial software which can be used only as a “black box”.

Objectives of Research ¨ Propose a general approach to implement efficient matrix free Newton/Krylov methods for coupling complex subsystems with their respective solvers ¨ Identify and address specific issues which arise in implementing MFNK for practical applications – Local convergence analysis of the matrix free Newton/Krylov method – Optimal perturbation size for the finite difference approximation in MFNK – Globally convergent strategies

Fixed Point Iteration for Coupling Subsystems ¨ Block Iteration for coupling subsystems are fixed point iterations ¨ The condition for convergence of FPI is ||Φ (x*)||<1. ¨ If ||Φ (x*)||>1, then the FPI may diverge 10

Matrix Free Newton Krylov Method Based on a Fixed Point iteration ¨ Define a nonlinear system: F(x)= Φ(x) -x =0 ¨ The solution of this system is the fixed point of function Φ(x), which is also the solution of original coupled nonlinear system ¨ MFNK algorithm: 11

Local Convergence of INM ¨ Inexact Newton Method (INM) ¨ Local Convergence of INM ¨ The convergence of INM depends on the inner residual, assume – If p 2, the INM has local q-quadratic convergence. – If 1<p<2, INM converges with q-order at least p. – If p=1 and , the INM has local q-linear convergence. 12

Local Convergence of MFNK ¨ MFNK is an INM The inner residual consists with: – iterative residual – finite difference residual ¨ There are two conflicting sources of error in finite difference: – Truncation error – Round off error 13

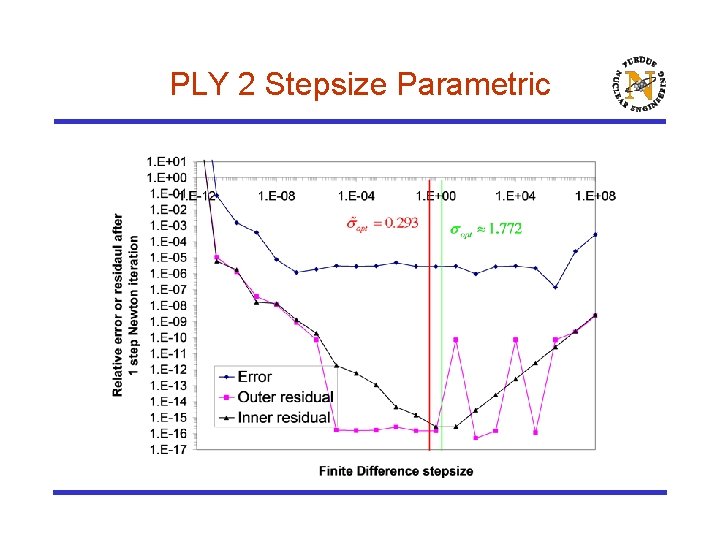
Local Convergence of MFNK (cont. ) ¨ The optimal should balance the round-off error and truncation error ¨ In theory, MFNK has local q-linear convergence, if ¨ In practice, MFNK can achieve q-quadratic convergence, if

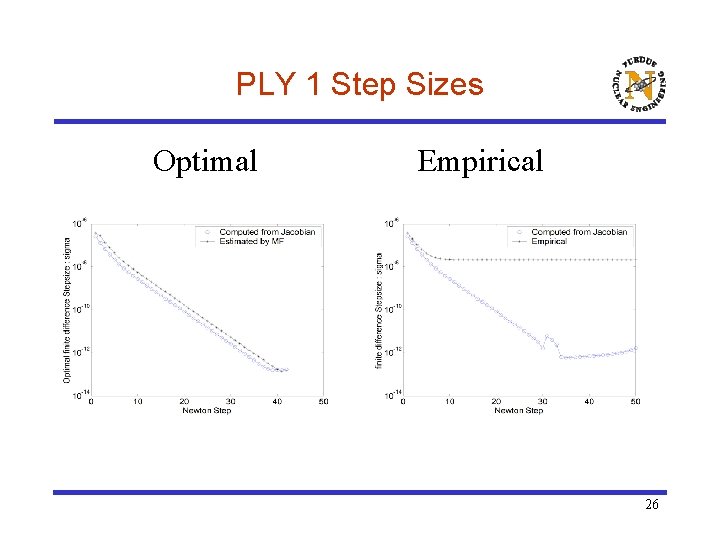
Optimal vs Empirical Perturbation Size ¨ The norm of the Jacobian and can be estimated with information provided by the MFNK algorithm: or ¨ An empirical prescription was proposed attempt to balance the truncation and round-off errors (Dennis) 15

Global Convergence Strategies ¨ Solution x* of system of nonlinear equation: F(x)=0 also the global minimizer of optimization problem: is ¨ Newton step s. N is the step from current solution to global minimizer of model problem: ¨ f(xc+s. N) may be larger than f(xc), due to big step s. N such that m(xc+s. N) is no longer a good approximation of f(xc+s. N). In this case, we need globally convergent strategy to force f(xc+s. N)<f(xc)

Descent Direction ¨ Newton step is descent direction of both objective function and its model: ¨ For any descent direction pk, there exist λ satisfies: (1) α-condition β-condition ¨ A sequence {xk} generated by xk+1=xk+λkpk satisfying previous condition will converge to a minimizer of f(x). (2) (1), (2) proofs can be found in Dennis & Schnabel’s book

Line Search ¨ Take MF Newton step as descent direction, and select λ to minimize a model of following function ¨ Quadratic model ¨ λ predicted from quadratic model

Information Required in Quadratic Model ¨ Two function values: ¨ One Gradient ¨ Approximations for Gradient in MFNK or 19

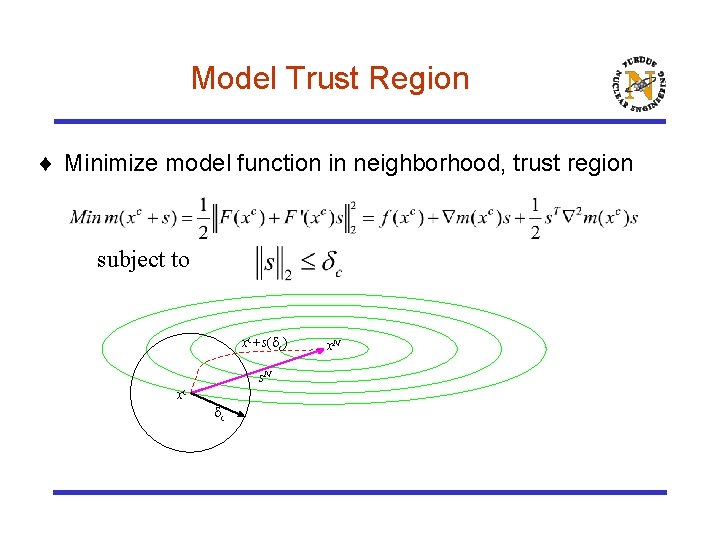
Model Trust Region ¨ Minimize model function in neighborhood, trust region subject to xc+s( c) s. N xc c x. N

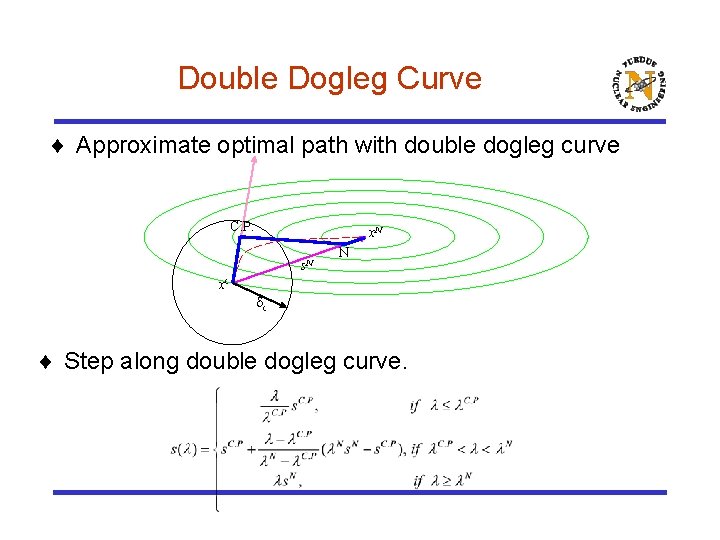
Double Dogleg Curve ¨ Approximate optimal path with double dogleg curve C. P. x. N s. N N xc c ¨ Step along double dogleg curve.

Cauchy Point ¨ Cauchy Point is minimizer in steepest descent direction ¨ Projection of Step for Cauchy Point on Krylov subspace (Brown & Saad)

Example Problem I: Polynomials ¨ Two dimensional second order polynomials ¨ Solution ¨ Jacobian ¨ Nonlinear level

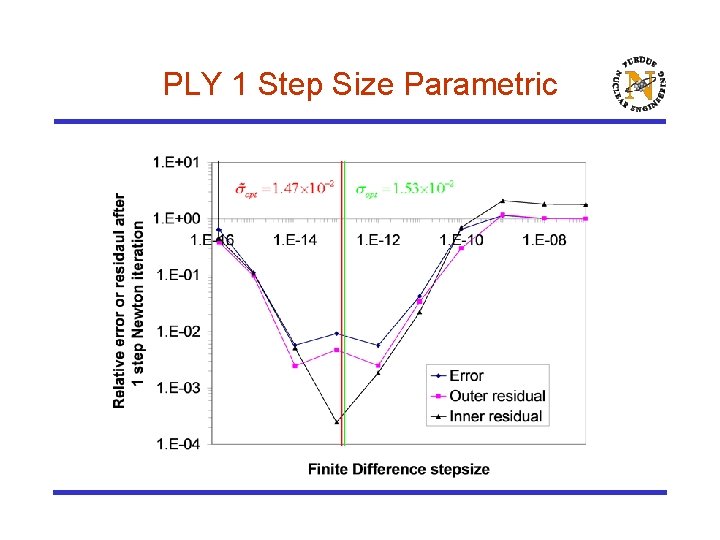
PLY 1 Truncation Error Dominated Case 24

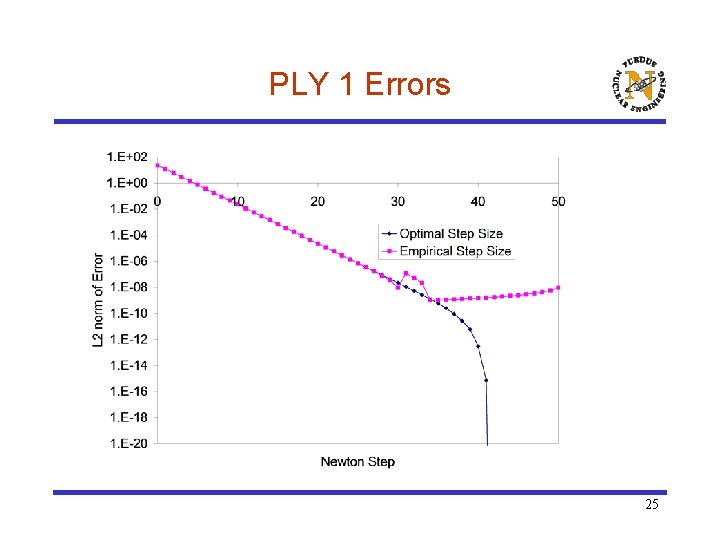
PLY 1 Errors 25

PLY 1 Step Sizes Optimal Empirical 26

PLY 1 Step Size Parametric

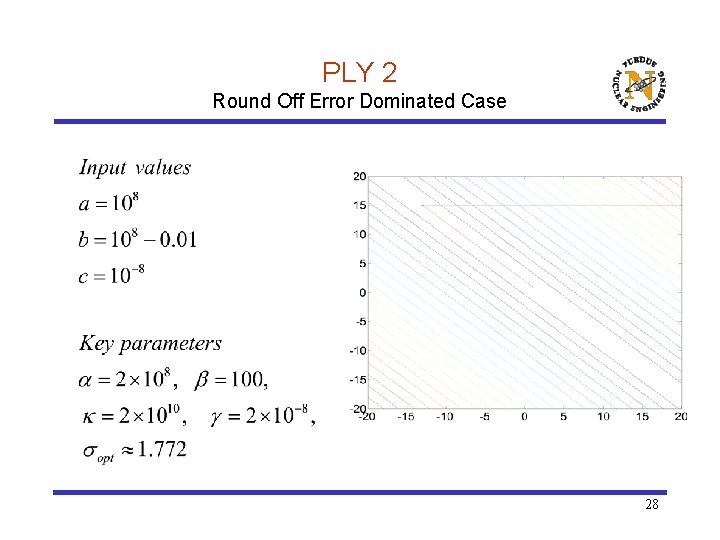
PLY 2 Round Off Error Dominated Case 28

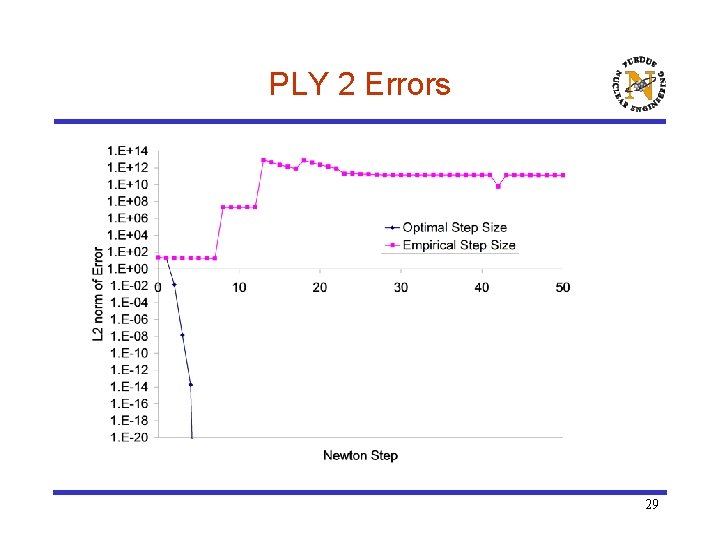
PLY 2 Errors 29

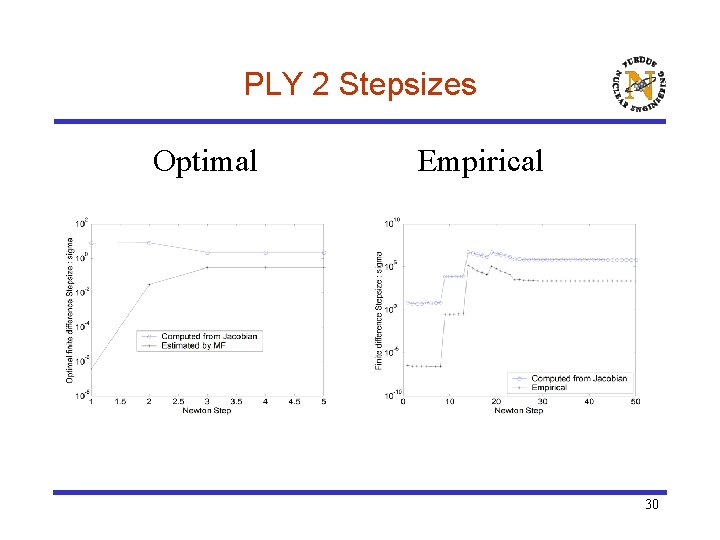
PLY 2 Stepsizes Optimal Empirical 30

PLY 2 Stepsize Parametric

Numerical Examples: Navier-Stokes-Like Problem (Goyon) ¨ PDE Diffusion Convection Non-physical Force function ¨ Boundary Condition ¨ Force function ¨ Goyon, Precoditioned Newton Methods using Incremental Unknowns Methods for Resolution of a Steady-State Navier-Stokes-Like Problem. Applied Mathematic and Computation, 87(1997), pp. 289 -311.

The Finite difference Equations

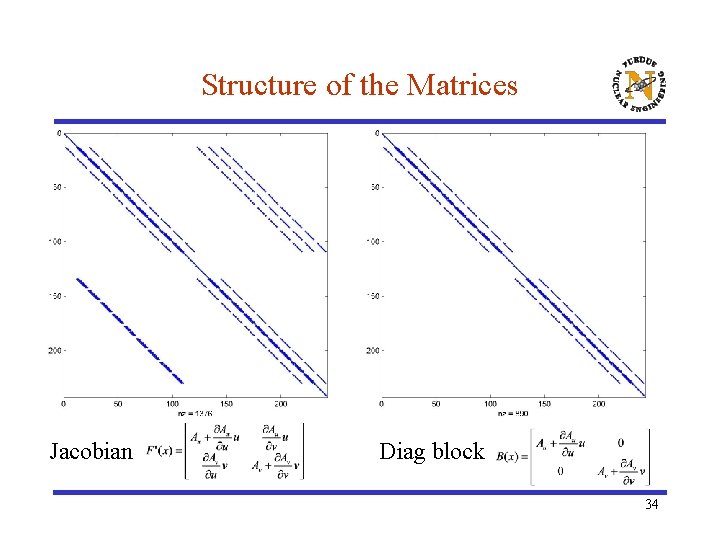
Structure of the Matrices Jacobian Diag block 34

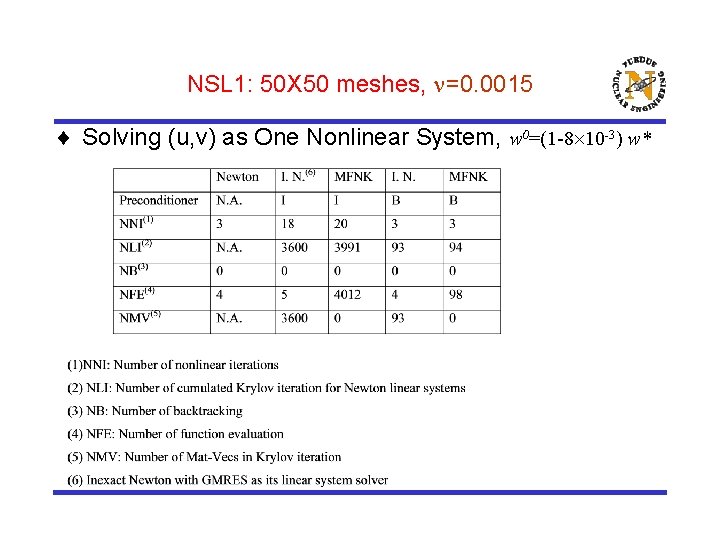
NSL 1: 50 X 50 meshes, =0. 0015 ¨ Solving (u, v) as One Nonlinear System, w 0=(1 -8 10 -3) w*

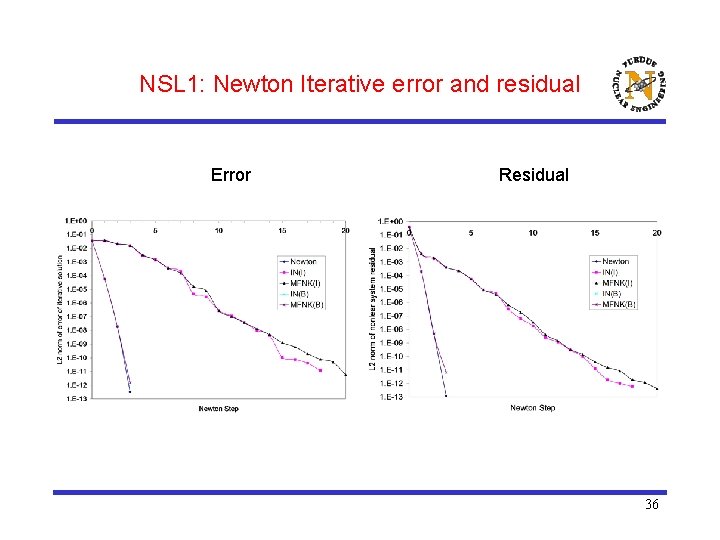
NSL 1: Newton Iterative error and residual Error Residual 36

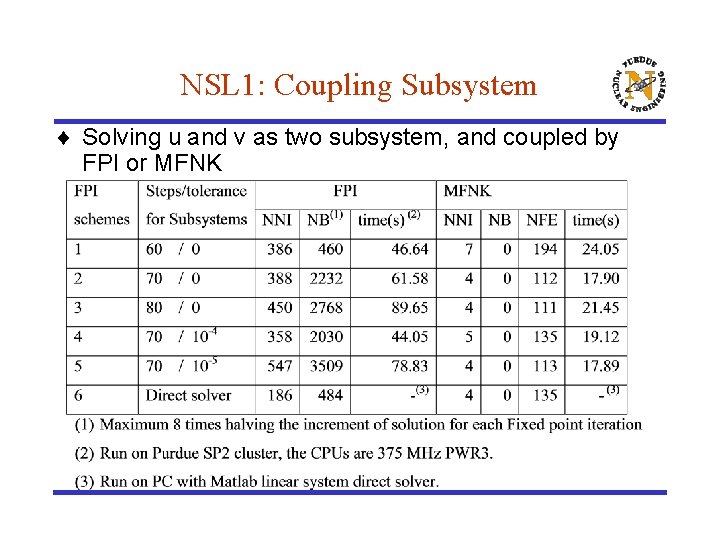
NSL 1: Coupling Subsystem ¨ Solving u and v as two subsystem, and coupled by FPI or MFNK

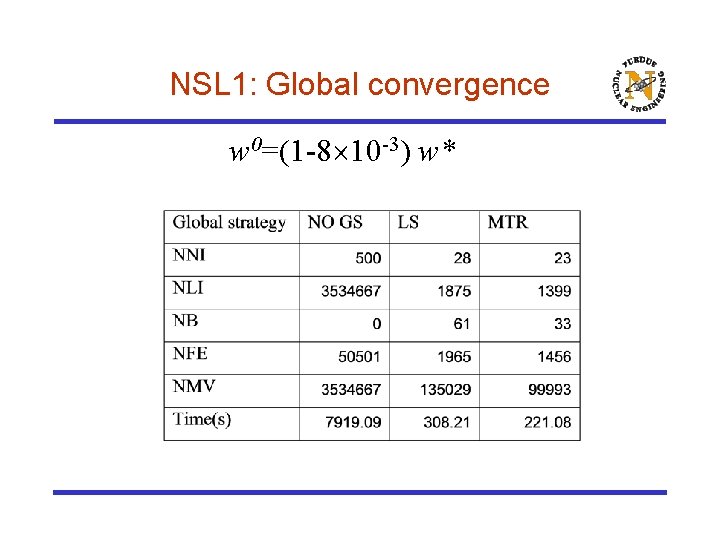
NSL 1: Global convergence w 0=(1 -8 10 -3) w*

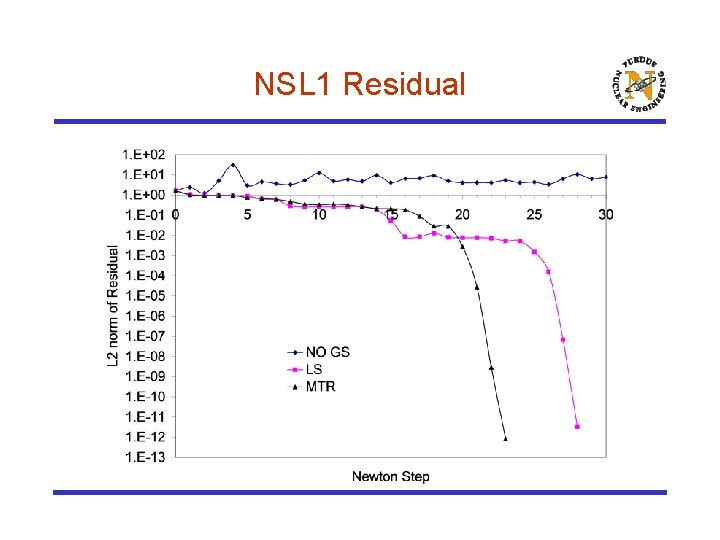
NSL 1 Residual

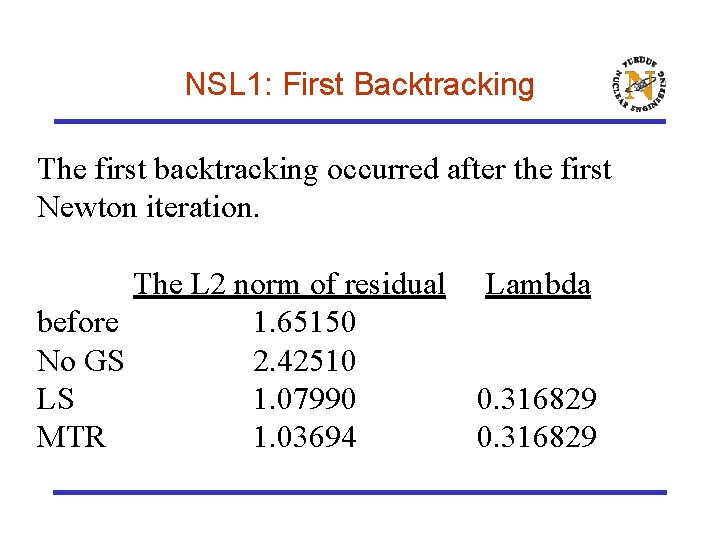
NSL 1: First Backtracking The first backtracking occurred after the first Newton iteration. The L 2 norm of residual Lambda before 1. 65150 No GS 2. 42510 LS 1. 07990 0. 316829 MTR 1. 03694 0. 316829

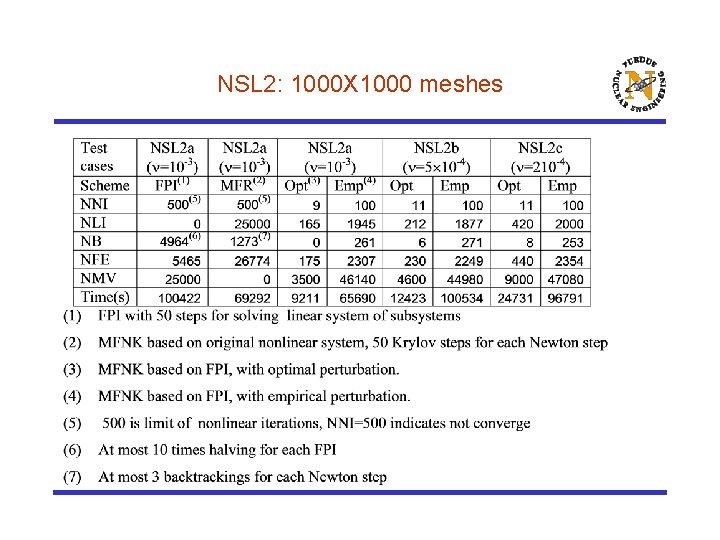
NSL 2: 1000 X 1000 meshes

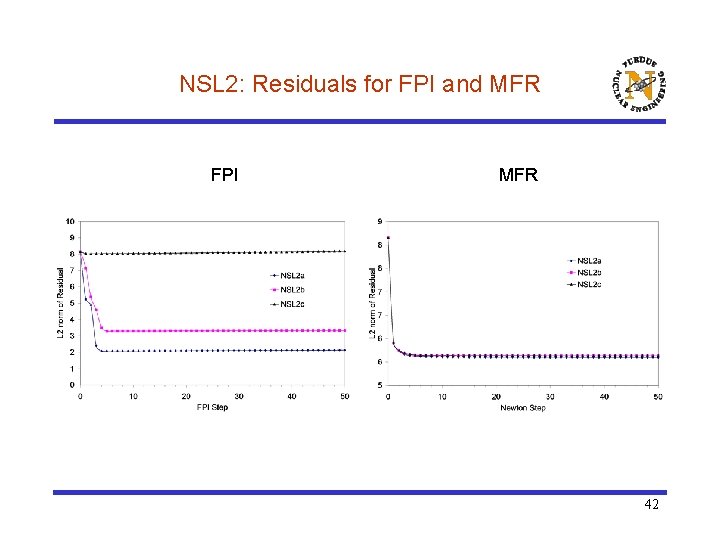
NSL 2: Residuals for FPI and MFR FPI MFR 42

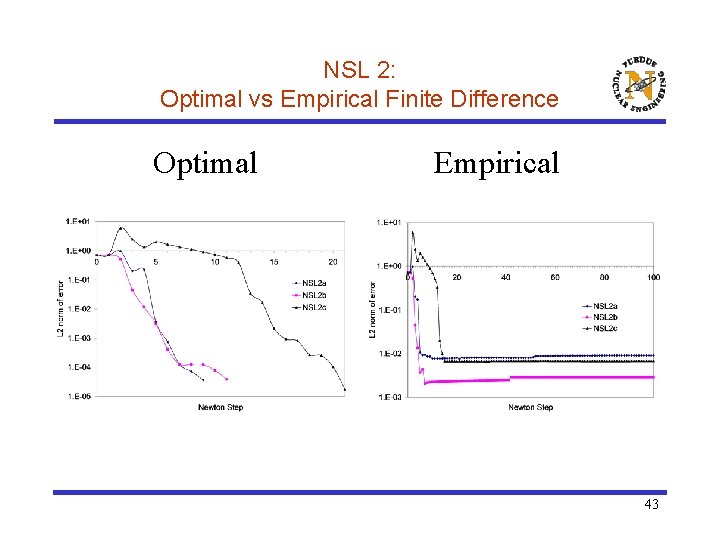
NSL 2: Optimal vs Empirical Finite Difference Optimal Empirical 43

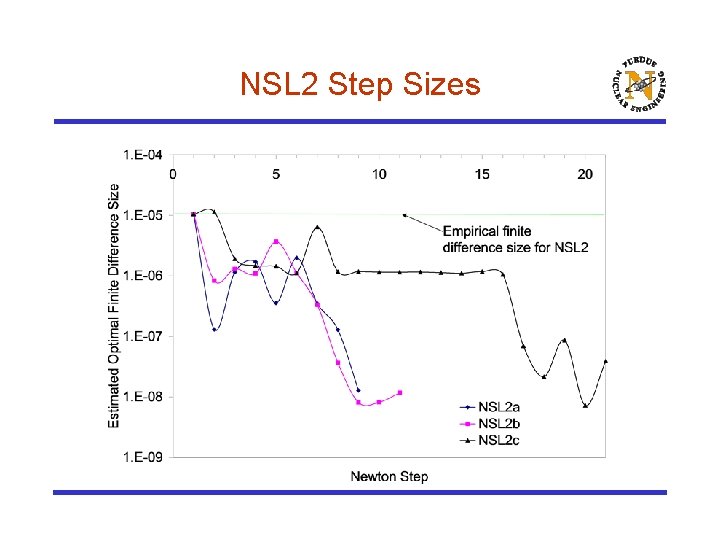
NSL 2 Step Sizes

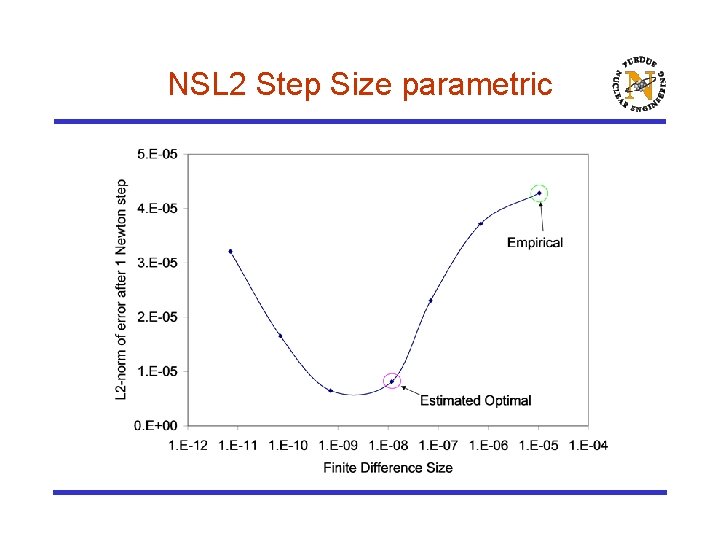
NSL 2 Step Size parametric

Summary ¨ A general approach, MFNK, was presented here for coupling subsystems with respective solvers. ¨ Based on any FPI, a corresponding MFNK method can be constructed. ¨ MFNK provides a more efficient method than FPI for coupling subsystems. ¨ MFNK can converge for several cases in which the corresponding FPI diverges. ¨ Locally, MFNK converges at least q-linearly and in many cases qquadratically. ¨ A more sophisticated FPI scheme provides a more efficient nonlinear system for the corresponding MFNK.

Summary (Cont. ) ¨ A method was proposed to estimate the optimal perturbation size for matrix free Newton/Krylov methods. ¨ The method was based on an analysis of the truncation error and the round-off error introduced by the finite difference approximation. ¨ The optimal perturbation size can be accurately estimated in the MFNK algorithm with almost no additional computational cost. ¨ Numerical examples shows that the optimum perturbation size leads to improved convergence of the MFNK method compared to the perturbation determined by empirical formulas.

Summary (Cont. ) ¨ Line Search and Model Trust Region, were implemented within the framework of MFNK – For the line search method, a quadratic or higher order model was used with an approximation for the gradient – For the model trust region strategy, a double dogleg approach was implemented using the projection of a Newton step and Cauchy point within the Krylov subspace – the model trust region strategy showed better local performance than the line search strategy ¨ Peer-to-Peer parallel MFNK algorithm was implemented