A MACHINE LEARNING APPROACH FOR AUTOMATIC STUDENT MODEL

A MACHINE LEARNING APPROACH FOR AUTOMATIC STUDENT MODEL DISCOVERY Nan Li, Noboru Matsuda, William Cohen, and Kenneth Koedinger Computer Science Department Carnegie Mellon University

STUDENT MODEL A set of knowledge components (KCs) Encoded in intelligent tutors to model how students solve problems � Example: What to do next on problems like 3 x=12 A key factor behind instructional decisions in automated tutoring systems 2

STUDENT MODEL CONSTRUCTION Traditional Methods � Structured interviews � Think-aloud protocols � Rational analysis Previous Automated Methods � Learning factor analysis (LFA) Require expert input. Highly subjective. Within the search space of human-provided factors. Proposed Approach � Use a machine-learning agent, Sim. Student, to acquire knowledge � 1 production rule acquired => 1 KC in student model (Q matrix) Independent of humanprovided factors. 3

A BRIEF REVIEW OF SIMSTUDENT • A machine-learning agent that • • • acquires production rules from examples & problem solving experience given a set of feature predicates & functions 4

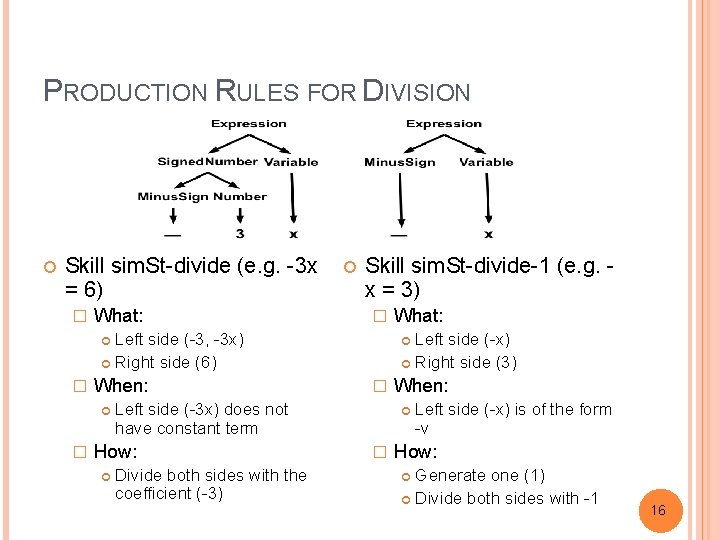
PRODUCTION RULES Skill divide (e. g. -3 x = 6) � What: Left side (-3 x) Right side (6) � When: Left side (-3 x) does not have constant term => � How: Get-coefficient (-3) of left side (-3 x) Divide both sides with the coefficient Each production rule is associated with one KC Each step (-3 x = 6) is labeled with one KC, decided by the production applied to that step Original model required strong domain-specific operators, like Get-coefficient Does not differentiate important distinctions in learning (e. g. , -x=3 vs -3 x = 6) 5

DEEP FEATURE LEARNING Expert vs Novice (Chi et al. , 1981) � Example: What’s the coefficient of -3 x? Expert uses deep functional features to reply -3 Novice may use shallow perceptual features to reply 3 Model deep feature learning using machine learning techniques Integrate acquired knowledge into Sim. Student learning Remove dependence on strong operators & split KCs into finer grain sizes 6

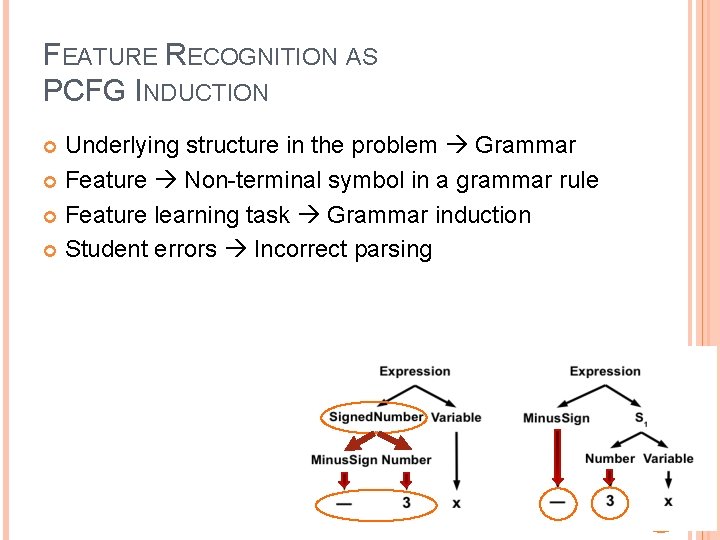
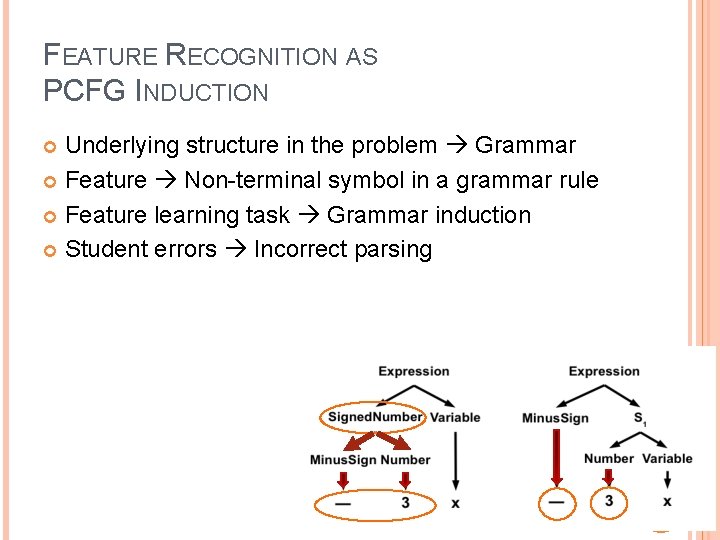
FEATURE RECOGNITION AS PCFG INDUCTION Underlying structure in the problem Grammar Feature Non-terminal symbol in a grammar rule Feature learning task Grammar induction Student errors Incorrect parsing 7

LEARNING PROBLEM Input is a set of feature recognition records consisting of � An original problem (e. g. -3 x) � The feature to be recognized (e. g. -3 in -3 x) Output �A probabilistic context free grammar (PCFG) � A non-terminal symbol in a grammar rule that represents target feature 8

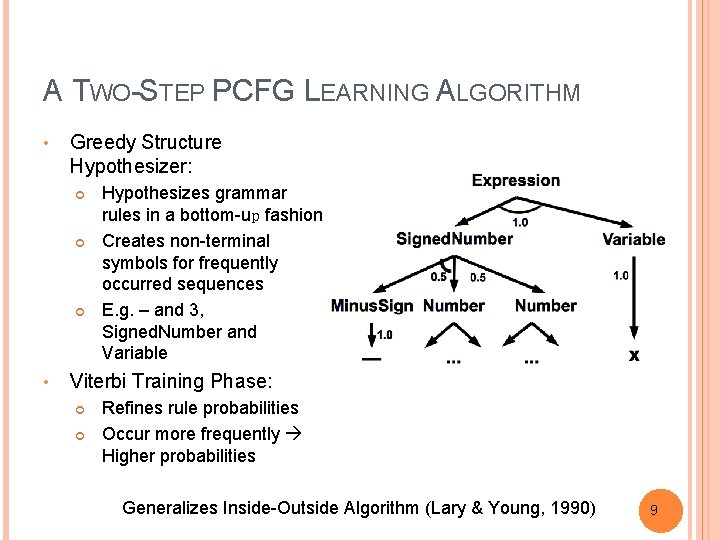
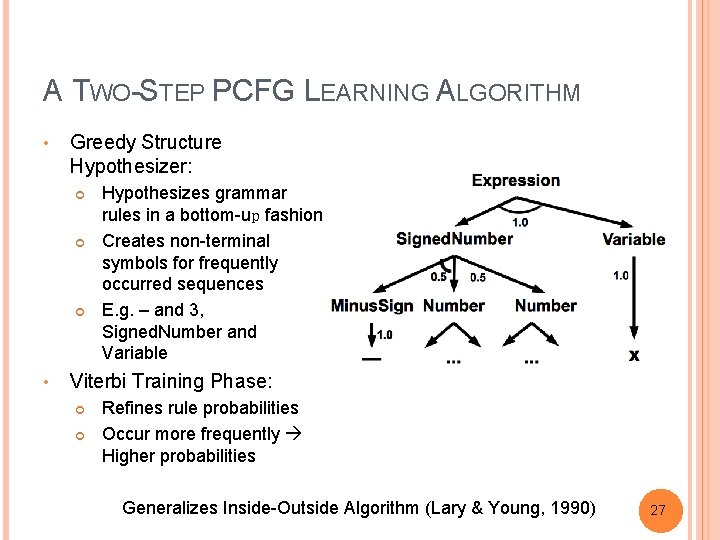
A TWO-STEP PCFG LEARNING ALGORITHM • Greedy Structure Hypothesizer: • Hypothesizes grammar rules in a bottom-up fashion Creates non-terminal symbols for frequently occurred sequences E. g. – and 3, Signed. Number and Variable Viterbi Training Phase: Refines rule probabilities Occur more frequently Higher probabilities Generalizes Inside-Outside Algorithm (Lary & Young, 1990) 9

EXAMPLE OF PRODUCTION RULES BEFORE AND AFTER INTEGRATION Extend the “What” Part in Production Rule Original: Extended: Skill divide (e. g. -3 x = 6) What: Left side (-3 x) Left side (-3, -3 x) Right side (6) When: Left side (-3 x) does not operators • Fewer have constant term • Eliminate need for => => domain-specific operators How: Get coefficient (-3) of left side (-3 x) Divide both sides with the coefficient (-3) 10

Original: Skill divide (e. g. -3 x = 6) What: Left side (-3 x) Right side (6) When: Left side (-3 x) does not have constant term => How: Get coefficient (-3) of left side (-3 x) Divide both sides with the coefficient (-3) 11

EXPERIMENT METHOD Sim. Student vs. Human-generated model Code real student data � 71 students used a Carnegie Learning Algebra I Tutor on equation solving � Sim. Student: Tutored by a Carnegie Learning Algebra I Tutor Coded each step by the applicable production rule Used human-generated coding in case of no applicable production � Human-generated model: Coded manually based on expertise 12

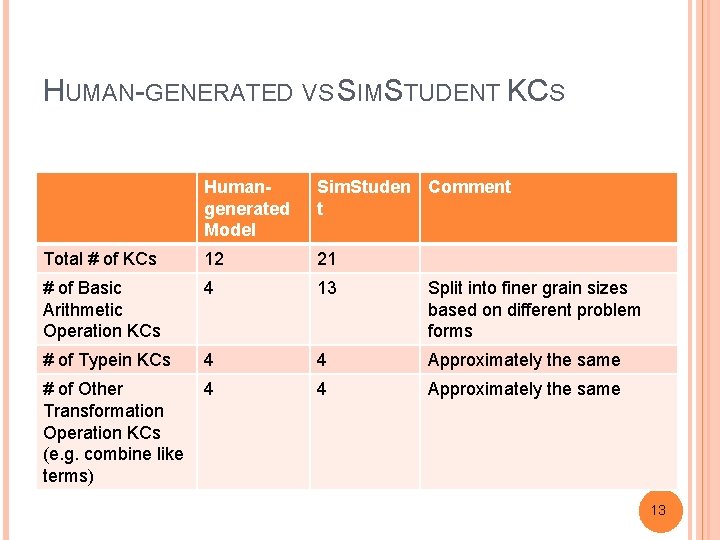
HUMAN-GENERATED VS SIMSTUDENT KCS Humangenerated Model Sim. Studen Comment t Total # of KCs 12 21 # of Basic Arithmetic Operation KCs 4 13 Split into finer grain sizes based on different problem forms # of Typein KCs 4 4 Approximately the same # of Other Transformation Operation KCs (e. g. combine like terms) 4 4 Approximately the same 13

HOW WELL TWO MODELS FIT WITH REAL STUDENT DATA Used Additive Factor Model (AFM) � An instance of logistic regression that � Uses each student, each KC and KC by opportunity interaction as independent variables � To predict probabilities of a student making an error on a specific step 14

AN EXAMPLE OF SPLIT IN DIVISION Human-generated Model � divide: Ax=B & -x=A Sim. Student � sim. St-divide: Ax=B � sim. St-divide-1: -x=A divide 1 1 1 1 1 sim. St-divide 1 1 1 1 0 0 0 sim. St-divide-1 0 0 0 0 1 1 1 Ax=B -x=A

PRODUCTION RULES FOR DIVISION Skill sim. St-divide (e. g. -3 x = 6) � What: Skill sim. St-divide-1 (e. g. x = 3) � Left side (-3, -3 x) Right side (6) Left side (-x) Right side (3) � When: � � Left side (-3 x) does not have constant term How: Divide both sides with the coefficient (-3) What: When: � Left side (-x) is of the form -v How: Generate one (1) Divide both sides with -1 16

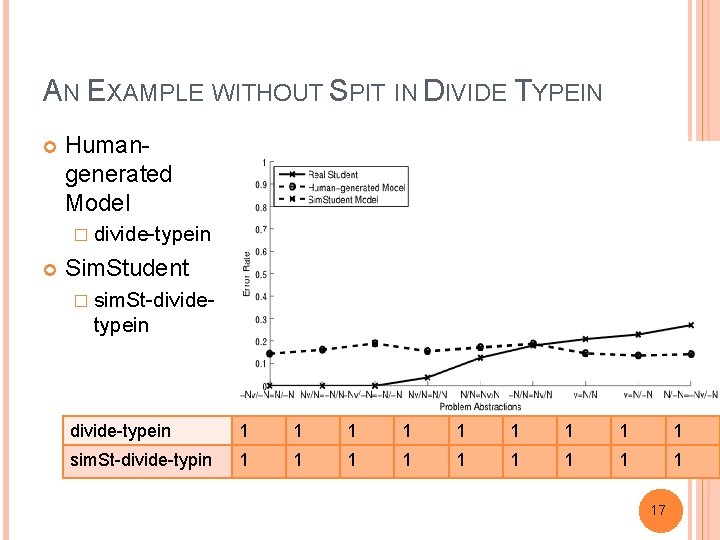
AN EXAMPLE WITHOUT SPIT IN DIVIDE TYPEIN Humangenerated Model � divide-typein Sim. Student � sim. St-divide- typein divide-typein 1 1 1 1 1 sim. St-divide-typin 1 1 1 1 17

SIMSTUDENT VS SIMSTUDENT + FEATURE LEARNING Sim. Student � Needs strong operators � Constructs student models similar to human-generated model Extended Sim. Student � Only requires weak operators � Split KCs into finer grain sizes based on different parse trees Does Extended Sim. Student produce a KC model that better fits student learning data? 18

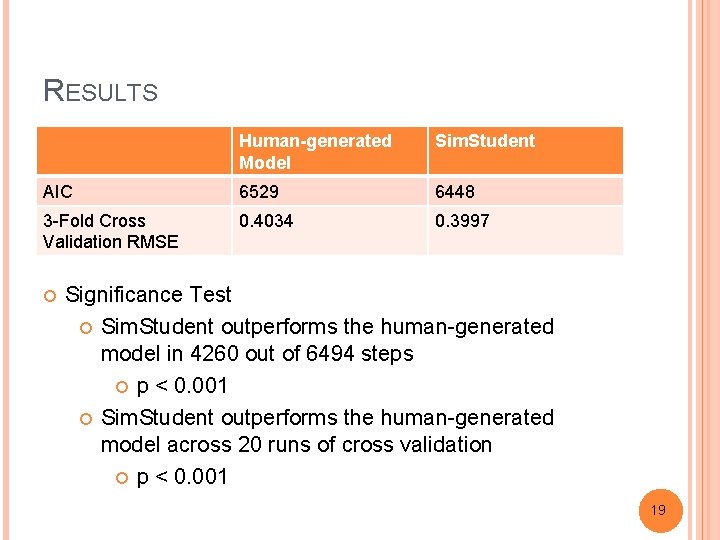
RESULTS Human-generated Model Sim. Student AIC 6529 6448 3 -Fold Cross Validation RMSE 0. 4034 0. 3997 Significance Test Sim. Student outperforms the human-generated model in 4260 out of 6494 steps p < 0. 001 Sim. Student outperforms the human-generated model across 20 runs of cross validation p < 0. 001 19

SUMMARY Presented an innovative application of a machinelearning agent, Sim. Student, for an automatic discovery of student models. Showed that a Sim. Student generated student model was a better predictor of real student learning behavior than a human-generate model. 20

FUTURE STUDIES Test generality in other datasets in Data. Shop Apply this proposed approach in other domains � Stoichiometry � Fraction addition 21

22

AN EXAMPLE IN ALGEBRA 23

FEATURE RECOGNITION AS PCFG INDUCTION Underlying structure in the problem Grammar Feature Non-terminal symbol in a grammar rule Feature learning task Grammar induction Student errors Incorrect parsing 24

LEARNING PROBLEM Input is a set of feature recognition records consisting of � An original problem (e. g. -3 x) � The feature to be recognized (e. g. -3 in -3 x) Output �A probabilistic context free grammar (PCFG) � A non-terminal symbol in a grammar rule that represents target feature 25

A COMPUTATIONAL MODEL OF DEEP FEATURE LEARNING Extended a PCFG Learning Algorithm (Li et al. , 2009) Feature Learning Stronger Prior Knowledge: � Transfer Learning Using Prior Knowledge 26

A TWO-STEP PCFG LEARNING ALGORITHM • Greedy Structure Hypothesizer: • Hypothesizes grammar rules in a bottom-up fashion Creates non-terminal symbols for frequently occurred sequences E. g. – and 3, Signed. Number and Variable Viterbi Training Phase: Refines rule probabilities Occur more frequently Higher probabilities Generalizes Inside-Outside Algorithm (Lary & Young, 1990) 27

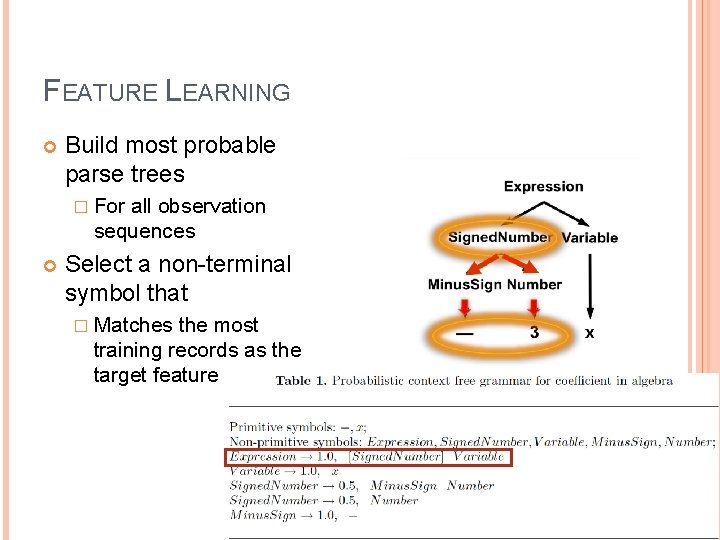
FEATURE LEARNING Build most probable parse trees � For all observation sequences Select a non-terminal symbol that � Matches the most training records as the target feature 28

TRANSFER LEARNING USING PRIOR KNOWLEDGE GSH Phase: � Build parse trees based on some previously acquired grammar rules � Then call the original GSH Viterbi Training: � Add rule frequency in previous task to the current task 0. 5 0. 33 0. 5 0. 66 29