A Lockfree Multithreaded Algorithm for the Maxflow Problem

A Lock-free Multi-threaded Algorithm for the Max-flow Problem Bo Hong Electrical and Computer Engineering Department Drexel University bohong@coe. drexel. edu http: //www. ece. drexel. edu/faculty/bohong

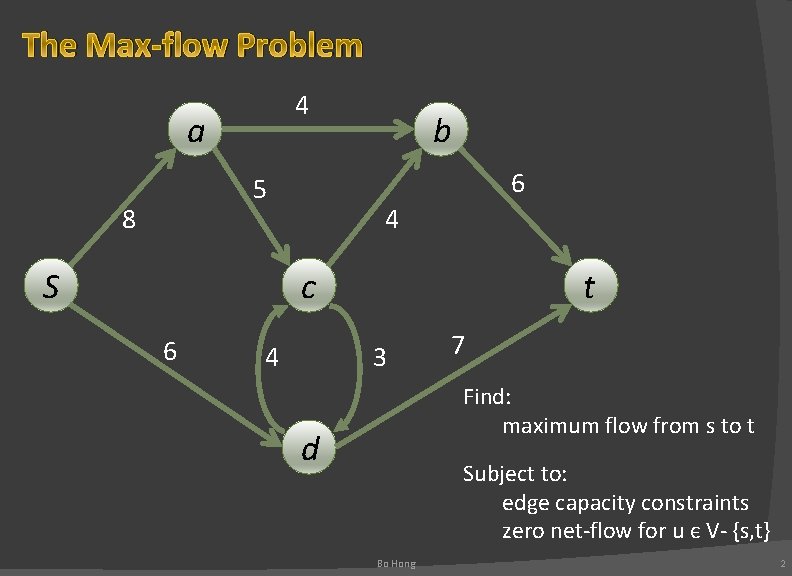
The Max-flow Problem 4 a 6 5 8 S b 4 c 6 4 t 3 7 Find: maximum flow from s to t d Subject to: edge capacity constraints zero net-flow for u є V- {s, t} Bo Hong 2

Existing algorithms � Sequential Algorithms � Augmenting Path ○ Ford-Fulkerson , pseudo-polynomial ○ Edmonds and Karp, O(|V|∙|E|2) ○ Dinitz, O(|V|2∙|E|) � Preflow Push ○ Karzanov, O(|V|3) � Push-Relabel ○ Goldberg, O(|V|2∙|E|), � with dynamic trees O(|V| ∙ |E| ∙ log(|V|2∙|E|) ) Parallel Algorithms � Shiloach, etc. O(|V|2 ∙log|V| ) with |V|-processor PRAM � Goldberg, O(|V|2 ∙log|V| ) with |V|-processor PRAM � Anderson, etc. Global relabeling � Bader, etc. Gap relabeling Bo Hong 3

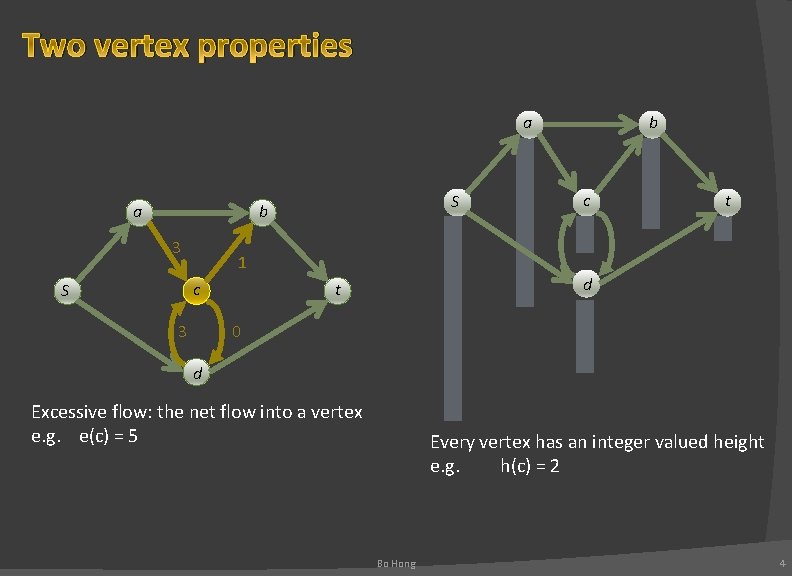
Two vertex properties a a S b 3 c t 1 c S b 3 d t 0 d Excessive flow: the net flow into a vertex e. g. e(c) = 5 Every vertex has an integer valued height e. g. h(c) = 2 Bo Hong 4

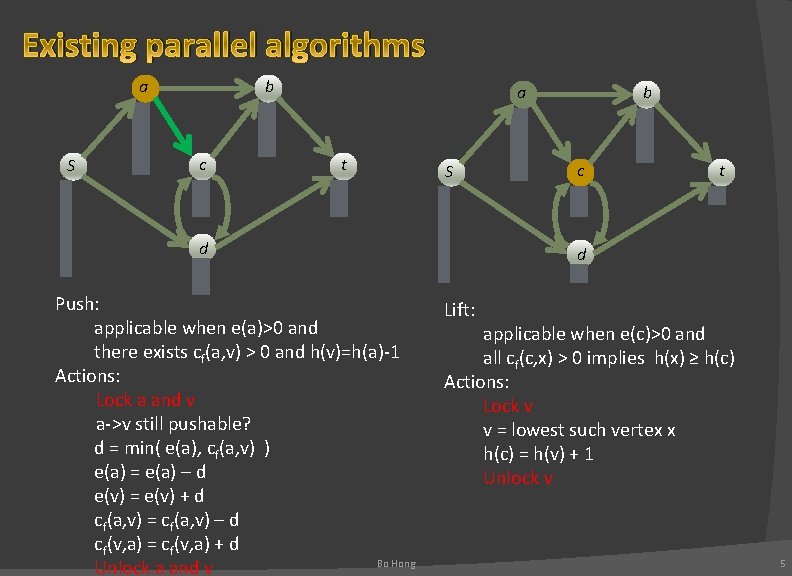
Existing parallel algorithms a S b c a t S d Push: applicable when e(a)>0 and there exists cf(a, v) > 0 and h(v)=h(a)-1 Actions: Lock a and v a->v still pushable? d = min( e(a), cf(a, v) ) e(a) = e(a) – d e(v) = e(v) + d cf(a, v) = cf(a, v) – d cf(v, a) = cf(v, a) + d Bo Hong Unlock a and v b c t d Lift: applicable when e(c)>0 and all cf(c, x) > 0 implies h(x) ≥ h(c) Actions: Lock v v = lowest such vertex x h(c) = h(v) + 1 Unlock v 5

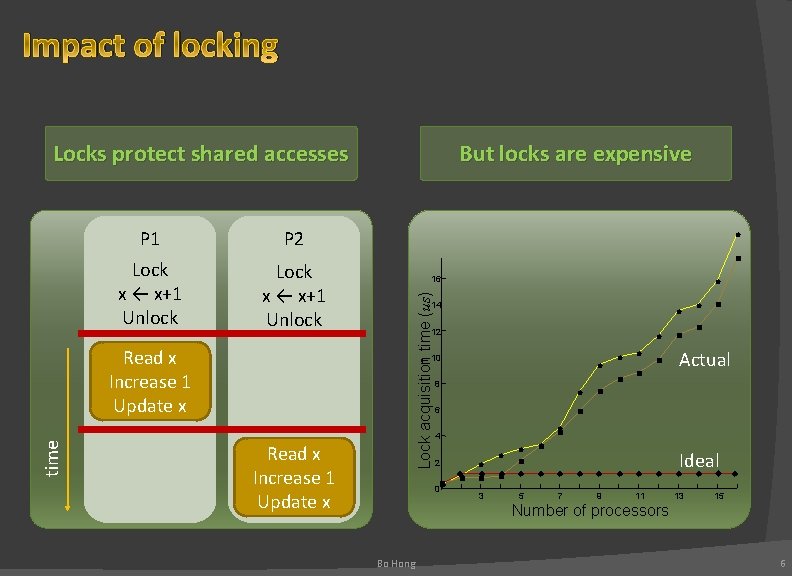
Impact of locking Locks protect shared accesses Lock x ← x+1 Unlock P 2 l n Lock x ← x+1 Unlock 16 Lock acquisition. T time (us) P 1 But locks are expensive 14 l 12 Read x Increase 1 Update x time l l 10 Read x Increase 1 Update x l n 8 l 6 n n n Actual n 2 n l n n 4 l 0 su l n l u n 3 l u n l n u 5 l n u u 7 u u 9 u u u 11 Ideal u 13 u u u 15 Number of processors Bo Hong 6

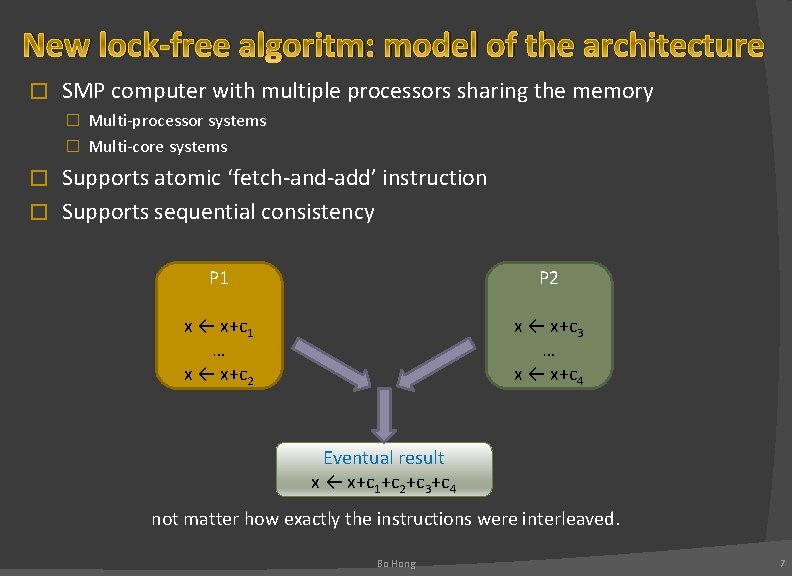
New lock-free algoritm: model of the architecture � SMP computer with multiple processors sharing the memory � Multi-processor systems � Multi-core systems Supports atomic ‘fetch-and-add’ instruction � Supports sequential consistency � P 1 P 2 x ← x+c 1 … x ← x+c 2 x ← x+c 3 … x ← x+c 4 Eventual result x ← x+c 1+c 2+c 3+c 4 not matter how exactly the instructions were interleaved. Bo Hong 7

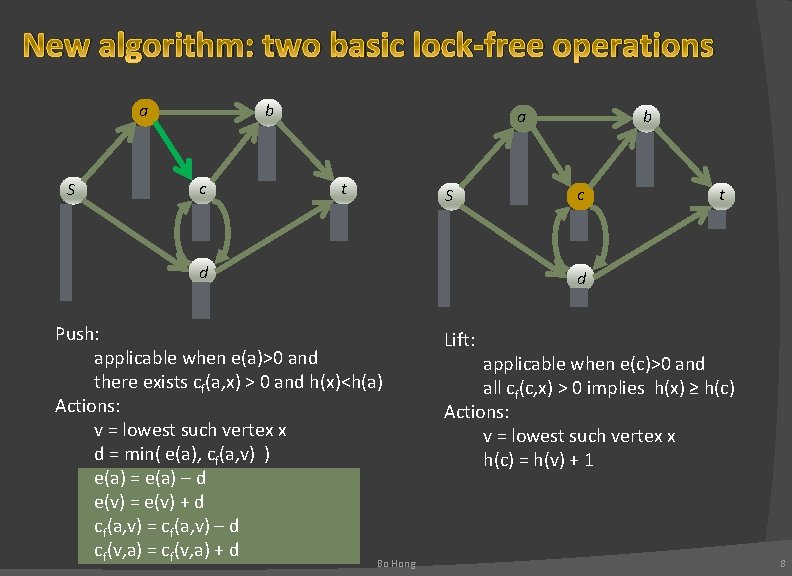
New algorithm: two basic lock-free operations a S b c a t S d b c t d Push: applicable when e(a)>0 and there exists cf(a, x) > 0 and h(x)<h(a) Actions: v = lowest such vertex x d = min( e(a), cf(a, v) ) e(a) = e(a) – d e(v) = e(v) + d cf(a, v) = cf(a, v) – d cf(v, a) = cf(v, a) + d Bo Hong Lift: applicable when e(c)>0 and all cf(c, x) > 0 implies h(x) ≥ h(c) Actions: v = lowest such vertex x h(c) = h(v) + 1 8

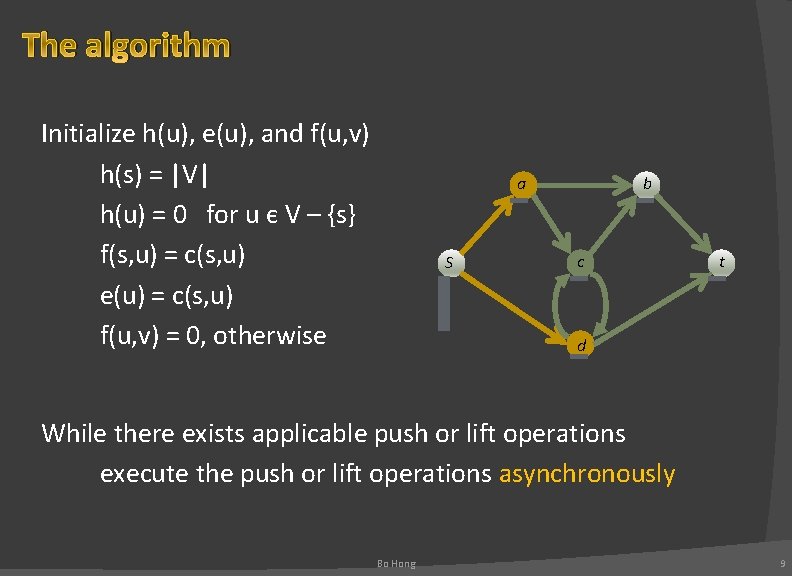
The algorithm Initialize h(u), e(u), and f(u, v) h(s) = |V| h(u) = 0 for u є V – {s} f(s, u) = c(s, u) e(u) = c(s, u) f(u, v) = 0, otherwise a S b c t d While there exists applicable push or lift operations execute the push or lift operations asynchronously Bo Hong 9

Asynchronous execution of the basic operations while e(u) > 0 P 1 e’ = e(u) h’ = ∞ for each (u, v) s. t. cf(u, v) > 0 if h(v) < h’ h’ = h(v) v’ = v if h(u) > h’ d = min ( e’, cf(u, v’) ) cf(u, v’) = cf(u, v’) + d cf(v’, u) = cf(v’, u) – d e(u) = e(u) – d e(v’) = e(v’) + d else h(u) = h’ + 1 while e(u) > 0 P 2 e’ = e(u) h’ = ∞ for each (u, v) s. t. cf(u, v) > 0 if h(v) < h’ h’ = h(v) v’ = v if h(u) > h’ d = min ( e’, cf(u, v’) ) cf(u, v’) = cf(u, v’) + d cf(v’, u) = cf(v’, u) – d e(u) = e(u) – d e(v’) = e(v’) + d else h(u) = h’ + 1 Bo Hong 10

or time while e(u) > 0 e’ = e(u) h’ = ∞ for each (u, v) s. t. cf(u, v) > 0 if h(v) < h’ h’ = h(v) v’ = v if h(u) > h’ d = min ( e’, cf(u, v’) ) cf(u, v’) = cf(u, v’) + d cf(v’, u) = cf(v’, u) – d e(u) = e(u) – d e(v’) = e(v’) + d else h(u) = h’ + 1 P 2 time Seems rather chaotic? . . . Not really P 1 Bo Hong 11

An invariant property of the algorithm As long as cf(u, v) and e(u) are updated atomically, we always have h(u) ≤ h(v) + 1 for any cf(u, v) > 0, no matter how the threads are interleaved. Bo Hong 12

Optimality of the algorithm � If any e(u) > 0, then the algorithm will not terminate Property of the push and lift operations � If the algorithm terminates, then there is no path from s to t in the residual graph Proof by contradiction, if such path exists, then the invariant property of function f has to be broken � If the algorithm terminates, it finds a maximum flow Termination implies all e(u)=0, meaning this is a feasible flow. No path from s to t, by max-flow min-cut theorem, it has to be a maximum flow Bo Hong 13

Convergence of the algorithm (complexity bound) � For any u s. t. e(u) > 0, there exists a path from u to s in the residual graph Property of network flow � The height of any vertex is less than 2|V| - 1 The longest path can have at most |V| vertices � The total number of lift operations is bound by 2|V|2 -|V| Bound by the height of vertices � The total number of saturated pushes is bound by (2|V|-1)∙|E| Bound by the total number of lift operations � The total number of un-saturated pushes is bound by 4|V|2 ∙|E| Bound by the number of lift and saturated pushes � Therefore the algorithm terminates with O(|V|2 ∙|E|) operations Bo Hong 14

Lock-free termination detection � The algorithm terminates when e(u) = 0 for all u є V – {s, t} � e(u) = 0 at a single thread is insufficient to terminate thread � An elegant solution: �The net flow out of source s decreases monotonically �The net flow into sink t increases monotonically �When the two values become equal, we must have e(u) = 0 for all u є V – {s, t}, a necessary and sufficient termination condition. Bo Hong 15

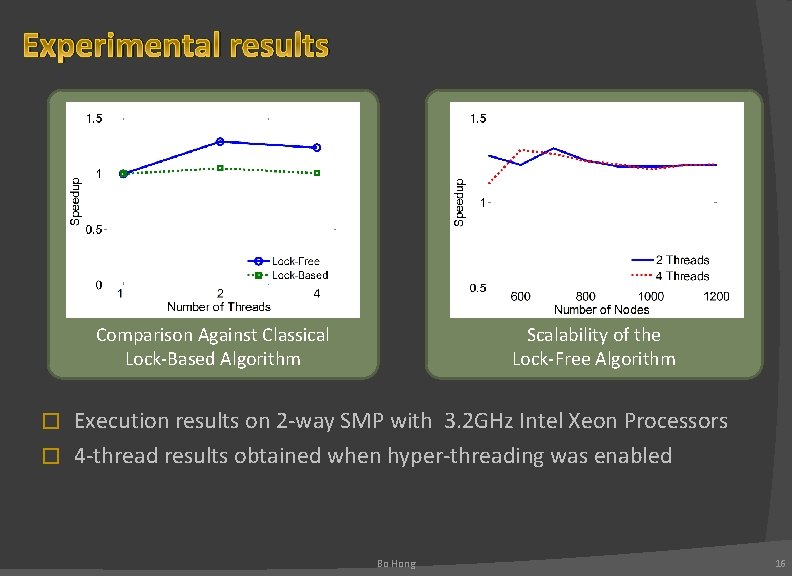
Experimental results Comparison Against Classical Lock-Based Algorithm Scalability of the Lock-Free Algorithm Execution results on 2 -way SMP with 3. 2 GHz Intel Xeon Processors � 4 -thread results obtained when hyper-threading was enabled � Bo Hong 16

Summary and future work � Developed a lock-free multi-threaded algorithm for the max-flow problem � having the same complexity bound as existing parallel algorithms � eliminated lock usages thereby improving thread-level parallelism � 20% improvement over existing lock-based parallel algorithms � Results indicate the effectiveness of algorithmic method in reducing synchronization overheads � Future work � Load balancing across the threads: vertex to thread assignment, static or dynamic or hybrid? � Optimize cache usages � Reduce the number of operations via global and gap relabling � What if edge capacities are floating-point? Bo Hong 17