A Linear Inequality in One Variable A linear

A Linear Inequality in One Variable A linear inequality in one variable, x, is defined as any relationship of the form: ax + b < c, ax + b ≤ c, ax + b > c, or ax + b ≥ c, where, a ≠ 0.

A Linear Inequality in One Variable

A Linear Inequality in One Variable

Addition and Subtraction Properties of Inequality Let a, b, and c represent real number. *Addition property of inequality: If a < b Then a + c < b + c *Subtraction property of inequality: If a < b Then a − c < b − c *These properties may also be stated for a ≤ b, a > b, and a ≥ b.

Solving a Linear Inequality Solve the inequality. 3 x − 7 > 2(x − 4) − 1 Solution: 3 x − 7 > 2 x − 8 − 1 3 x − 7 > 2 x − 9 3 x − 2 x − 7 > 2 x − 9 x − 7 > − 9 x − 7 + 7 > − 9 + 7 x > − 2

Solving a Linear Inequality Set-builder notation: {x | x > − 2} Interval notation: (− 2, ∞)

Multiplication and Division Properties of Inequality Let a, b, and c represent real numbers. *if c is positive and a < b, then *If c is negative and a < b, then The second statement indicates that if both sides of an inequality are multiplied or divided by a negative quantity, the inequality sign must be reversed. *These properties may also be stated for a ≤ b, a > b, and a ≥ b.

Solving a Linear Inequality Solve the inequality. − 2 x − 5 < 2 Solution: − 2 x − 5 < 2 − 2 x − 5 + 5 < 2 + 5 − 2 x < 7

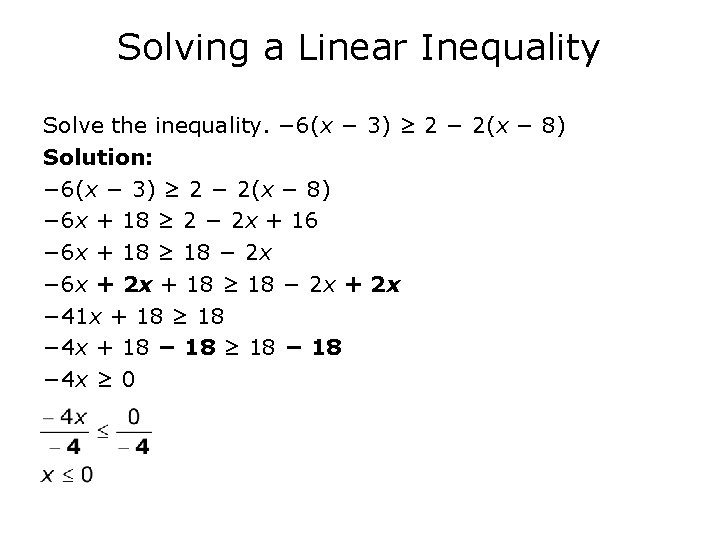
Solving a Linear Inequality Solve the inequality. − 6(x − 3) ≥ 2 − 2(x − 8) Solution: − 6(x − 3) ≥ 2 − 2(x − 8) − 6 x + 18 ≥ 2 − 2 x + 16 − 6 x + 18 ≥ 18 − 2 x − 6 x + 2 x + 18 ≥ 18 − 2 x + 2 x − 41 x + 18 ≥ 18 − 4 x + 18 − 18 ≥ 18 − 4 x ≥ 0

Solving a Linear Inequality Set-builder notation: {x | x ≤ 0} Interval notation: (−∞, 0]

Solving a Linear Inequality Solve the inequality Solution:

Solving a Linear Inequality Set-builder notation: {x | x > 4} Interval notation: (4, ∞)

Solving a Linear Inequality Application Beth received grades of 97, 82, 89, and 99 on her first four algebra tests. To earn an A in the course, she needs an average of 90 or more. What scores can she receive on the fifth test to earn an A? Solution: Let x represent the score on the fifth test. (Average of test scores) ≥ 90

Solving a Linear Inequality Application To earn an A, Beth would have to score at least 83 on her fifth test.

Definition of A Union B and A Intersection B • The union of sets A and B, denoted is the set of elements that belong to set A or to set B or to both sets A and B. • The intersection of two sets A and B, denoted is the set of elements common to both A and B.

Finding the Union and Intersection of Sets Given the sets: A = {x | x < 3} B = {x | x ≥ − 2} C = {x | x ≥ 5} Graph the following sets. Then express each set in interval notation.

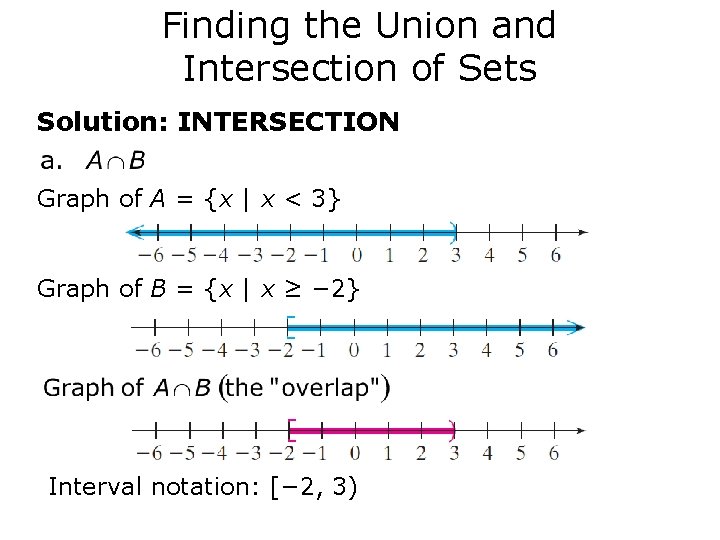
Finding the Union and Intersection of Sets Solution: INTERSECTION Graph of A = {x | x < 3} Graph of B = {x | x ≥ − 2} Interval notation: [− 2, 3)

Example 2: Finding the Union and Intersection of Sets (3 of 3) Solution: UNION Graph of A = {x | x < 3} Graph of C = {x | x ≥ 5}

Finding the Union and Intersection of Two Intervals Find the union or intersection as indicated. Write the answer in interval notation.

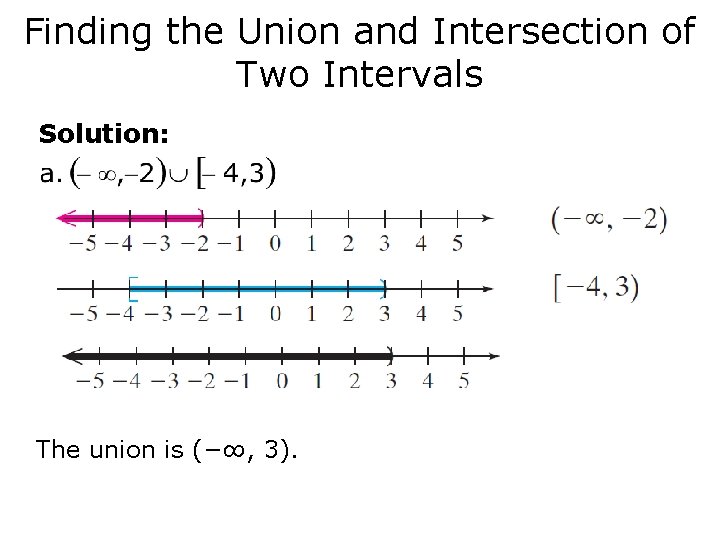
Finding the Union and Intersection of Two Intervals Solution: The union is (−∞, 3).

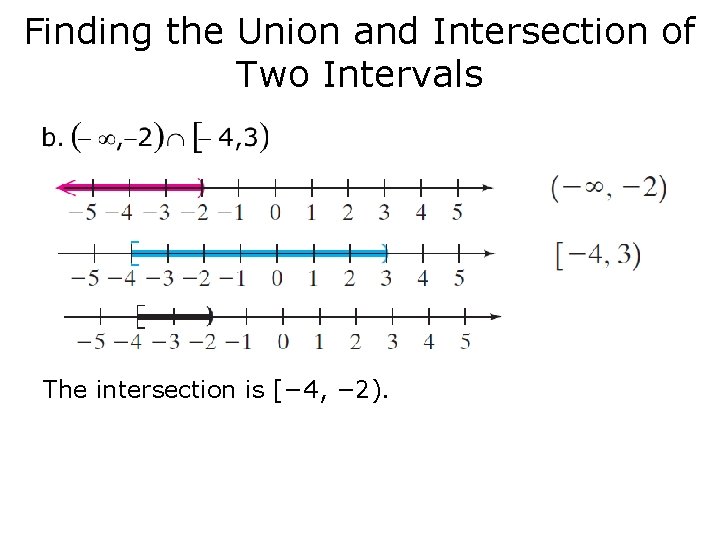
Finding the Union and Intersection of Two Intervals The intersection is [− 4, − 2).

Solving a Compound Inequality: And Step 1 Solve and graph each inequality separately. Step 2 If the inequalities are joined by the word and, find the intersection of the two solution sets. Step 3 Express the solution set in interval notation or in set-builder notation.

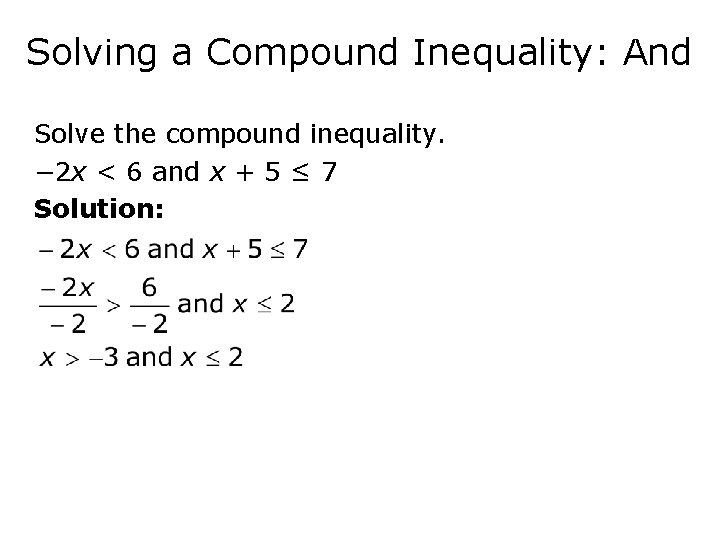
Solving a Compound Inequality: And Solve the compound inequality. − 2 x < 6 and x + 5 ≤ 7 Solution:

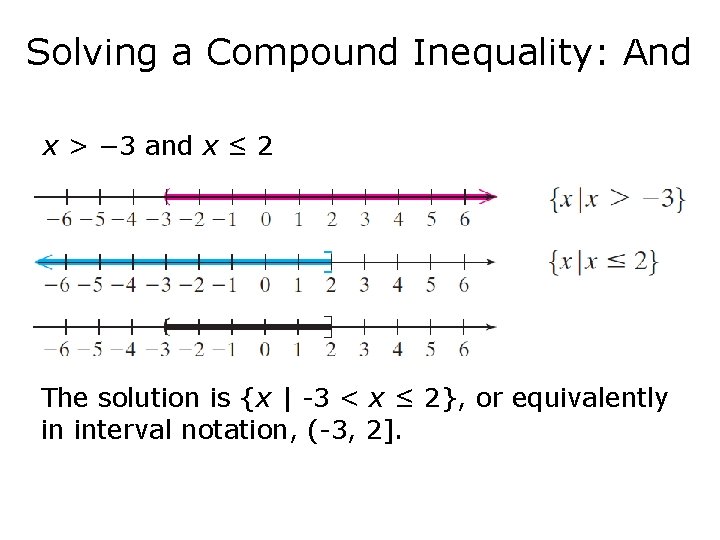
Solving a Compound Inequality: And x > − 3 and x ≤ 2 The solution is {x | -3 < x ≤ 2}, or equivalently in interval notation, (-3, 2].

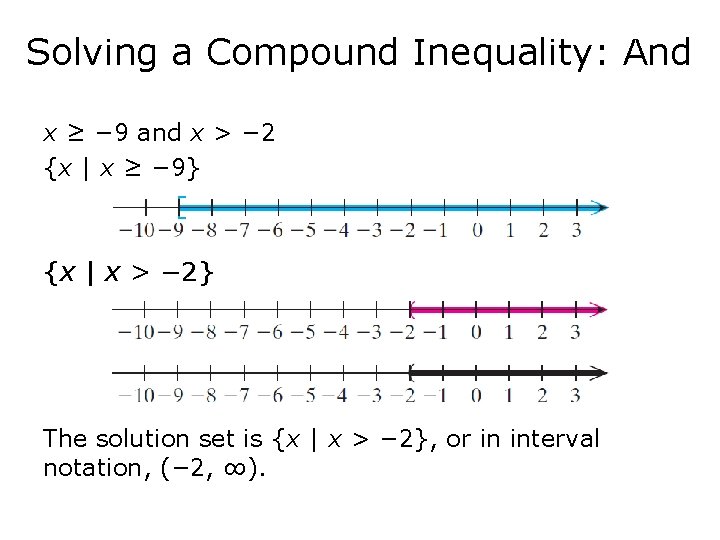
Solving a Compound Inequality: And x ≥ − 9 and x > − 2 {x | x ≥ − 9} {x | x > − 2} The solution set is {x | x > − 2}, or in interval notation, (− 2, ∞).

Solving an Inequality of the Form a < x < b Solve the inequality. − 4 < 3 x + 5 ≤ 10 Solution:

Solving an Inequality of the Form a < x < b

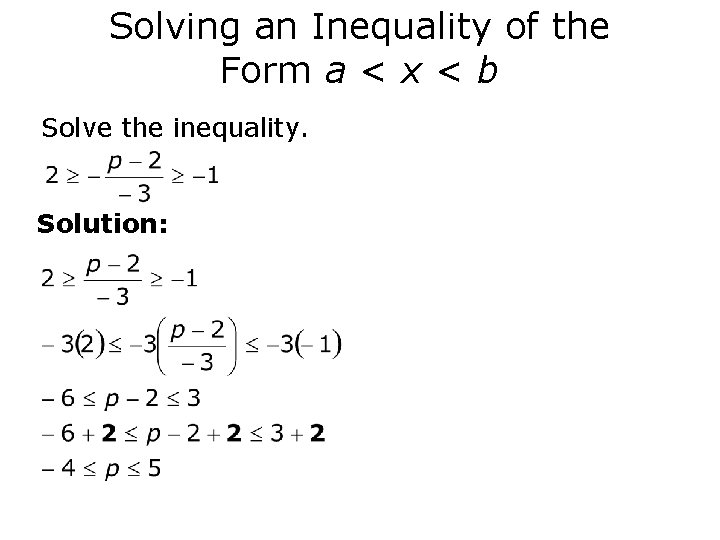
Solving an Inequality of the Form a < x < b Solve the inequality. Solution:

Solving an Inequality of the Form a < x < b − 4 ≤ p ≤ 5 The solution is {p | − 4 ≤ p ≤ 5}, or equivalently in interval notation [− 4, 5].

Solving a Compound Inequality: Or Step 1 Solve and graph each inequality separately. Step 2 If the inequalities are joined by the word or, find the union of the two solution sets. Step 3 Express the solution set in interval notation or in set-builder notation.

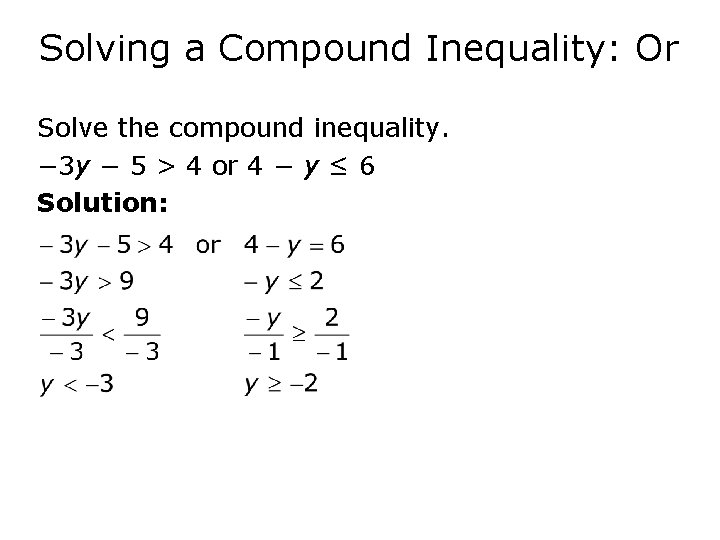
Solving a Compound Inequality: Or Solve the compound inequality. − 3 y − 5 > 4 or 4 − y ≤ 6 Solution:

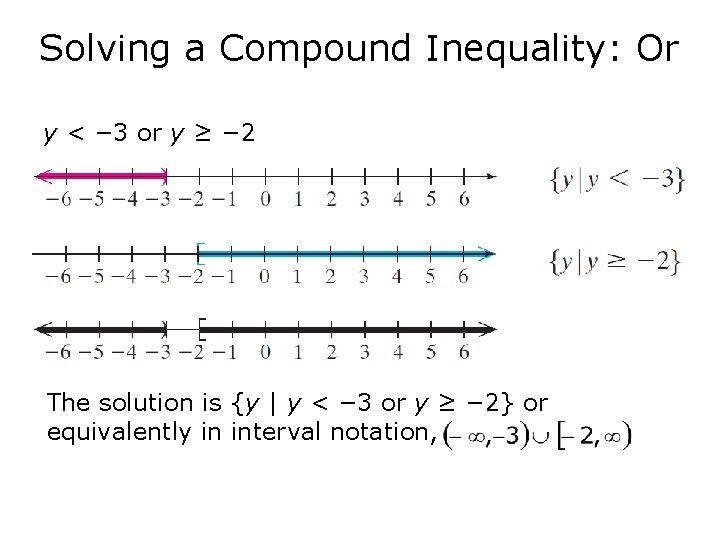
Solving a Compound Inequality: Or y < − 3 or y ≥ − 2 The solution is {y | y < − 3 or y ≥ − 2} or equivalently in interval notation,

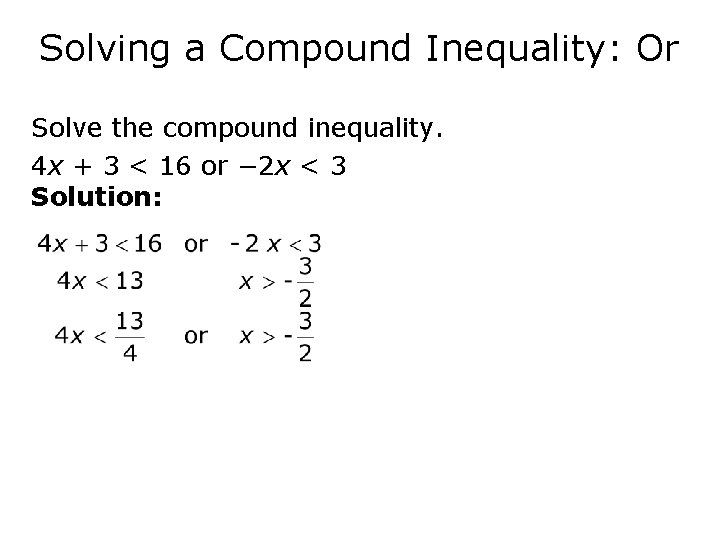
Solving a Compound Inequality: Or Solve the compound inequality. 4 x + 3 < 16 or − 2 x < 3 Solution:

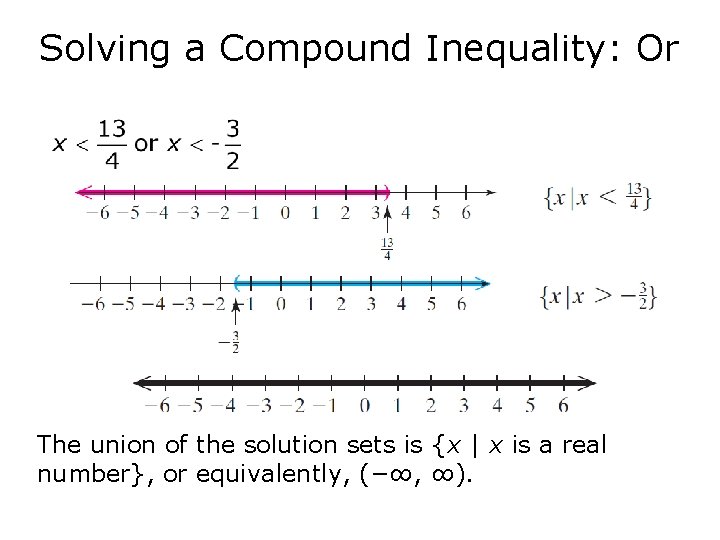
Solving a Compound Inequality: Or The union of the solution sets is {x | x is a real number}, or equivalently, (−∞, ∞).

Translating and Solving a Compound Inequality The sum of a number and 4 is between − 5 and 12. Find all such numbers. Solution: Let x represent a number. − 5 < x + 4 < 12 − 5 − 4 < x + 4 − 4 < 12 − 4 − 9 < x < 8 The number may be any real number between − 9 and 8: {x | − 9 < x < 8}.