A Level Physics Solid Materials Force Extension and

A –Level Physics: Solid Materials: Force. Extension and Stress-Strain Graphs

Objectives: 53. be able to use the Hooke’s law equation, ΔF = kΔx, where k is the stiffness of the object 54. understand how to use the relationships • ● (tensile/compressive) stress = force/cross-sectional area • ● (tensile/compressive) strain= change in length/original length • ● Young modulus = stress/strain Additional skills gained: • Calculating the gradient of a graphical representation • Identifying the value of the stiffness constant (k)

Starter: Calculate stiffness A ductile wire obeys Hooke’s law with the limit of proportionality of 16 N. At this point, the wire has extended from 20. 50 cm to 22. 49 cm. Sketch a Force-extension graph for this wire and calculate the value of the stiffness constant You have 10 mins ONLY Extension: Sketch another force-extension graph for a wire that is stronger but more brittle

Stress In physics, when stress is applied to a material, the material will be put under strain (i. e. strain is the result of stress) This is a little like force and extension except this time, it takes into account the area of the material; so that it’s specific to the type of the material that is used and is not specific to a certain dimension

Strain In physics, when stress is applied to a material, the material will be put under strain (i. e. strain is the result of stress) Strain is simply the extension (change in length) over the original length. Note that it has no unit as it’s a ratio of two lengths. It’s usually given as a percentage so don’t forget to convert that (e. g. 2% 0. 02)

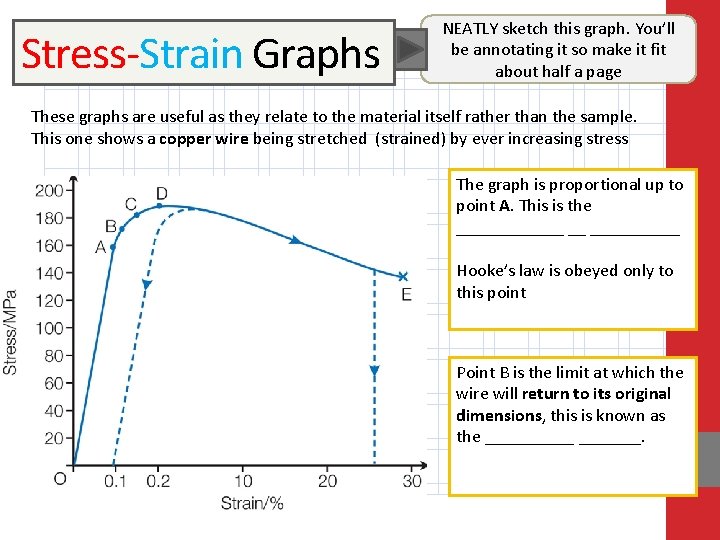
Stress-Strain Graphs NEATLY sketch this graph. You’ll be annotating it so make it fit about half a page These graphs are useful as they relate to the material itself rather than the sample. This one shows a copper wire being stretched (strained) by ever increasing stress The graph is proportional up to point A. This is the ______ __ _____ Hooke’s law is obeyed only to this point Point B is the limit at which the wire will return to its original dimensions, this is known as the _______.

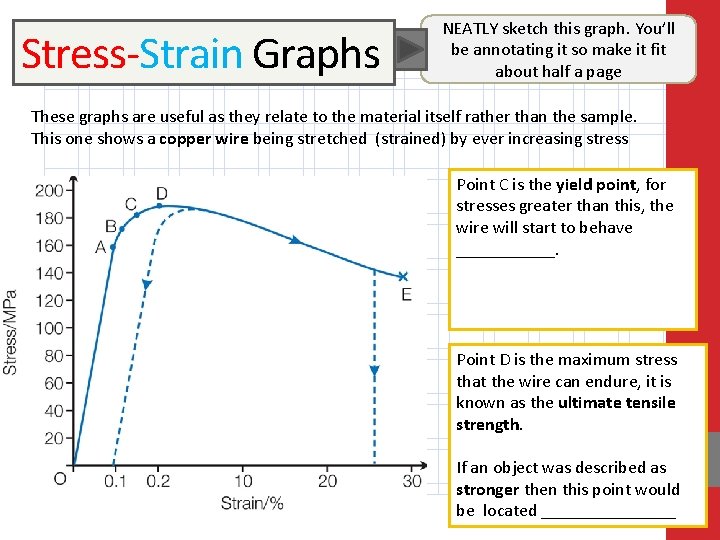
Stress-Strain Graphs NEATLY sketch this graph. You’ll be annotating it so make it fit about half a page These graphs are useful as they relate to the material itself rather than the sample. This one shows a copper wire being stretched (strained) by ever increasing stress Point C is the yield point, for stresses greater than this, the wire will start to behave ______. Point D is the maximum stress that the wire can endure, it is known as the ultimate tensile strength. If an object was described as stronger then this point would be located ________

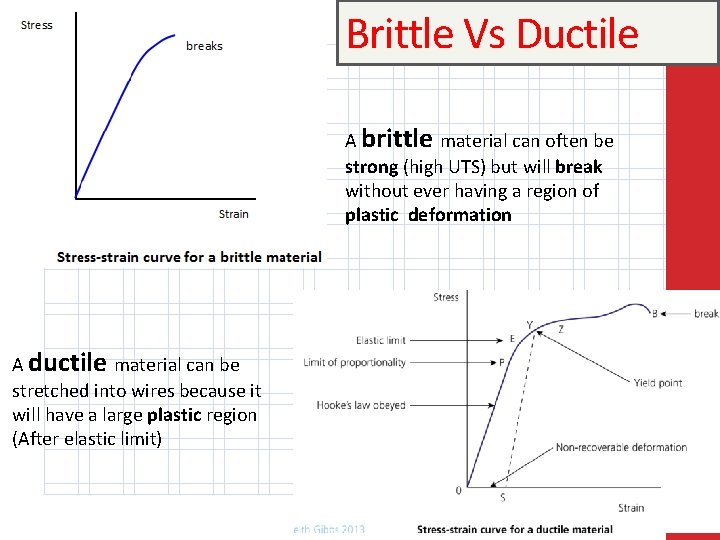
Brittle Vs Ductile A brittle material can often be strong (high UTS) but will break without ever having a region of plastic deformation A ductile material can be stretched into wires because it will have a large plastic region (After elastic limit)

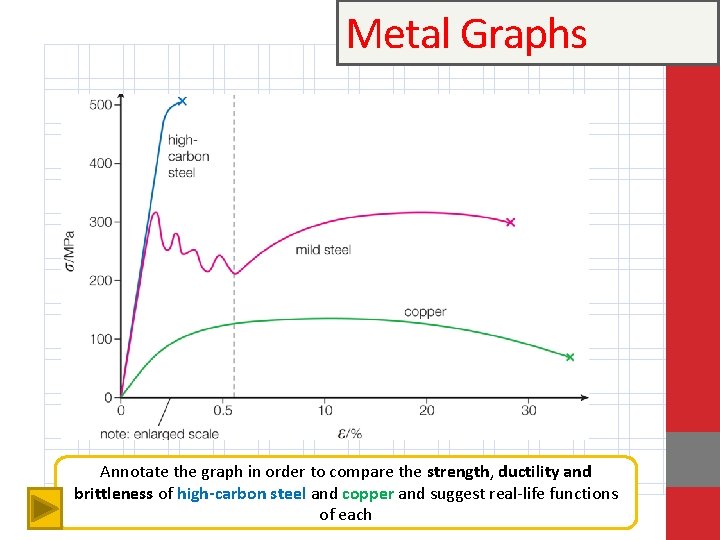
Metal Graphs Annotate the graph in order to compare the strength, ductility and brittleness of high-carbon steel and copper and suggest real-life functions of each

Young’s Modulus Named after Thomas Young, Young’s modulus is the measure of the stiffness of a material but taking into account the dimensions. I. e. it’s like the stiffness constant but for a stress-strain graph!

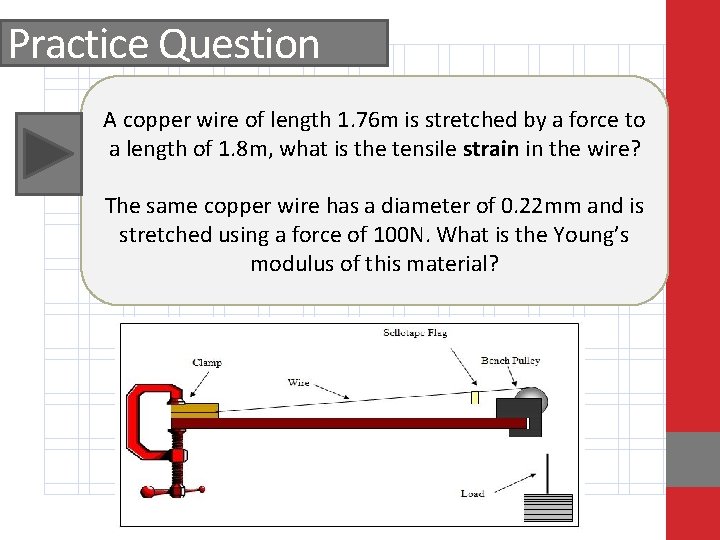
Practice Question A copper wire of length 1. 76 m is stretched by a force to a length of 1. 8 m, what is the tensile strain in the wire? The same copper wire has a diameter of 0. 22 mm and is stretched using a force of 100 N. What is the Young’s modulus of this material?

Practice Question Sheet Complete the ‘solid material’ practice sheet questions

Objectives: 53. be able to use the Hooke’s law equation, ΔF = kΔx, where k is the stiffness of the object 54. understand how to use the relationships • ● (tensile/compressive) stress = force/cross-sectional area • ● (tensile/compressive) strain= change in length/original length • ● Young modulus = stress/strain Additional skills gained: • Calculating the gradient of a graphical representation • Identifying the value of the stiffness constant (k)