A Level Physics Project OCR Physics A Physics

A Level Physics Project OCR Physics A Physics Core Concepts An introduction…

Week 1 session 1 Rearranging equations, standard form, conversions, units, significant figures

Symbols and SI units Changes at A Level • One of the highest jumps between GCSE and AS physics is the way things are written down. At AS level you’re expected to start using standard scientific notation. Standard notation means: • using the conventional symbols for quantities • writing all quantities in terms of SI units (Système International) • writing very large and very small numbers in standard form (e. g. 10– 6 instead of 0. 000001) • You will need to have memorised the unit prefixes shown in the table on the right – they are used in exams and it is assumed that you know what they mean. . Eg G is x 109 • Please watch the video below; • Clip 1 - click to open For example 4 ms is 4 x 10 -3 s or 0. 004 s Or 5 km is 5 x 103 m or 5000 m

Symbols and SI units Task 1 In the following ten pairs of quantities, circle the quantity which is greater. a. 12 m. W or 12 MW b. 3. 0 μs or 3. 0 ns c. 27 k. V or 27 GV d. 6 pm or 6μm e. 1024 TW or 1024 GW f. 22 x 10– 2 Ω or 220 Ω g. 300 kg or 3 x 103 kg h. 121 k. N or 0. 0121 x 106 N i. 30 x 10– 6 F or 0. 003 p. F j. 14000 MHz or 1. 4 x 109 Hz

Symbols and SI units Task 2: Solve the following: 1. How many metres in 2. 4 km? 2. How many joules in 8. 1 MJ? 3. Convert 326 GW into W 4. Convert 54 600 mm into m. 5. Convert 0. 18 nm into m. 6. Convert 632 nm into m. Express in standard form. 7. Convert 1002 m. V into V. Express in standard form. 8. How many e. V in 0. 511 Me. V? Express in standard form. 9. How many m in 11 km? Express in standard form

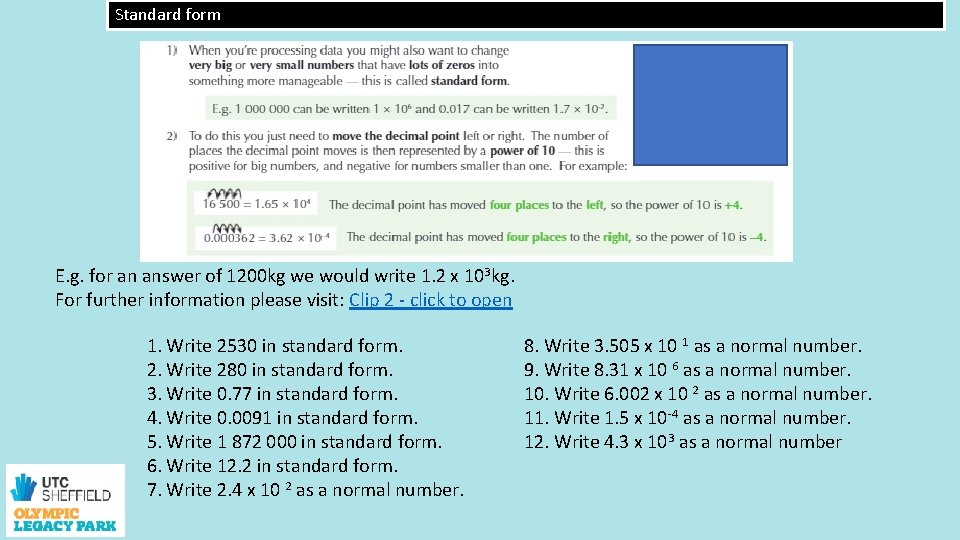
Standard form E. g. for an answer of 1200 kg we would write 1. 2 x 103 kg. For further information please visit: Clip 2 - click to open 1. Write 2530 in standard form. 2. Write 280 in standard form. 3. Write 0. 77 in standard form. 4. Write 0. 0091 in standard form. 5. Write 1 872 000 in standard form. 6. Write 12. 2 in standard form. 7. Write 2. 4 x 10 2 as a normal number. 8. Write 3. 505 x 10 1 as a normal number. 9. Write 8. 31 x 10 6 as a normal number. 10. Write 6. 002 x 10 2 as a normal number. 11. Write 1. 5 x 10 -4 as a normal number. 12. Write 4. 3 x 103 as a normal number

Rearranging equations This is something you will have done at GCSE and it is crucial you master it for success at A level. For a recap of GCSE watch the following links: Clip 3 - click to open Clip 4 - click to open Task: Rearrange the following: 1. E=m x g x h to find h 2. Q= I x t to find I 3. E = ½ m v 2 to find m 4. E = ½ m v 2 to find v 5. v = u + at to find u 6. v = u + at to find a 7. v 2 = u 2 +2 as to find s 8. v 2 = u 2 +2 as to find u

Significant figures Task 1: Give the following to 3 significant figures: 1. 3. 4527 2. 40. 691 3. 0. 838991 4. 1. 0247 Task 2 Calculate the following to a suitable number of significant figures: 1. 63. 2 ÷ 78. 1 = 2. 39 + 78 + 120 = 3. (3. 4+3. 7+3. 2) ÷ 3 = 4. 0. 0256 x 0. 129 =

Week 1 session 2 Identifying SI units and use these units to check homogeneity of equations units

The SI system of units There are seven fundamental base units which are clearly defined and on which all other derived units are based: Clip 5 - click to open You need to know these

SI Base Units Quantity Unit distance meter time second current ampere temperature kelvin quantity of substance mole luminous intensity candela mass kilogram Notice : No Newton or Coulomb

Derived units Other physical quantities have units that are combinations of the fundamental units. Speed = distance/time = ms-1 Acceleration = ms-2 Force = mass x acceleration = kgms-2 (called a Newton) (note we can write ms-1 rather than m/s)

Some important derived units 1 N = kg. m. s-2 1 J = kg. m 2. s-2 1 W = kg. m 2. s-3 (F = ma) (W = Force x distance) (Power = energy/time)

Temperature. • To convert from 0 C to Kelvin (the SI unit) you need to add 273 • E. g. 200 C is 293 K • If you are measuring change in temperature you do not need to convert the units as 10 C change is the same as 1 K

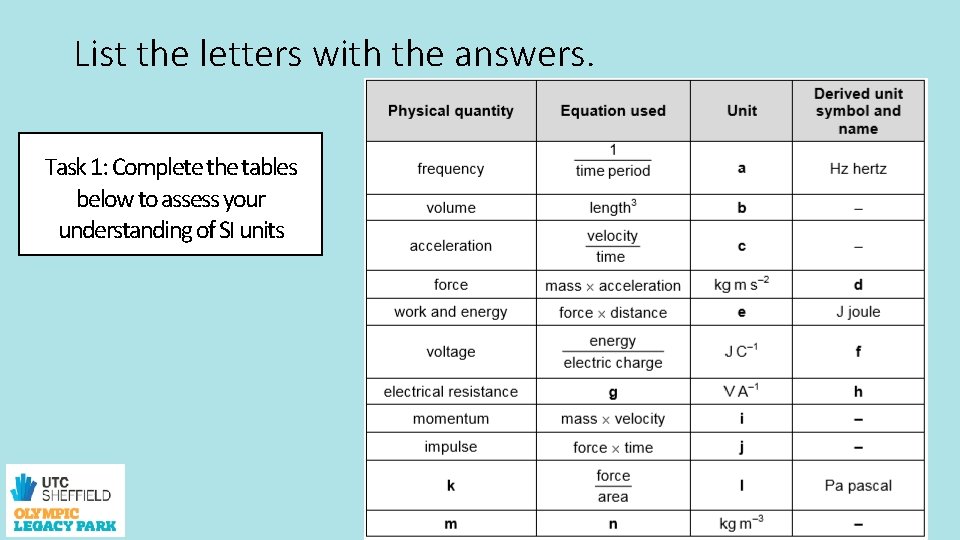
List the letters with the answers. Task 1: Complete the tables below to assess your understanding of SI units

Homogeneity of physics equations • This is a way to check equations and uses the SI units • You write down the SI units on the right hand side • Write the SI units for the left hand side and resolve them • And then check that the right and left hand side are the same. Clip 6 - click to open

Homogeneity of physics equations • Worked example Question Check that the equation: kinetic energy = ½ m v 2 is homogeneous.

Homogeneity of physics equations Answer • Make sure you always state which side of the equation you are working on, left-hand side (LHS) or right-hand side (RHS). • Step 1 Start with the LHS. The unit of kinetic energy is the joule. Change this to base units. LHS: J = N m = kg m s– 2 × m = kg m 2 s– 2 • Step 2 Repeat Step 1 for the RHS: units of 1/2 m v 2 are kg × (m s– 1)2 = kg m 2 s– 2 (The constant, ½ , is a number with no units. ) • Step 3 Don’t forget to write your conclusion. LHS = RHS so the equation is homogeneous. • We can’t tell that there is a ½ in the equation, so we cannot say that the equation is correct, only that it is homogeneous.

Homogeneity of physics equations Task 1: Complete the questions below to assess your understanding of homogeneity of physics equations. Homogeneity of physics equations 1. Use base units to show the equation Q = I t for electric charge passing a point in time t, when the electric current is I, is homogeneous. 2. Use base units to show that the equation P = I V is homogeneous, where I is electric current, V is voltage, and P is power measured in watts (W). (Hint: 1 W = 1 J s– 1) 3. The Earth’s gravitational field strength, g = 9. 81 N kg– 1, is also sometimes given as the acceleration due to gravity, g = 9. 81 m s– 2. Show that these units are equivalent.

Week 2 session 1 Motion graphs and circular motion introduction.

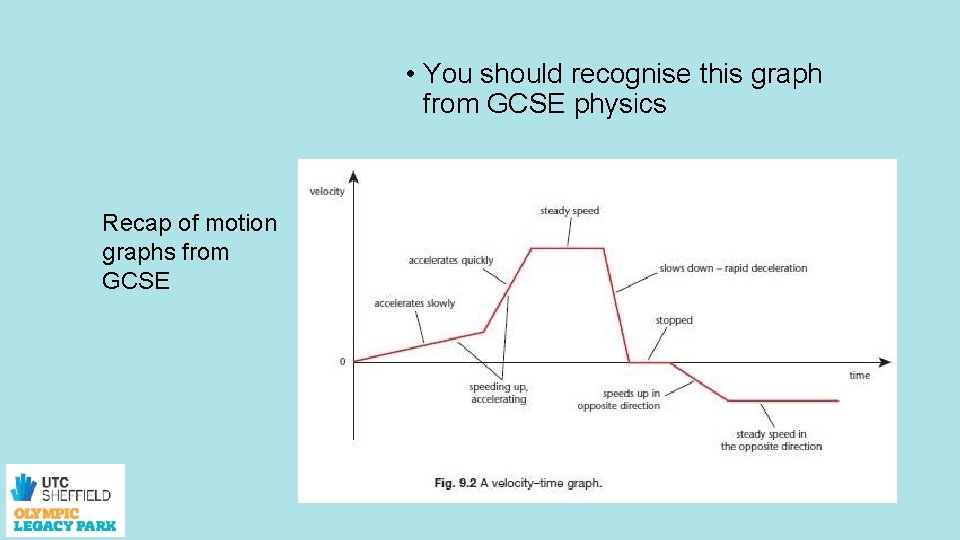
• You should recognise this graph from GCSE physics Recap of motion graphs from GCSE

Displacement time graphs Distance or displacement These are used to denote 2 directions as in going to and from a start point or a ball thrown in the air and returning. Also displacement is the straight line from start to end point.

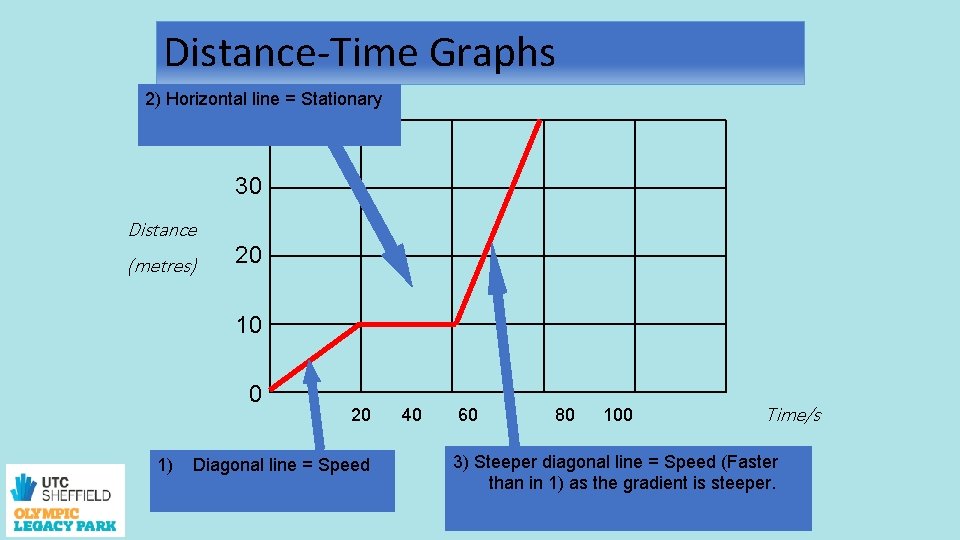
Distance-Time Graphs 2) Horizontal line = Stationary 40 30 Distance (metres) 20 10 0 1) 20 Diagonal line = Speed 40 60 80 100 Time/s 3) Steeper diagonal line = Speed (Faster than in 1) as the gradient is steeper.

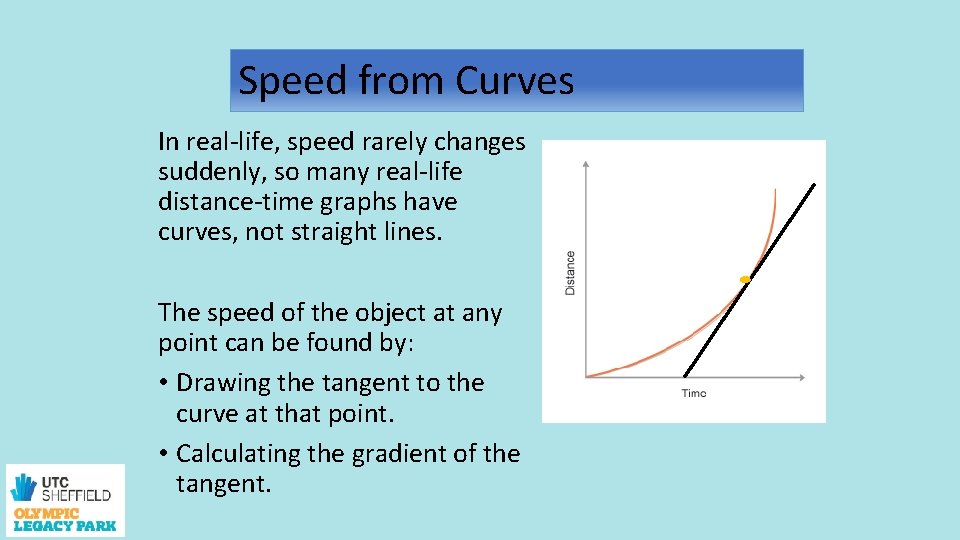
Speed from Curves In real-life, speed rarely changes suddenly, so many real-life distance-time graphs have curves, not straight lines. The speed of the object at any point can be found by: • Drawing the tangent to the curve at that point. • Calculating the gradient of the tangent.

Velocity and speed? • When moving in straight lines there is little difference. It is only when direction changes that velocity changes become more important, e. g. you can travel at 20 m/s in a circle with constant speed but the velocity cannot be constant as the direction of movement is changing!

Going in circles!!! • One difference between A level and GCSE physics is circular motion.

Speed. • At constant speed, v, in a straight line, • v = s/t where s is distance travelled and t is time • In a circle of radius r and T is the time to move once around the circumference. • The equation for speed is • v = 2πr T Clip 7 - click to open Clip 8 - click to open

Circular motion. Task : Complete the problems below Problem 1: • During their physics field trip to the amusement park, Tyler and Maria took a rider on the Whirligig. The Whirligig ride consists of long swings which spin in a circle at relatively high speeds. As part of their lab, Tyler and Maria estimate that the riders travel through a circle with a radius of 6. 5 m and make one turn every 5. 8 seconds. Determine the speed of the riders on the Whirligig. Problem 2: • The tallest Ferris wheel in the world is located in Singapore. Standing 42 stories high and holding as many as 780 passengers, the Ferris wheel has a diameter of 150 meters and takes approximately 30 minutes to make a full circle. Determine the speed of riders (in m/s) on the Singapore Flyer. Problem 3: • During the spin cycle of a washing machine, the clothes stick to the outer wall of the barrel as it spins at a rate as high as 1800 revolutions per minute. The radius of the barrel is 26 cm. Determine the speed of the clothes (in m/s) which are located on the wall of the spin barrel. Problem 4: • Elmira, New York boasts of having the fastest carousel ride in the world. The merrygo-round at Eldridge Park takes riders on a spin at 8. 0 m/s. The radius of the circle about which the outside riders move is approximately 7. 4 m. Determine the time for outside riders to make one complete circle.

Week 2 session 2 Equations of motion.

Equations of Motion • These are equations which can be used whenever an object travels with constant, uniform acceleration in a straight line. • We write these equations using 5 symbols: s, u, v, a, t. • Suppose an object is travelling at a velocity u and then moves with a uniform acceleration a for a time t. • Its velocity is then v and it has travelled a distance s. Clip 9 - click to open

Equations of Motion • In questions, ‘initially at rest’ means u = 0. • A negative number for the acceleration means the object is slowing down (decelerating) v = u + at s = ½(u+v)t s = ut + ½at 2

Equations of Motion Task 1: Complete the problems below 1. A car is travelling along a straight road at 8. 0 m s-1. It accelerates at 1. 0 m s-2 for a distance of 18 m. How fast is it then travelling? 2. A car is initially stationary. It has a constant acceleration of 2. 0 m s-2. 1. Calculate the velocity of the car after 10 s. 2. Calculate the distance travelled by the car at the end of 10 s. 3. A train accelerates steadily from 4. 0 ms-1 to 20 m s 1 in 100 s. 1. Calculate the acceleration of the train. 2. From its initial and final velocities, calculate the average velocity of the train. 3. Calculate the distance travelled by the train in this time of 100 s.

Task 2: practical skills Calculating gravity experimentally. • Plan an experiment to measure the acceleration of a 20 cm long piece of heavy card to pass through a light gate connected to a data logger. • This is a planning exercise only. • Draw a diagram of the experimental arrangement to be used. Show clearly on your diagram the distance the card falls. • List any precautions that should be taken to minimise risk. • Explain how the computer can be programmed to calculate the average velocity of the card as it passes through the light gate. • Show the equation v 2 = u 2 + 2 as can be rearranged and used to calculate the acceleration.

Week 3 session 1 Series and parallel circuits Potential difference, Current and resistance

GCSE recap TASK • On the next slide is an outline for a mind map on electricity. Use this as the basis for your own revision mind map of electricity include as much detail as you can, stretch each concept as close to A level standard as you can.

Week 3 session 2 Series and parallel circuits Potential difference, Current and resistance

Circuits Open the link to test your knowledge of circuit symbols task 1 - click to open

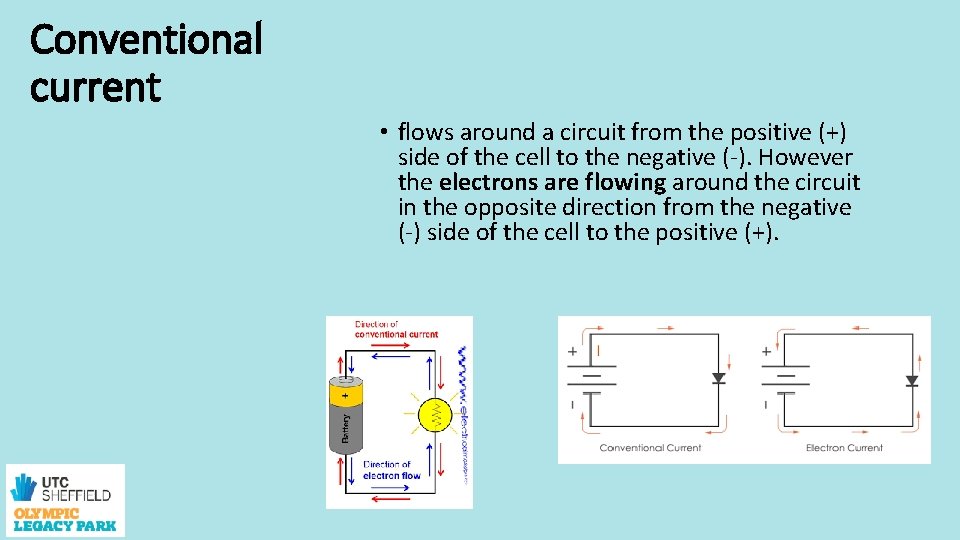
Conventional current • flows around a circuit from the positive (+) side of the cell to the negative (-). However the electrons are flowing around the circuit in the opposite direction from the negative (-) side of the cell to the positive (+).

The big difference between GCSE and A level is the equations are represented by letters, not always obvious ones e. g. Charge (Q) – charge is measured in coulombs (C). charge is represented by Q!!! A single electron carries a charge of 1. 6 x 10 -19 C. Circuits equations! Charge, Current & Potential Difference Clip 10 - click to open Current (I) – is measured in amperes (A). Current is the rate of flow of charge. A current of 1 A means that 1 coulomb of charge flows past a point in a circuit every second. ( 1 A = 1 C s-1 ) Current is measured in a circuit using an ammeter which is placed in series with the component of interest in the circuit. I = current in amperes, A DQ = charge in coulombs, C Dt = time in seconds, s Potential difference (V) – is measured in volts (V). Potential difference is the work done per unit charge. A potential difference of 1 V means that 1 joule of work is done per coulomb of charge. ( 1 V = 1 J C-1) Potential difference in a circuit is measured using a voltmeter which is placed in parallel with the component of interest in the circuit. V = potential difference in volts, V W = work done or energy transferred in joules, J Q = charge in coulombs, C Resistance (W) – is the ratio of potential difference across a component to the current flowing through it, it is measure in ohms (W). R = resistance in ohm’s, W V = potential difference in volts, V I = current in amperes, A

Electrical power • You will already be familiar with the idea of electrical power being the rate of electrical work done, or the rate of energy transfer by electric charges. You should also know the definitions: The potential difference (p. d. ) is the work done per unit charge, V = W ÷ Q The intensity of the electric current is the charge transferred per unit time, =Q÷t I • Multiplying these two quantities eliminates the charge, leaving you with work done per unit time, which is the electrical power: • V I = (E ÷ Q) × (Q ÷ t) = E ÷ t = P • The definition of resistance, R = V ÷ I can be used to eliminate either V or I from the expression. So: • P = V I = V 2 ÷ R = I 2 R • If you use volts (V) as the p. d. unit, amperes (A) as the current unit and ohms (Ω) for the resistance unit then the unit for power will be watts (W), as you should expect.

Electrical power questions Task 2 : Complete the problems

Week 4 session 1 Force on a wire carrying current when in a magnetic field.

Magnetic field lines Magnetic fields go from north pole to south pole on permanent magnets. There also magnetic fields around wires that are carrying a current. The diagram shows how you can work out the direction of the field around a wire these interact in a coil and look similar to a bar magnet. clip 11 -click to open

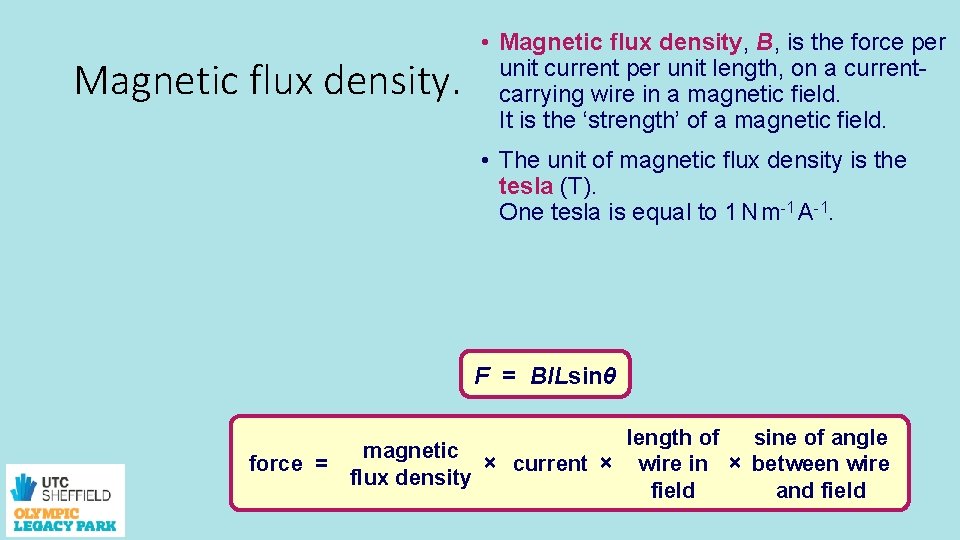
Magnetic flux density. • Magnetic flux density, B, is the force per unit current per unit length, on a currentcarrying wire in a magnetic field. It is the ‘strength’ of a magnetic field. • The unit of magnetic flux density is the tesla (T). One tesla is equal to 1 N m-1 A-1. F = BILsinθ force = magnetic × current × flux density length of sine of angle wire in × between wire field and field

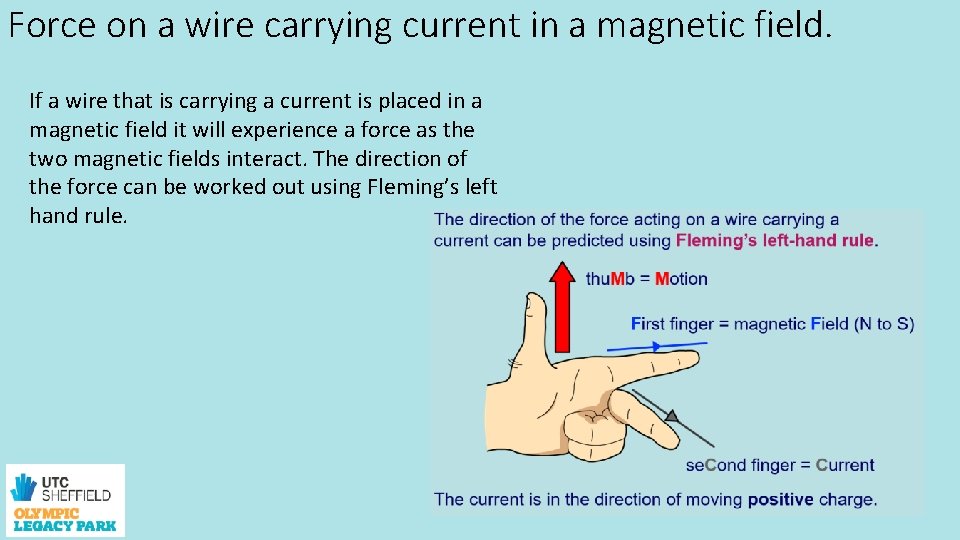
Force on a wire carrying current in a magnetic field. If a wire that is carrying a current is placed in a magnetic field it will experience a force as the two magnetic fields interact. The direction of the force can be worked out using Fleming’s left hand rule.

Force on a wire carrying current in a magnetic field. Task 1 label this diagram, you must include conventional current, force, magnetic field and units. Task 2 plan an experiment to show the effect of increasing the current on the force the wire experiences. Include what the independent variable is and you will change it, dependant variable (hint remember the difference between units for mass and weight), and control variables. Don’t forget any safety considerations. clip 12 -click to open

Week 4 session 2 work done and force

Work done • You will remember the equation from GCSE • Work done = force X distance • Work in Joules J • Force in Newtons N • Distance in meters m • But what if the force is at an angle to the distance travelled ? ? ?

Work done • We use Pythagoras to help • now the equation is… • Work done = force x cos Ø x distance clip 13 - click to open

Task complete the calculations Work done 1. Calculate the work done when: a) The resultant force on a car is 22 k. N and it travels 2. 0 km. (1 mark) b) A skier of weight 620 N skis for 150 m down a slope at 80 o to the vertical. (1 mark) c) A passenger pulls a suitcase across a horizontal floor, with a force of 160 N at an angle of 35º to the horizontal, to the check-in desk 55 m away along the floor. (1 mark) 2. Calculate the work done when a weightlifter lifts a weight of 200 kg to a height 1. 8 m above the ground. 3. Figure 1 shows a plan view of a shopping trolley. It is being pushed forwards at constant speed with a force of 25 N, against friction, but it is moving sideways at an angle of 30º and travels 5. 0 m in this direction. Calculate the work done on the trolley by the pushing force. • Figure 1

Week 5 session 1 Longitudinal and transverse waves. Properties of Waves and behaviour

Waves GCSE recap. • A wave is a periodic disturbance in a material (medium) or space. • Each particle of the medium vibrates, or oscillates, about a fixed position. Energy is transferred outwards from the source of the wave. • Waves that move outwards from their source are called progressive (travelling) waves. The two types of progressive wave are transverse and longitudinal.

2 types of wave. • In transverse waves, each particle oscillates perpendicular to the direction of propagation of the wave. There is no horizontal movement. • In longitudinal waves, each particle oscillates parallel to the direction of propagation of the wave. There is no vertical movement. clip 14 -click to open

Reflection refraction and diffraction • Reflection is where the wave rebounds off the surface. • Refraction is when the wave changes velocity (speed and usually direction). • Diffraction occurs when a wave encounters an obstacle or a slit. It is defined as the bending of waves around the corners of an obstacle.

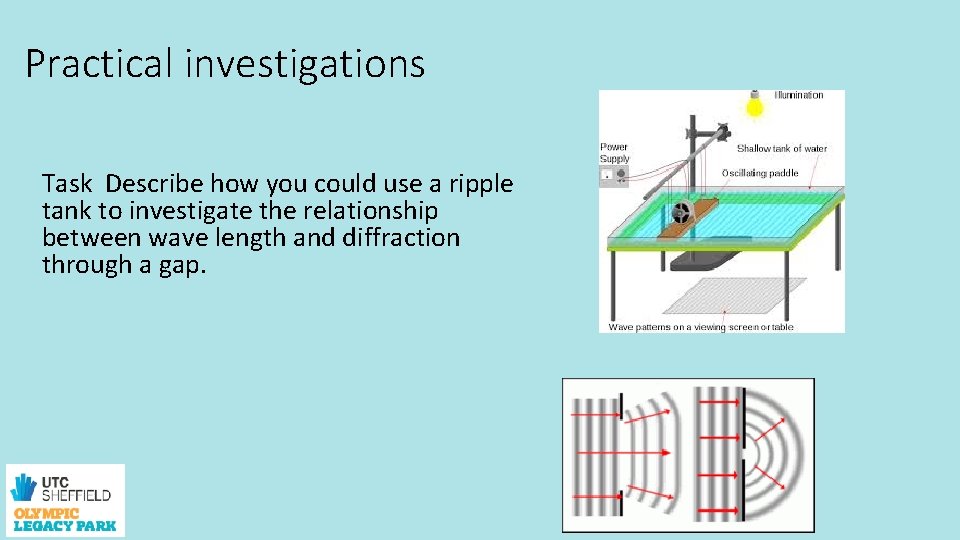
Practical investigations Task Describe how you could use a ripple tank to investigate the relationship between wave length and diffraction through a gap.

Week 5 session 2 Structure of the atom Types of ionising radiation

Radioactivity • Particles emit radiation from the nucleus when they are unstable, e. g. an isotope with more neutrons than a regular atom may be unstable.

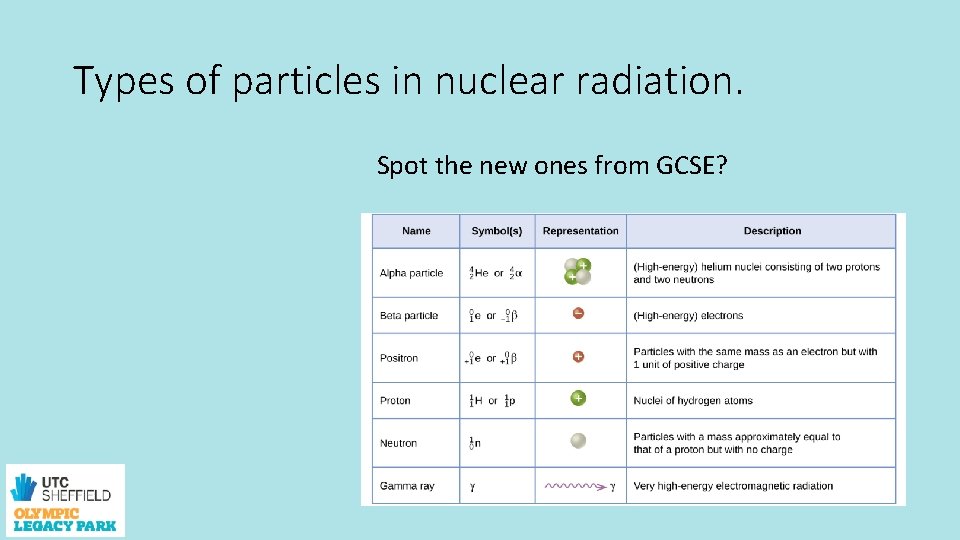
Types of particles in nuclear radiation. Spot the new ones from GCSE?

ATOMS • What’s in an atom? • Protons neutrons and electrons. • But at A level it gets more interesting. • Watch the clips on the link below. clip 15 - click to open

Sub atomic particles. Task Research and produce a Power. Point summarising, the new subatomic particles you may encounter at A Level, what are they how were they discovered and by who, what do they do? • Quarks • Baryons • Mesons • Leptons