A Language for Mathematical Knowledge Management Steve Kieffer

A Language for Mathematical Knowledge Management Steve Kieffer Carnegie Mellon University

What is Mathematical Knowledge? l l l 2 Theorems Definitions Proofs

How do we “manage” it? l l l 3 Experts Books Wikipedia?

Idea for MKM: Encyclopedia Entries, Stored in Computers 4

How transparent is the entry, to the computer? 5

What do we want to do with mathematical knowledge? l l l 6 Learn it Add to it Study its history Formally verify it Study its logical structure. . .

My Work l l l 7 1. Parser 2. Database of definitions 3. Translator 4. Statistics on logical structure 5. GUI for concept exploration

Choice of Language 8

Choice of Language 9

Mizar 10

LPT l l 11 Designed by Friedman Adds nice features to language of set theory

Terms in LPT Ordered tuples: 12

Terms in LPT Function evaluation: 13

Terms in LPT Infix functions: 14

Terms in LPT Sets: 15

Terms in LPT Descriptions: 16

Terms in LPT Lambda abstraction: 17

Formulas in LPT Predication: 18

Formulas in LPT Infix relations: 19

Formulas in LPT Quantifiers: 20

R is a partial order on A 21

R is a partial order on A 22

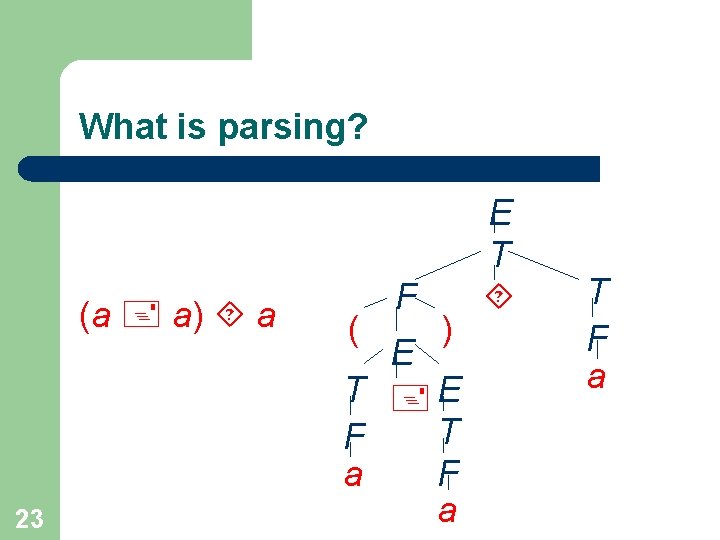
What is parsing? (a a) a 23 ( F ) E T F a E T T F a

[[[([[[a]F]T]E]E)]F [[a]F]T]T]E ( 24 F ) E T F a E T T F a

[ [[ 25 ] [[ ] [ ] FCN] [ [f ]] [f ]= { < [x ][ , y] > : rel’n var formula var var tuple var ] ]] f ( x ) = [y ] } var formula term formula

Parsing method l l l 26 Earley algorithm n 3 runtime parses any context free grammar

Simple example E Grammar: E T E E T T F F (E) F a Input: (a a) a 27 T F ( T F a E ) E T F a

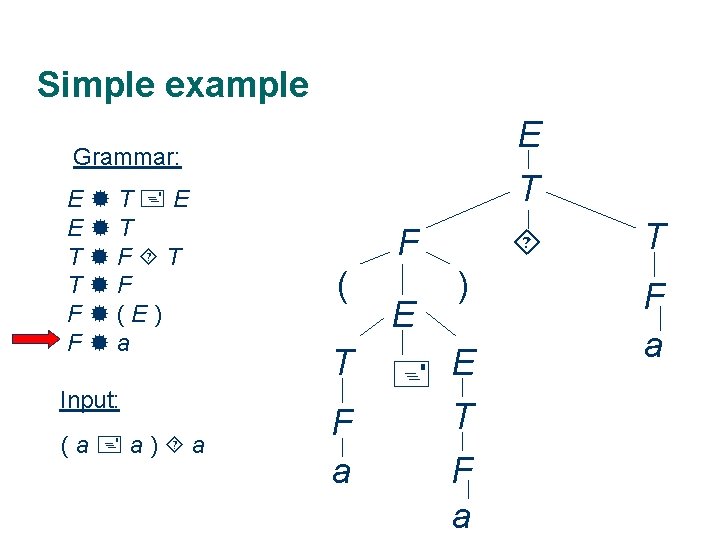
Earley algorithm Grammar: (1) (2) (3) (4) (5) (6) E T E E T T F F (E) F a Input: (a a) a 28 I 0 I 1 I 2 [E T E, 0] [E T, 0] [T F, 0] [F (E), 0] [F a, 0] [F ( E), 0] [E T E, 1] [E T, 1] [T F, 1] [F (E), 1] [F a, 1] [F a , 1] [T F T, 1] [T F , 1] [E T E, 1] [E T , 1] [F (E ), 0] I 3 I 4 I 5 [E T E, 1] [E T E, 3] [E T, 3] [T F, 3] [F (E), 3] [F a, 3] [F a , 3] [T F T, 3] [T F , 3] [E T E, 3] [E T E , 1] [F (E ), 0] [F (E) , 0] [T F T, 0] [T F , 0] [E T E, 0] [E T , 0] I 6 I 7 [T F T, 0] [T F T, 6] [T F, 6] [F (E), 6] [F a, 6] [F a , 6] [T F T, 6] [T F T , 0] [E T E, 0] [E T , 0] 64642156432

My Work l l l 29 1. Parser 2. Database of definitions 3. Translator 4. Statistics on logical structure 5. GUI for concept exploration

Translation l l 30 LPT as language for proof system? Set up translation to make database useable. Database has set-theoretic foundational definitions (e. g. von Neumann ordinals). Translate into DZFC (“Definitional ZFC”), a conservative extension of ZFC.

Comparison: LPT vs. DZFC 31

Comparison: LPT vs. DZFC 32

Comparison: LPT vs. DZFC 33

My Work l l l 34 1. Parser 2. Database of definitions 3. Translator 4. Statistics on logical structure 5. GUI for concept exploration

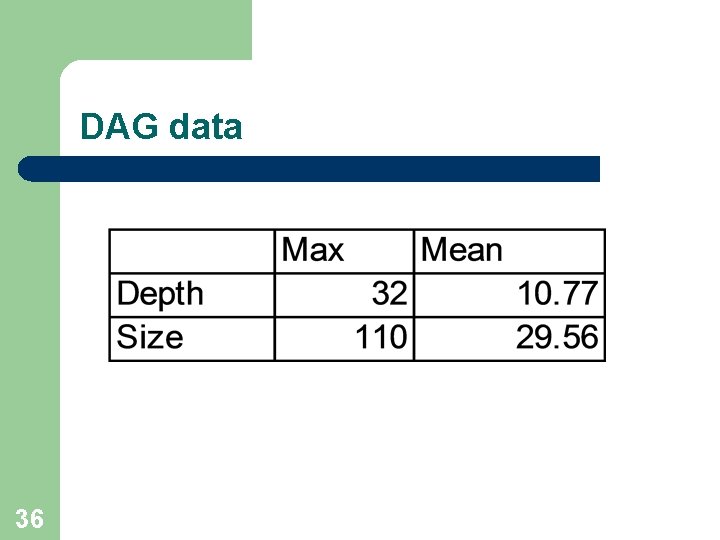
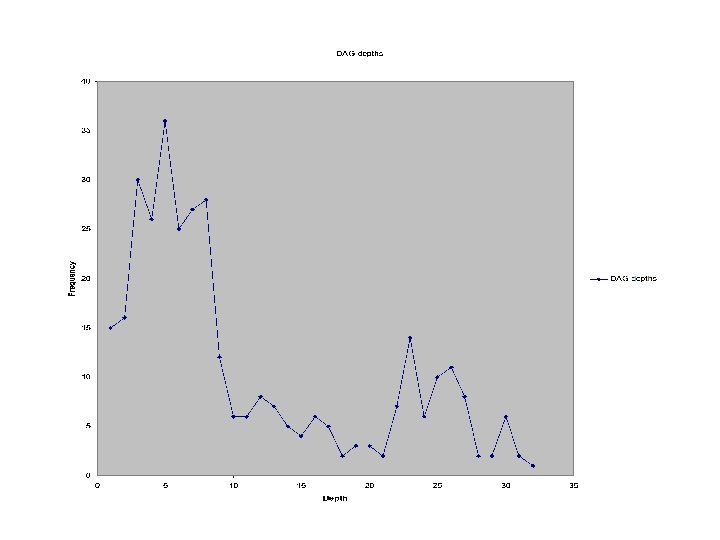
Directed Acyclic Graph (DAG) of Conceptual Dependencies Depth: 4 35 Size: 5

DAG data 36

37

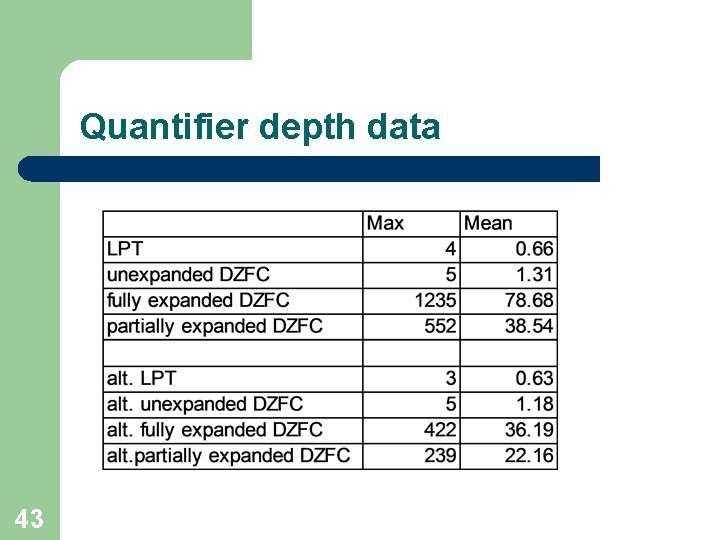
Quantifier depth: alternating or nonalternating 38

Expanding formulas Definitional axiom for PORD in DZFC: Definiens for PORD: To expand, locate the definiens for each defined concept appearing above. : : : 39 Then plug in.

Expanding formulas The result: 40

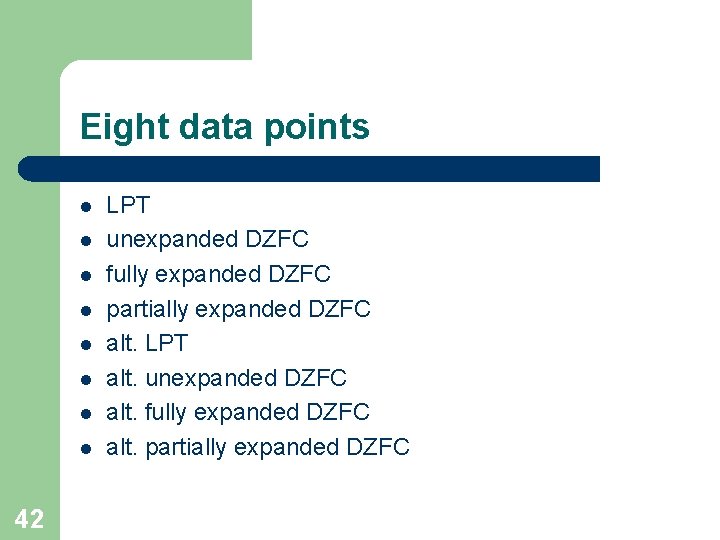
Three expansion levels l l l 41 1. No expansion 2. Total expansion 3. Partial – lowest foundational concepts left unexpanded

Eight data points l l l l 42 LPT unexpanded DZFC fully expanded DZFC partially expanded DZFC alt. LPT alt. unexpanded DZFC alt. fully expanded DZFC alt. partially expanded DZFC

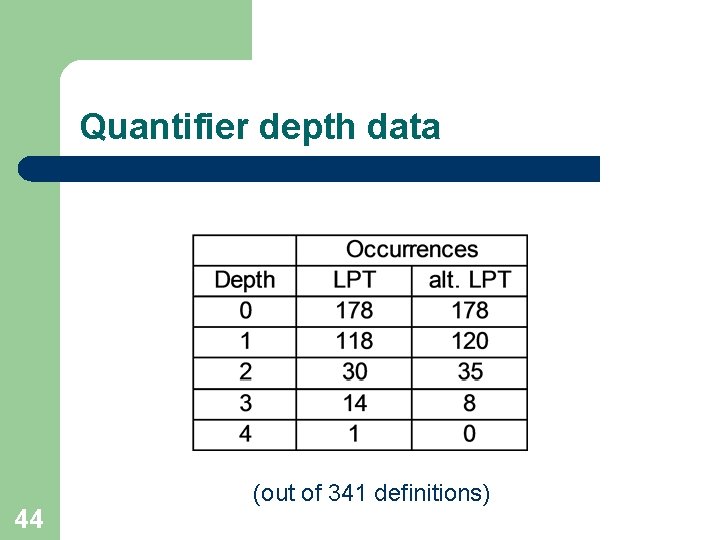
Quantifier depth data 43

Quantifier depth data 44 (out of 341 definitions)

My Work l l l 45 1. Parser 2. Database of definitions 3. Translator 4. Statistics on logical structure 5. GUI for concept exploration

Summary l l l 46 1. Parser 2. Database of definitions 3. Translator 4. Statistics on logical structure 5. GUI for concept exploration