A Laboratory Test of the Equivalence Principle as

A Laboratory Test of the Equivalence Principle as Prolog to a Spaceborne Experiment Robert D. Reasenberg and James D. Phillips Smithsonian Astrophysical Observatory Harvard-Smithsonian Center for Astrophysics 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 1

Motivation for Testing the Equivalence Principle can be found at this conference. • Central to the present accepted theory of gravity. – Some theorists argue it is the place to look for a breakdown of general relativity. • The evidence that leads to dark energy may be telling us that we need a new gravity theory. • Attempts to create a quantum theory of gravity show a failure of the equivalence principle. • Gravity is the least well tested force. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 2
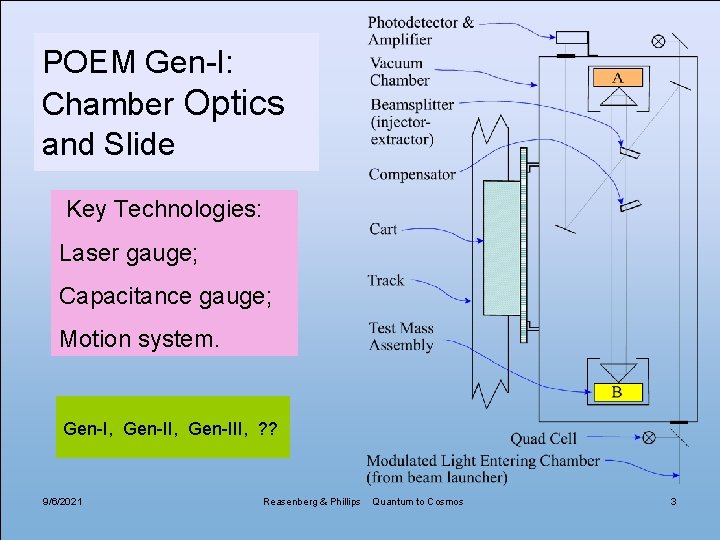
POEM Gen-I: Chamber Optics and Slide Key Technologies: Laser gauge; Capacitance gauge; Motion system. Gen-I, Gen-III, ? ? 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 3

Gen-I TMA Φ = 44. 5 mm h = 36. 5 mm 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 4

A Vacuum Chamber in Free Fall? • Advantages – No mechanisms or motors in vacuum or power shafts passing through the wall to operate on each toss, at high speed and at sub-mm accuracy. • Laser gauge and capacitance gauge components must move with the TMA. – Chamber is relatively small. • Disadvantages – Massive object (ca. 50 kg) moves at up to 5 m/s, but must have low vibration level and rapid change of direction. – A vacuum pump must ride with chamber. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 5

Second Pair of TMA, Gen-II • Cancellation of gravity gradient. • Δg / g = 1. 6 10 -7 (for Δh = 0. 5 m) A B – Local sources vary. • Requires absolute distance. – dg/dz = 3 10 -7 g / m. – TMA is 30% test mass. – Science goal (Gen-III): σ (Δg) / g = 5 × 10 -14 – Measurement goal = 1. 5 10 -14 => Δh-error < 0. 05 μm. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos B A 6

Interchanges, Gen-III • Gen-III goal: σ (Δg) / g = 5 × 10 -14 – Requires control of systematic error. • Gen-III introduces interchanges to cancel systematic errors. – Robotic left-right. • Perhaps every 10 minutes. – Manual top-bottom. • Requires braking vacuum => separate runs 1 or 2 days apart. – Manual interchange of test substance between TMA. • One interchange per experiment – if needed. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 7

Principal Systematic Error Sources, I • Earth’s gravity gradient. – Absolute distance measurement. – Top-bottom interchange. – Second pair of TMA. • Coriolis force and transverse velocity. – Capacitance gauge measures velocity. – Air slide reduces vibration => reduced transverse velocity. • Gravity gradient due to local mass (parked cars). – Second pair of TMA. – Frequent left-right interchanges of TMA. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 8

Principal Systematic Error Sources, II • Rotation of TMA around horizontal axis. – Measured with capacitance gauge and calibrated by inducing fast rotation with high voltage on capacitance gauge electrodes. • Misalignment of measurement beam WRT cavity. – Measure beam position. – Measured TMA position with capacitance gauge. – Measure effect by exaggerated beam tilt. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 9

Why the Tracking Frequency Laser Gauge? No other laser gauge will do. • When we started working on POINTS, there was no adequate laser gauge. – We needed 2 pm in 1 minute to 1 hour. – We found only one serious contender, the standard heterodyne gauge. • For POEM, we need 1 pm in 1 s. – We would like 0. 1 pm in 1 s! – We also need absolute distance to 0. 01 μm (differential, averaged over an experiment) 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 10
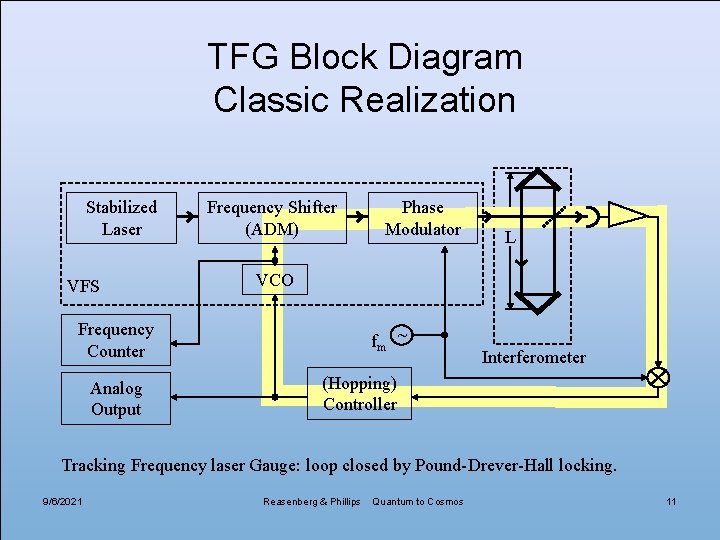
TFG Block Diagram Classic Realization Stabilized Laser VFS Frequency Shifter (ADM) L VCO Frequency Counter Analog Output Phase Modulator fm ~ Interferometer (Hopping) Controller Tracking Frequency laser Gauge: loop closed by Pound-Drever-Hall locking. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 11

4 TFG Advantages • Intrinsically free of the cyclic bias characteristic of heterodyne laser gauges. • Able to operate in a cavity for increased sensitivity. • Absolute distance available at little additional cost. • Able to suppress polarization errors (nm scale or much smaller with a cat’s eye) and, when used in a cavity, to suppress alignment errors. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 12

TFG Precision • Shot noise limit, He. Ne power of 1 μW, 1 s. – Michelson intrinsic precision: 0. 06 pm. – Similar for heterodyne gauge. • Current TFG limitation is “technical noise. ” – σ < 10 pm on 0. 1 s samples. (12/02). 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 13

TFG Absolute Distance • Fringe spacing in optical frequency, Φ = c/(2 L). • Measure Φ, get L with no ambiguity length. – Measure optical frequency before and after a hop of K fringes to get ΔF. K>1 increases precision. – L = K c / (2 ΔF) • Precision degraded by η = ΔF / F. • Either use two lasers to read simultaneously or hop fast to avoid errors due to fluctuating path. – TFG does hop fast (50 k. Hz demonstrated), unlike most narrow-linewidth laser systems. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 14

How Large Can η Be? • Using He. Ne & an ADM, 500 MHz / 470 THz = 10 -6. • Using a semiconductor laser, the frequency counter limit yields 2 GHz / 200 THz = 10 -5. – This yields wave count => connect to phase measurement. • Using a series of markers. – Assume the DFB laser we are using. – 60 GHz / 200 THz = 3 10 -4. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 15

Coriolis • Coriolis acceleration. – Vertical Coriolis acceleration: ac = 2 ve-w |ω| cos(latitude). – Earth rotation: |ω| = 7. 292 10 -5 /s. – Require ve-w be measured to 33 nm/s [bias < 0. 25 nm/s]. • Add capacitance gauge. – Collaboration with W. Hill (Rowland Institute at Harvard). – 5 degrees of freedom for each of 4 TMA. – TMA free floating and minimal drive signal. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 16
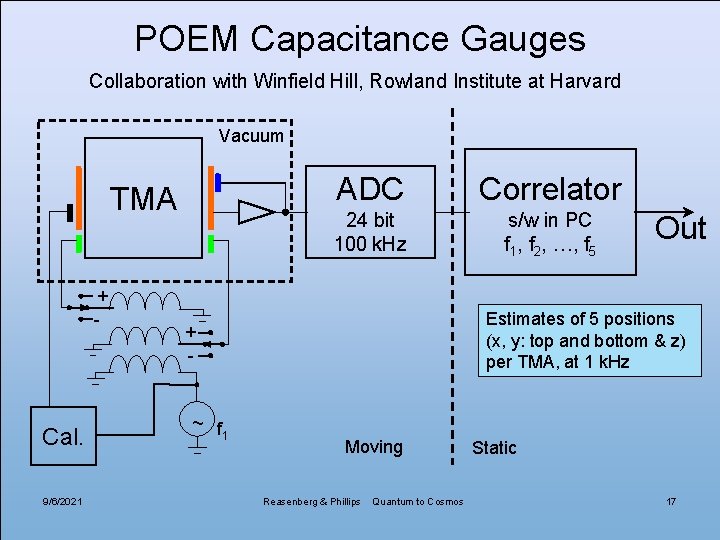
POEM Capacitance Gauges Collaboration with Winfield Hill, Rowland Institute at Harvard Vacuum TMA + - Cal. 9/6/2021 ADC Correlator 24 bit 100 k. Hz s/w in PC f 1, f 2, …, f 5 Estimates of 5 positions (x, y: top and bottom & z) per TMA, at 1 k. Hz + - ~ f 1 Out Moving Reasenberg & Phillips Quantum to Cosmos Static 17

9/6/2021 Drive: 0. 1 V rms, 10 – 20 k. Hz Sensitivity: < 8 nm @ 1 s. Electrode gaps: 1 mm (nominal) Reasenberg & Phillips Quantum to Cosmos 18

Motion System • Slide (commercial now). – Follow nominal trajectory. – Low vibration motion. • Torsion bar bouncer. – Store and return energy. – Do no harm. (Cause no shock. ) • Horizontal cable hit by moving system. – Soft onset of force on moving system, from geometry. – Effective mass of cable, 0. 05 kg (chamber, 40 kg). 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 19

Torsion Bar Bouncer • Torsion bar with lever holds each end of cable. – Bar working size, 74 x 1 inch. – 4340 steel, heat treated. (Racing car industry) – Made possible by moving-chamber approach • Internal modes of torsion bar (cf. coil springs). – F > 1 k. Hz. – Small moment of inertia (vs Mchamber Rlever 2). • Status: working well – alone and with motor. – Replaces system with ¼ inch cable running over pulleys. This had too much friction. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 20

Present Slide • Anorad slide including linear motor, Renishaw gauge, and track rollers running on small rails. • TMA must be launched vertically. • Vibration at micron level (mostly 100 – 200 Hz). – Transverse velocity 3 mm / s • Long-standing plan: Use air-bearing slide. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 21

Laser Gauge : Progress & Status • He. Ne TFG works in moving system. • Two-channel frequency counter built. – Contiguous measurements – no dead time. – Precise synchronization. (Jim Mac. Arthur, Harvard-Physics Electronics Shop) • Developing TFG using semiconductor lasers. – – 9/6/2021 DFB lasers at 1550 nm communications band. Lasers locked to reference cavity. Improved electronics being developed by contractor. On path to space-based application. Reasenberg & Phillips Quantum to Cosmos 22

Capacitance Gauge: Progress & Status • Architecture long established. • Electrode assemblies in hand – preliminary version. • All electronic components designed and in various stages of fabrication at Rowland Institute. – Packaging to be finalized soon. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 23

Motion System: Progress & Status • Torsion-bar bouncer has high mechanical efficiency. – Motor servo can be (and has been) tuned less aggressively =>lower noise yet still follows trajectory to 10 s of μm. • Vibration measured in present slide – too high. • Next step, air-bearing slide to replace wheels and track (as long planned). – – 9/6/2021 Use granite beam and porous graphite bearings. Preliminary designs completed – no serious problems. Found vendors: meet requirements at reasonable price. Have hardware to make clean dry compressed air. Reasenberg & Phillips Quantum to Cosmos 24

POEM Summary • The SAO Principle of Equivalence Measurement is a Galilean test of the WEP. • The goal for the Gen-III version of the experiment is σ (Δg) / g = 5 × 10 -14 for several pairs of substances. • All Gen-I components are working and being tuned or modified for better performance; some components, originally described as part of Gen-II, are started. – Capacitance gauge (nearly finished). – Air slide (preliminary design). • The measurement system is being designed both for the control of systematic error and, where applicable, to be easily translated to be space-based. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 25

More Information • www. cfa. harvard. edu/poem • reasenberg@cfa. harvard. edu • 617 -495 -7108 • jphillips@cfa. harvard. edu • 617 -495 -7360 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 26

Principal Approaches Today • Torsion balance tests. – Sensitive to sun's gravity or horizontal component of earth's gravity. Also, other distant matter. – Best results: σ (Δg) / g = 4 × 10 -13. • Adelberger et al. 2001. (confusion about factor of 3) • Galilean tests (dropping). – Sensitive to full vertical gravity of earth. – Niebauer et al. (Faller) 1987, σ (Δg) / g = 5 × 10 -10. – Best results: σ (Δg) / g = 10 -10 (Dittus 2001, 109 m tower, σ (Δg) / g = 10 -12, projected). – Works (better) in space: our long-term goal. – POEM (σ (Δg) / g = 5 × 10 -14, projected) 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 27

Heterodyne Gauge • Cyclic bias due to polarization leakage. – Multiple averaging reduces bias to 0. 15 pm in few min. [Gursel, SPIE 2200, pp. 27 -34, 1994]. – Abandoned by SIM in favor of concentric beams. – Variant without polarization: 3 pm in 1 sec. [Gursel, priv. comm. 2002]. • Absolute distance possible. – Requires either a second laser or a tunable laser. • Complexity. • Not able to operate in a cavity. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 28
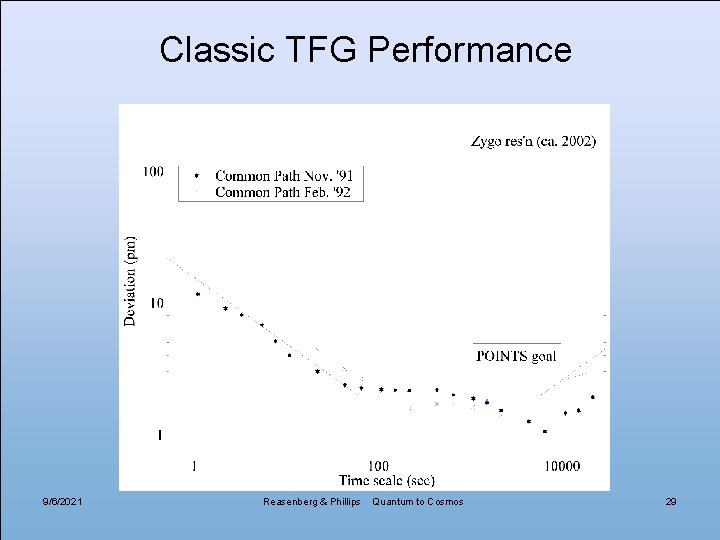
Classic TFG Performance 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 29

POEM Smooth Motion Problem • Coriolis acceleration. – Require ve-w be measured to 33 nm/s [bias < 0. 25 nm/s]. • Capacitance gauge. – Dynamic range limit: 4 104. (engineering judgment) • Maximum transverse velocity for TMA. – (0. 25 nm/s) (4 104) = 0. 01 mm/s • Transverse velocity limit. – Vvertical = 5 m/s => slope error < 2 10 -6. hard but possible 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 30

Straight Rails for Air Slide • Keeping the slope error < 2 10 -6 is well within the capability of today’s optical fabrication techniques. – Could do better, even if we needed general non-flat shape. $(0. 3 – 3) 105 • It is just within the capability of the precision granite industry. – $(4 - 7) 103 • Active system could compensate for irregular surface of rails, if needed. – E. g. , PZT at each bearing and (averaged) inertial sensors. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 31

Motion System, Cont. • Identified replacement motor controller that will permit still lower noise level. – Eliminates 5 μm encoder discretization. – More flexible and transparent control model. – Not known to be needed. 9/6/2021 Reasenberg & Phillips Quantum to Cosmos 32
- Slides: 32