A knitting algorithm for calculating Green functions in

A knitting algorithm for calculating Green functions in quantum systems Kyryl Kazymyrenko, Xavier Waintal CEA SPEC Saclay, France cond-mat/0711. 3413

Quantum transport calculations: Systems: Ø Heterostructures (2 D electron gas) Ø Graphene Ø Broken junctions Ø …. à Conductance, local density of states, shot noise…. Theoretical approaches: Ø Laundauer-Buttiker Ø Non-Equilibrium Green Function

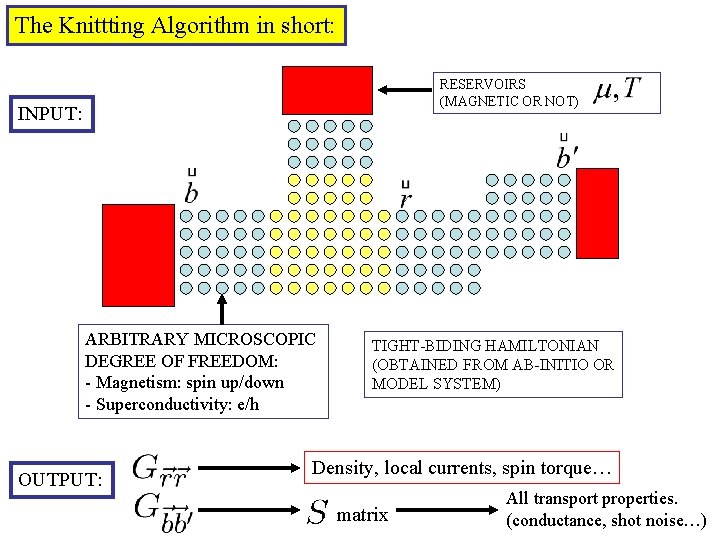
The Knittting Algorithm in short: RESERVOIRS (MAGNETIC OR NOT) INPUT: ARBITRARY MICROSCOPIC DEGREE OF FREEDOM: - Magnetism: spin up/down - Superconductivity: e/h OUTPUT: TIGHT-BIDING HAMILTONIAN (OBTAINED FROM AB-INITIO OR MODEL SYSTEM) Density, local currents, spin torque… matrix All transport properties. (conductance, shot noise…)

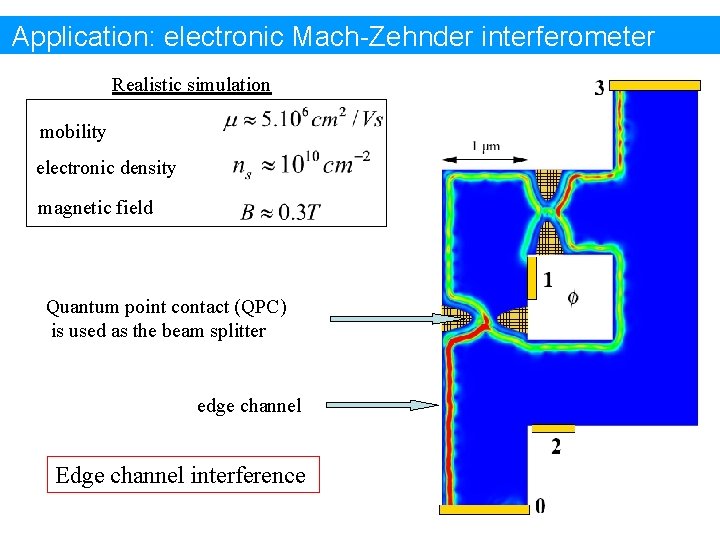
Application: electronic Mach-Zehnder interferometer Realistic simulation mobility electronic density magnetic field Quantum point contact (QPC) is used as the beam splitter edge channel Edge channel interference

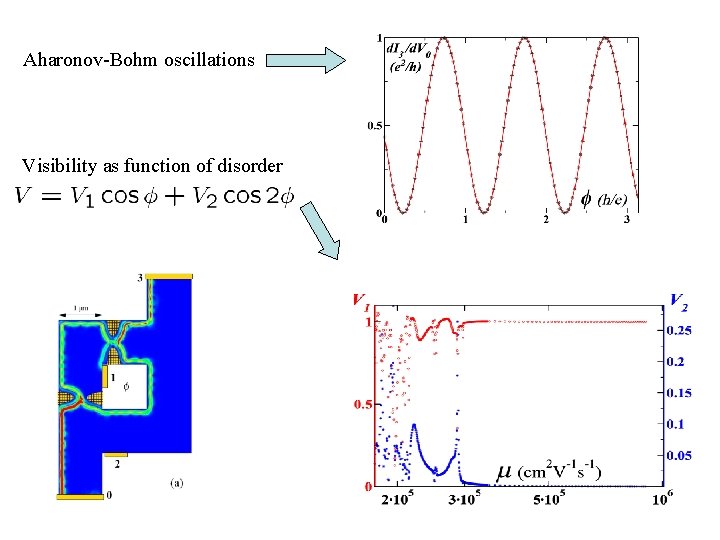
Aharonov-Bohm oscillations Visibility as function of disorder

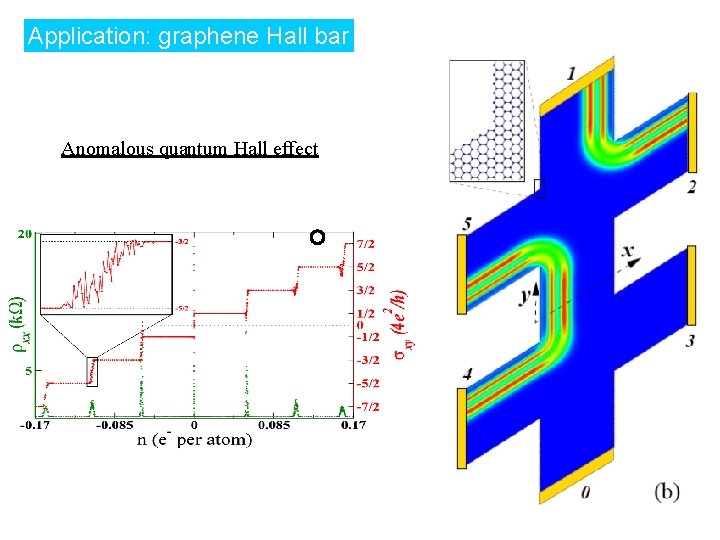
Application: graphene Hall bar Anomalous quantum Hall effect

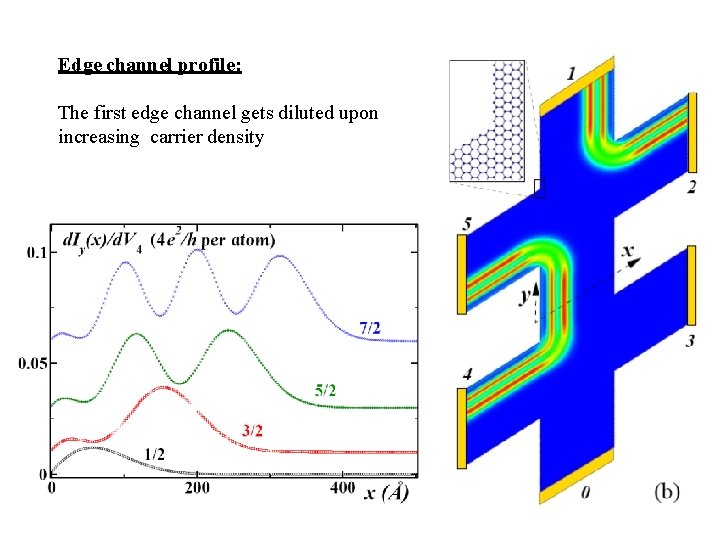
Edge channel profile: The first edge channel gets diluted upon increasing carrier density

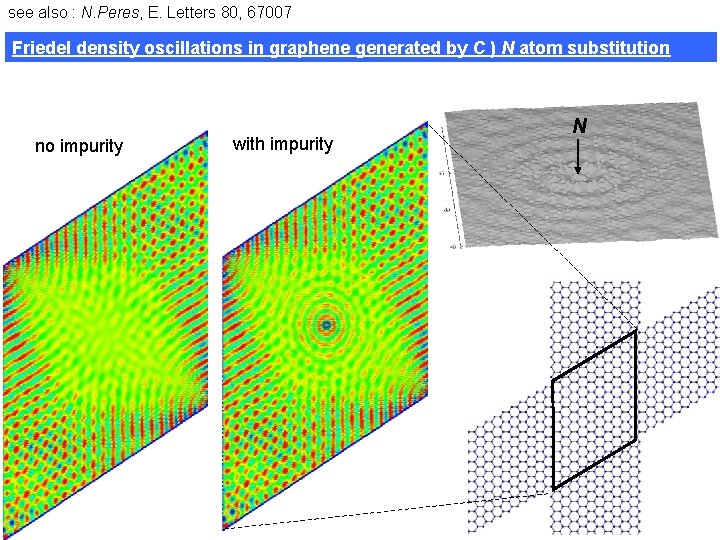
see also : N. Peres, E. Letters 80, 67007 Friedel density oscillations in graphene generated by C ) N atom substitution no impurity with impurity N

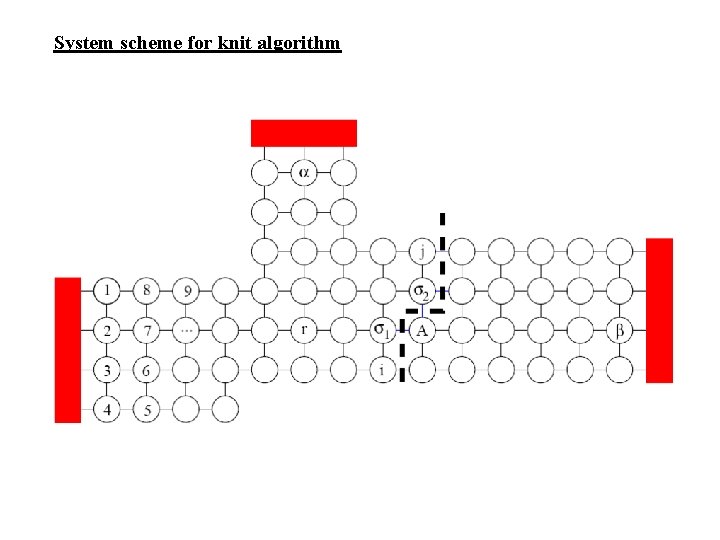
System scheme for knit algorithm

A user friendly Python interface… V=knit. scalar. M(1. ) Hd=knit. scalar. M(0. ) E=-4+1 phi=0. Lx=5 Ly=5 a=knit. rectangle([Lx, 3*Ly+2*Lx], [Lx, 0], V, Hd) a. coller(knit. rectangle([3*Lx, Lx], [0, Ly], V, Hd)) a. coller(knit. rectangle([3*Lx, Lx], [0, 2*Ly+Lx], V, Hd)) contacts=[] contacts. append([knit. unreservoir. N(knit. rectangle([Lx, 1], [Lx, 0], V, Hd), V, phi), "DOWN"]) contacts. append([knit. unreservoir. N(knit. rectangle([Lx, 1], [Lx, 3*Ly+2*Lx-1], V, Hd), V, phi), "UP"]) contacts. append([knit. unreservoir. N(knit. rectangle([1, Lx], [0, Ly], V, Hd), V, phi), "LEFT"]) contacts. append([knit. unreservoir. N(knit. rectangle([1, Lx], [3*Lx-1, Ly], V, Hd), V, phi), "RIGHT"]) contacts. append([knit. unreservoir. N(knit. rectangle([1, Lx], [0, 2*Ly+Lx], V, Hd), V, phi), "LEFT"]) contacts. append([knit. unreservoir. N(knit. rectangle([1, Lx], [3*Lx-1, 2*Ly+Lx], V, Hd), V, phi), "RIGHT"]) ring=knit. systemtotal(a, contacts[0][0]) for i in range(len(contacts)-1): ring. addlead(contacts[i+1][0]) gas 2 D. add_white_disorder(ring, 0. 3, 666) s=sys. argv[0] system. visu 2 D(ring, s+". systeme") os. system("gv "+s+". systeme. eps & ") N=41 for phi_i in range(N): phi=+0. 6*(float(phi_i)/N) gas 2 D. add_magnetic_flux(ring, contacts, phi) s=obs. conductance_matrix(ring, E) gg=linear_least_squares(s, array((1. , 0. , -1. , 0. )))[0] print phi, gg[3]-gg[2], gg[5]-gg[4], gg[1]-gg[2], gg[5]-gg[4]

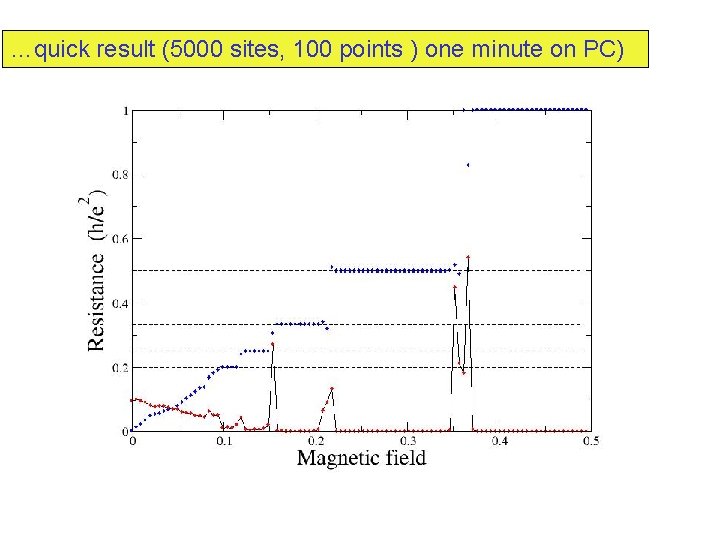
…quick result (5000 sites, 100 points ) one minute on PC)