A klasszikus termodinamika kritikja A klasszikus termodinamika tovbbfejlesztst

A klasszikus termodinamika kritikája • A klasszikus termodinamika továbbfejlesztését célzó elméletek többé-kevésbé az említett hiányosságokat igyekeztek vagy igyekeznek kiküszöbölni, egyszer a logikai-matematikai szerkezetre másszor pedig a fizikai tartalomra összpontosítva. RACIONÁLIS TERMODINAMIKA, SZTOCHASZTIKUS (STATISZTIKUS) TERMODINAMIKA IRREVERZÍBILIS FOLYAMATOK TERMODINAMIKÁJA

IRREVERZÍBILIS FOLYAMATOK TERMODINAMIKÁJA • Póta György: Modern fizikai kémia (Digitális Tankönyvtár, 2013), 1. 3 és 1. 4 fejezet

Irreverzíbilis folyamatok termodinamikája • Thermodynamics of Irreversible Processes, TIP Josef Meixner (1908 – 1994) német elméleti fizikus Sybren Ruurds de Groot (1916 – 1994) holland fizikus Ilya Prigogine [Илья Рома нович Приго жин] Lars Onsager 1903 – 1976) norvég fiziko-kémikus kémiai Nobel-díj (1968) (1917 – 2003) orosz származású belga–amerikai kémikus, kémiai Nobel-díj (1977)

Irreverzíbilis folyamatok termodinamikája • A terület kiemelkedő hazai kutatói: Gyarmati István (1929 – 2002) fizikus, kémikus Fényes Imre (1917 – 1977) fizikus

Irreverzíbilis folyamatok termodinamikája • Tartalmilag az irreverzíbilis folyamatok termodinamikája az összetett transzportjelenségek vizsgálatával szoros kapcsolatban alakult ki, • eredményeinek jelentős része az egyensúlyhoz közeli nyílt rendszerekre vonatkozik. • Alapfeltevés, hogy a klasszikus termodinamikában időtől függetlenül megfogalmazott összefüggések időbeli változásokra is érvényesek. • Az elmélet ún. nemfolytonos rendszerekre vonatkozó alakjával fogunk részletesebben foglalkozni (ez matematikailag egyszerűbb).

A nemfolytonos rendszer • Vegyünk egy melegebb és egy hidegebb fémtömböt, amelyeket egy hőszigetelő fólia választ el egymástól. • A melegebb tömbből hő jut át a hidegebbe, de a hőszigetelő fólia miatt viszonylag lassú a hőátadási folyamat, s ezalatt a tömbök belsejében az esetleg keletkezett hőmérsékleti inhomogenitásoknak van idejük kiegyenlítődni, a tömbök így a folyamat alatt termikusan homogénnek vehetők. • A hőcsere folyamata az egyes tömbök szempontjából reverzíbilisnek tekinthető, a teljes rendszer szempontjából azonban irreverzíbilis.
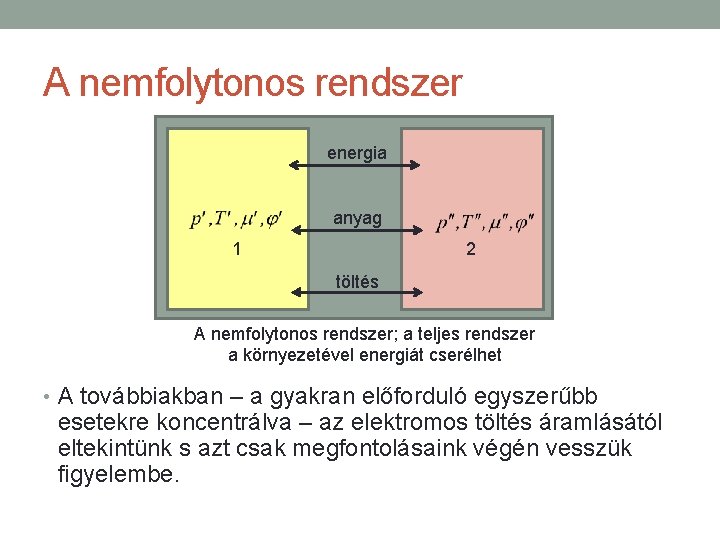
A nemfolytonos rendszer energia anyag 1 2 töltés A nemfolytonos rendszer; a teljes rendszer a környezetével energiát cserélhet • A továbbiakban – a gyakran előforduló egyszerűbb esetekre koncentrálva – az elektromos töltés áramlásától eltekintünk s azt csak megfontolásaink végén vesszük figyelembe.

Az entrópiaprodukció • A két alrendszerre: • Mivel a teljes (1+2) rendszer zárt: • Ha az egyes rendszerek hőeffektusait felosztjuk belsőre (a másik alrendszerrel cserélt hő) és külsőre (környezettel cserélt hő): • A teljes (1+2) rendszerre az első főtétel: Ebben csak a rendszer és a környezete közötti kölcsönhatások szerepelnek, a két alrendszer közötti kölcsönhatások nem.

Az entrópiaprodukció • A korábbiak kombinálásával: • Gibbs-egyenlet alkalmazása (mivel a két alrendszer minden pillanatban egyensúlyban van): 1. előadás anyagából:
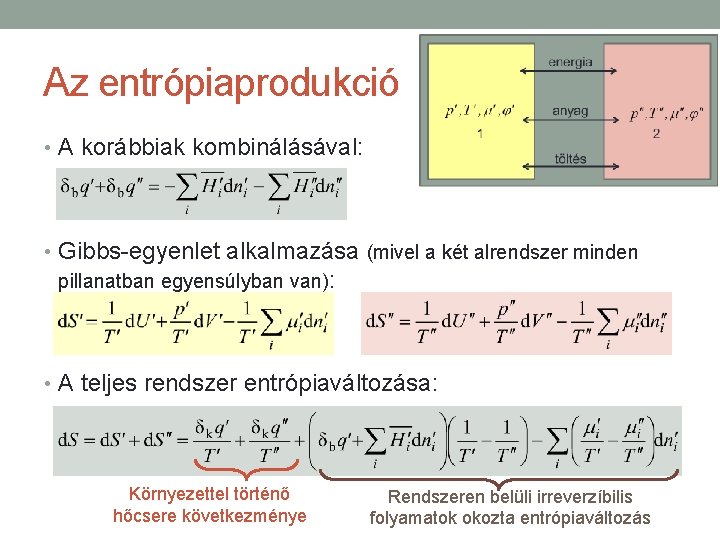
Az entrópiaprodukció • A korábbiak kombinálásával: • Gibbs-egyenlet alkalmazása (mivel a két alrendszer minden pillanatban egyensúlyban van): • A teljes rendszer entrópiaváltozása: Környezettel történő hőcsere következménye Rendszeren belüli irreverzíbilis folyamatok okozta entrópiaváltozás
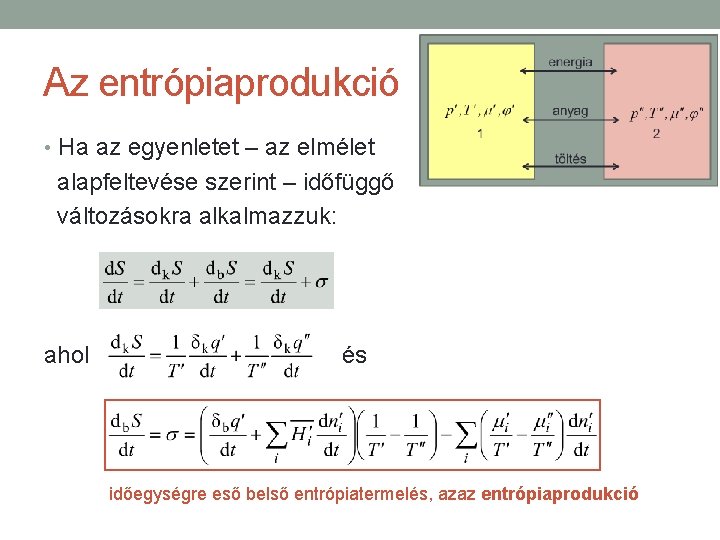
Az entrópiaprodukció • Ha az egyenletet – az elmélet alapfeltevése szerint – időfüggő változásokra alkalmazzuk: ahol és időegységre eső belső entrópiatermelés, azaz entrópiaprodukció

Az entrópiaprodukció A második főtétel miatt az entrópiaprodukció… • valóságos, irreverzíbilis folyamatokra mindig pozitív, • reverzíbilis folyamatokban pedig eltűnik, azaz σ = 0. A σ kifejezését általánosíthatjuk arra az esetre, amikor a rendszerben elektromos potenciál és töltés jelenlétével is számolnunk kell: ahol φ′ és φ″ az egyes alrendszerek elektromos potenciáljai, de′/dt pedig az 1 alrendszer egységnyi időre eső töltésváltozása (azaz elektromos áram).

Áramok és erők • Az irreverzíbilis folyamatok termodinamikájának Onsager- féle elméletében központi szerepük van az általánosított áramoknak és erőknek. • Az általánosított áram mindig valamilyen extenzív mennyiség árama, • a hozzá tartozó általánosított erő az adott áram létrehozásához hozzájáruló inhomogenitás mértéke.
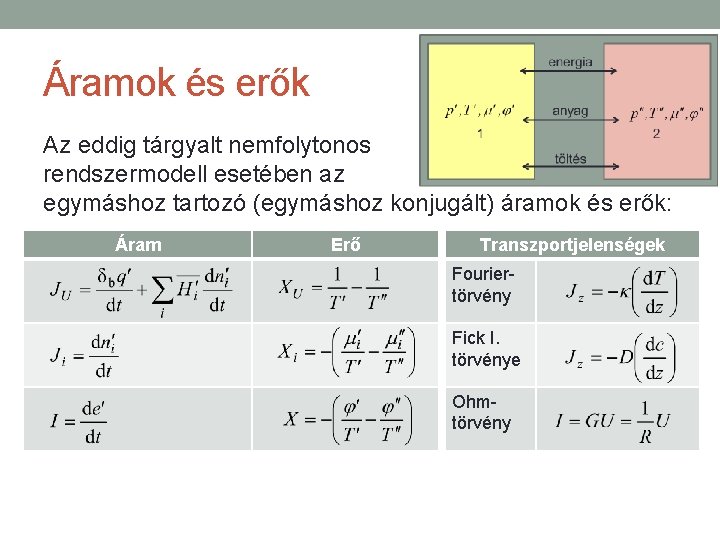
Áramok és erők Az eddig tárgyalt nemfolytonos rendszermodell esetében az egymáshoz tartozó (egymáshoz konjugált) áramok és erők: Áram Erő Transzportjelenségek Fouriertörvény Fick I. törvénye Ohmtörvény

Áramok és erők Áram Erő • Az így definiált erőkkel és áramokkal az entrópiaprodukció: , általánosan

Áramok és erők • Az általános képletben Jk és Xk már nem az anyagtranszport mennyiségeit jelentik, hanem teljes általánosságban egymáshoz tartozó áram-erő párost. • Az egyes konkrét alkalmazásoknál az áramok és erők mibenléte – fizikai alapokon – általában jól megállapítható. Nincs azonban az áramoknak és erőknek általános érvényű, formális, matematikai definíciójuk. (Ez az Onsager-elmélet egyik vitatható pontja. ) • Az így definiált erőkkel és áramokkal az entrópiaprodukció: , általánosan

Onsager-féle reciprocitási relációk • Az erők áramokat hozhatnak létre, s lehetséges, hogy egy- egy adott áram kialakulásához több erő is hozzájárulhat. Onsager feltevése szerint – legalábbis az egyensúly környezetében – az áramok és az erők között lineáris kapcsolat van. • Legegyszerűbb eset: 2 áram és 2 erő (2× 2 -es rendszer) Lxy: vezetési együtthatók Elvben mindkét erő befolyásolhatja mindkét áram nagyságát. • Onsager kísérleti eredmények és (más tudományágakból származó) elméleti megfontolások alapján feltételezte, hogy a szimmetrikus helyzetű vezetési együtthatókra teljesül az ún. reciprocitási reláció: L 12 = L 21

Onsager-féle reciprocitási relációk • Kereszteffektus: ha L 12 = L 21 ≠ 0 (azaz egy erő valóban befolyásol egy hozzá nem konjugált áramot) • Az entrópiaprodukció a 2× 2 -es rendszerben: • E kifejezés biztosan eltűnik, ha X 1 és X 2 egyaránt nulla. • Biztosítanunk kell azonban azt is, hogy a kifejezés nem csupa zérus erők esetén mindig pozitív legyen, hiszen ez σ jellemző fizikai tulajdonsága. Matematikai szempontból ún. pozitív definit kvadratikus formára van tehát szükségünk.

Onsager-féle reciprocitási relációk • Biztosítanunk kell azonban azt is, hogy a kifejezés nem csupa zérus erők esetén mindig pozitív legyen, hiszen ez σ jellemző fizikai tulajdonsága. Matematikai szempontból ún. pozitív definit kvadratikus formára van tehát szükségünk. • Ehhez teljesülni kell a következőknek: L 11 és L 22 > 0; L 11 L 22 – L 21 L 12 > 0

Onsager-féle reciprocitási relációk - általános rendszer • Az M számú áramot és M számú erőt tartalmazó rendszerben a fenomenológiai egyenletek a következők: • Az Onsager-féle reciprocitási relációk alakja: Lik = Lki amit másként úgy is mondhatunk, hogy a vezetési együtthatók {Lik} mátrixa szimmetrikus. • Kereszteffektus jön létre akkor, ha Lik = Lki ≠ 0 • Az entrópiaprodukció kifejezése: Ennek pozitívnak kell lennie, hacsak egyetlen Xi erő is eltér 0 -tól.

Onsager-féle reciprocitási relációk - általános rendszer • Az entrópiaprodukció kifejezése ezúttal tehát egy M- dimenziós, pozitív definit kvadratikus forma. Ahhoz, hogy ez teljesüljön, az Lik vezetési együtthatóknak további feltételeknek kell eleget tenniük. • Az Onsager-féle reciprocitási relációk • eredete, • bizonyíthatósága, • szükségessége vita tárgya.

Az Onsager-elmélet kritikája - matematikai • Az Onsager-elmélet alapjait érintő kritika, hogy az áramok és az erők formális (matematikai) definíciója híján a reciprocitási relációknak, azaz L szimmetrikus voltának nincs valódi fizikai tartalma.

Az Onsager-elmélet kritikája - fizikai • Az Onsager-relációk haszontalanok, mert csak kevés olyan jelenség van, ahol az L mátrixnak nem csupán bizonyos elemeire van szükség, hanem az egészre. • Nem világos, hogy L szimmetrikus volta posztulátumnak veendő-e vagy bizonyításra szoruló tételnek. Ha az utóbbi érvényes, kérdéses, hogy mi a bizonyítás, vajon a más (pl. statisztikus) fizikai elméletekből származó megfontolások bizonyításnak tekinthetők-e. • Az is felmerül, hogy az Onsager-relációk hibásak vagy az elgondoltnál korlátozottabb hatókörűek, amennyiben bizonyos jelenségek értelmezése e relációkkal nem lehetséges, hibás eredményeket kapunk.

Minimális entrópiaprodukció elve • Izolált rendszer egyensúlyi állapotában az erők és az áramok eltűnnek, az entrópia pedig maximális lesz. DE: van-e valamilyen hasonló elv a nyílt rendszerben fellépő stacionárius állapot esetében? • Prigogine: az egyensúlyhoz közeli – azaz lineáris – rendszerek stacionárius állapotaiban a rendszer entrópiaprodukciója minimális lesz. Ilya Prigogine [Илья Рома нович Приго жин] (1917 – 2003) orosz származású belga–amerikai kémikus, kémiai Nobel-díj (1977)

Minimális entrópiaprodukció elve • Legyen a rendszerhez tartozó X 1, X 2, …, XM erők közül az első j rögzített értékű. Ezt külső kényszerek – például anyagáramlás – segítségével érhetjük el. A rögzített erőkhöz tartozó áramok a stacionárius állapotban nem tűnnek el. • Az Xj+1, Xj+2, …, XM erők értéke viszont nem rögzített, a hozzájuk tartozó áramok – az erők nagyságának függvényében – változhatnak. • Ha izolált egyensúlyban minden áram eltűnik, logikus feltételezni, hogy nyílt rendszer egyensúlyhoz közeli stacionárius állapotában legalább a nem rögzített erőkhöz tartozó áramok eltűnnek:

Minimális entrópiaprodukció elve • Ebből következik, hogy az entrópiaprodukció – a nem rögzített erők függvényében – extremális lesz: és (reciprocitási reláció) • Ez biztosan teljesül, hiszen a jobb oldalon az eltűnő Jj+1, Jj+2, … JM áramok állnak.

Minimális entrópiaprodukció elve • A disszipált teljesítmény abszolút értéke ( ) állandó hőmérsékleten az entrópiaprodukcióval együtt minimumot ad. • A minimális entrópiaprodukció elve időbeli változásokra is megfogalmazható, a stacionárius állapothoz közelítő rendszerben ugyanis a nem rögzített erők értékei úgy változnak meg, hogy teljesüljön a következő összefüggés: (az egyenlőség a stacionárius állapotban érvényes. ) • Ez is arra utal, hogy az entrópiaprodukció időben csökkenve a stacionárius állapotban minimumot vesz fel. • A minimális entrópiaprodukció elve implicite a stacionárius állapot stabilitását is sugallja: a stacionárius állapotból kibillentett rendszer a külső zavarás megszűnte után visszatér ebbe az állapotba.

Általános evolúciós kritérium • P. Glansdorff és I. Prigogine alkotta meg. • Ez a kritérium a szerzők szerint az egyensúlytól távol is érvényes. • A minimális entrópiaprodukció elvét felhasználva levezethető az egyensúlyhoz közeli rendszerekre. • Mivel a σ entrópiaprodukció az erők és áramok függvénye, változására felírható a következő: ahol és • Fenomenológikus egyenlet:

Általános evolúciós kritérium • Az entrópiaprodukció áramokat tartalmazó tagja: • Az entrópiaprodukció erőket tartalmazó tagja: (mivel az indexek és az összegzés sorrendje is felcserélhető) • Az Onsager-féle reciprocitási relációk értelmében Lik = Lki, emiatt pedig d. Jσ = d. Xσ és dσ = d. Jσ + d. Xσ = 2 d. Xσ • Ezt az egyenletet időbeli változásokra felírva és átrendezve:

Általános evolúciós kritérium • Az általános evolúciós kritériumot a alkalmazásával kapjuk (az egyenlőség a stacionárius állapotra vonatkozik):

Általános evolúciós kritérium • Az általános evolúciós kritériumot a alkalmazásával kapjuk (az egyenlőség a stacionárius állapotra vonatkozik): • Az általános evolúciós kritériumból megítélhető, hogy egy adott rendszert a stacionárius állapotából kimozdítva az várható-e, hogy a rendszer visszatér ebbe az állapotba vagy pedig „evolúció” indul meg, a rendszer a stacionárius pontjától eltávolodva új viselkedésformákat vesz fel, ún. disszipatív szerkezetek jönnek létre.

Általános evolúciós kritérium • Legyenek c 1, c 2, …, c. N a vizsgált rendszert jellemző változók (reaktor esetében pl. a reagáló anyagok koncentrációi). Ezekkel σ és d. Xσ kifejezhető. • Előfordul, hogy d. Xσ a rendszer valamilyen tulajdonságát leíró g(c 1, c 2, …, c. N) függvény teljes differenciálja, azaz fennáll a következő összefüggés: (A g függvényt kinetikai potenciálnak is nevezik. ) Ekkor azonban a G(t) = g(c 1(t), c 2(t), …, c. N(t)) függvényre:

Általános evolúciós kritérium • Legyenek c 1, c 2, …, c. N a vizsgált rendszert jellemző változók (reaktor esetében pl. a reagáló anyagok koncentrációi). Ezekkel σ és d. Xσ kifejezhető. • Előfordul, hogy d. Xσ a rendszer valamilyen tulajdonságát leíró g(c 1, c 2, …, c. N) függvény teljes differenciálja, azaz fennáll a következő összefüggés: (A g függvényt kinetikai potenciálnak is nevezik. ) Ekkor azonban a G(t) = g(c 1(t), c 2(t), …, c. N(t)) függvényre:

Általános evolúciós kritérium • Ez akkor igaz, ha a stacionárius állapoton kívül vagyunk. • Eszerint tehát a G függvény szigorúan monoton csökken. • Ez kizárja, hogy a rendszerben olyan „evolúció” jöjjön létre, ami időben periodikus viselkedéshez vezet. Ha ugyanis a rendszert jellemző c 1, c 2, …, c. N függvények az idő periodikus függvényei, úgy G-re is igaz ugyanez.
- Slides: 34