A Kernelbased Support Vector Machine by Peter Axelberg

A Kernel-based Support Vector Machine by Peter Axelberg and Johan Löfhede

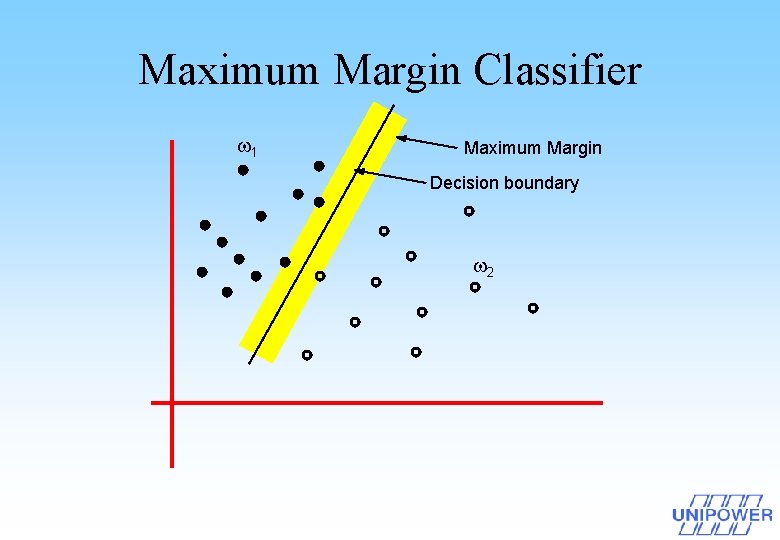
Maximum Margin Classifier 1 Maximum Margin Decision boundary 2

Need for more complex decision boundaries In general, real-world applications require more complex decision boundaries than linear functions.

Dimension expansion The SVM offers a method where the input space is mapped by a non-linear function, (x), to a higher dimensional feature space where the classes are more likely to be linearly separable.

High dimensional feature space xi (Xi) f( (Xi)) (x 1) 1 x 1 2 Input space High dimensional feature space Decision space

Kernel function Instead of directly using the mapping vectors (x) in the high dimentional feature space, a kernel function K(x, xi) can be introduced in the input space according to the following substitution: where < > denotes the inner product

The Kernel function used by the decision boundary function

Examples of Kernel functions q Polynomial q Radial basis function (RBF) q Sigmoidal

A real world example q Classification of some fruits/vegetables using kernel-based SVM

Feature 1 Feature 2 Feature 3 Feature 4

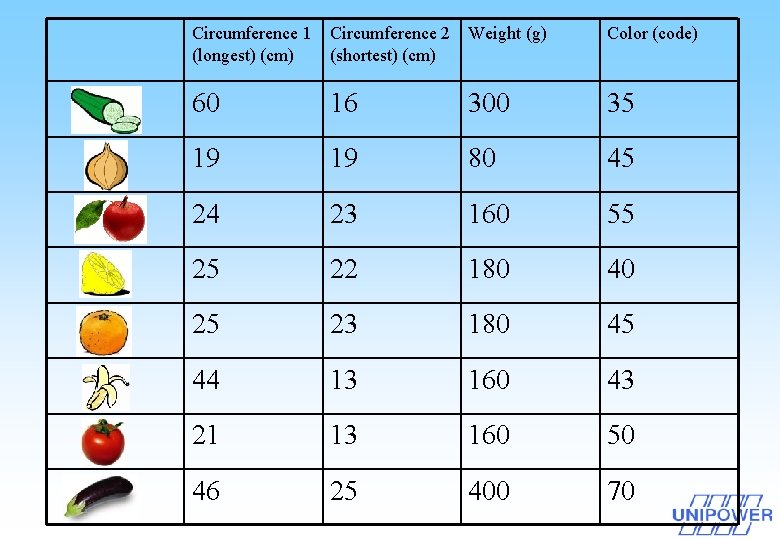
Circumference 1 (longest) (cm) Circumference 2 (shortest) (cm) Weight (g) Color (code) 60 16 300 35 19 19 80 45 24 23 160 55 25 22 180 40 25 23 180 45 44 13 160 43 21 13 160 50 46 25 400 70