A hybrid artificial bee colony algorithm for the

A hybrid artificial bee colony algorithm for the cooperative maximum covering location problem B. JAYALAKSHMI AND ALOK SINGH 2015

The Problem -The Cooperative Cover Location Problems: the Planar Case comes about in the paper by Berman, Drezner, and Krass (2009). -This is a Special Case of the Maximum Covering problem -In this case, facilities emit a “signal” that dissipates as distance increases and if the “signal” strength exceeds a certain threshold when it reaches a demand then the demand is covered. -The cooperative problem assumes that facilities cooperate to provide coverage to nodes.

Formulation of the Cooperative Maximum Covering Location (CMCLP) Problem

Example Cooperative Maximum Covering Problem P 3 1. 6 P 1 1. 8 P 2

Artificial Bee Covering (ABC) Algorithm First proposed by Karaboga in 2005 -This algorithm creates three groups of “bees”: scouts, employed, and onlooker -Initialize the algorithm by sending scouts to find initial food sources -Repeat: Send Employed Bees onto food sources and determine nectar amounts Calculate the probability value of the sources with which they are preferred by the onlooker bees Send onlooker bees onto food sources and determine their nectar amounts Stop the exploitation process of the sources exhausted by the bees Randomly, send the scouts to find new food sources Memorize the best food source found so far Stop

Bee Employment In the employed bee phase, the employed bees generate food sources in the proximity of its associated food source and evaluate food quality If the new food source is better than the employed bee moves to that food sources The bee employment phase ends when all employed bees finish this process than the onlooker phase begins

Bee Onlookers Employed bees share their information with onlookers Onlookers select food based on quality based on the fitness of the solution After onlookers select food sources they then determine food sources in the proximity and amongst all food sources in all neighborhoods the best quality food source is determined.

How and Why this Approach In employed bee phase all solutions are equally likely to improve While in the observer phase good quality solutions are more likely to improve than poor quality solutions The inclination toward selecting good quality solutions while searching in the proximity of good solutions for better solutions lends strength to the algorithm’s search for an optimal solution The scout bees randomly searching for new food sources aims to avoid the trap of local optima where our employed and observer bees might get honey trapped.

ABC Algorithm and the CMCLP

Determining an Initial Solution

Neighborhood Solution Generation

Other Features of the Algorithm If an employed bees solution does not improve for a specified number of iterations then the associated employed bee becomes a scout There are no restrictions on the number of scout bees in an iteration The scout bee is reemployed by assigning it to a new solution generated in the same way as our initial solution

Local Search as a Means of Improvement

Pseudocode

Computational Results Setup
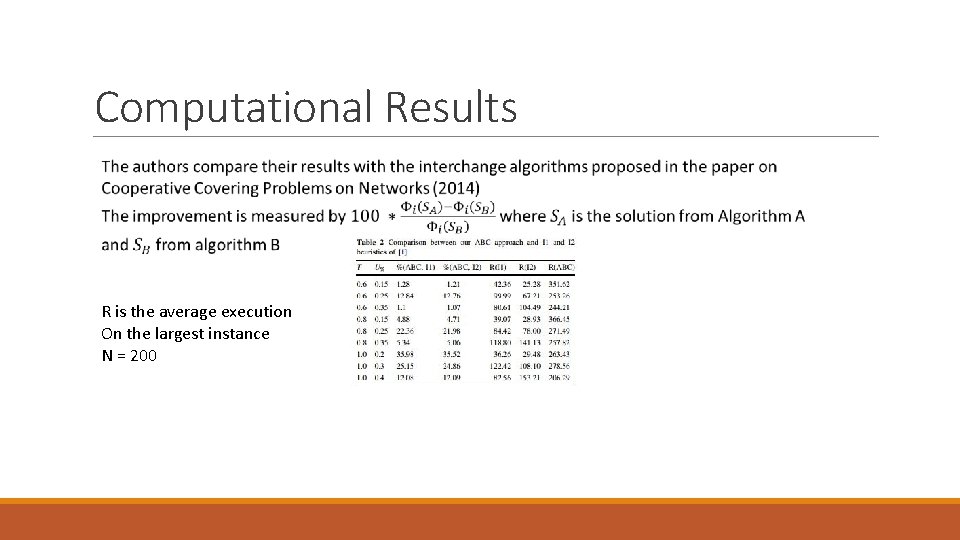
Computational Results R is the average execution On the largest instance N = 200

Conclusion The ABC algorithm outperforms the existing interchange algorithms in solution quality but are slower than the existing methods. This is the first metaheuristic presented for the CMCLP problem as tabu search and neighborhood that were experimented with only resulted in slight improvement over interchange and did not represent full metaheuristics. This papers shows how population based metaheuristics offer an appropriate tool in solving the CMCLP problem.

Questions ?
- Slides: 18