A Heap Implementation Chapter 26 1 Adapted from

A Heap Implementation Chapter 26 1 Adapted from Pearson Education, Inc.

Contents � Reprise: The ADT Heap � Using an Array to Represent a Heap � Adding an Entry � Removing the Root � Creating a Heap � Heap Sort 2 Adapted from Pearson Education, Inc.

Objectives � Use an array to represent a heap � Add an entry to an array-based heap � Remove the root of an array-based heap � Create a heap from given entries � Sort an array by using a heap sort 3 Adapted from Pearson Education, Inc.

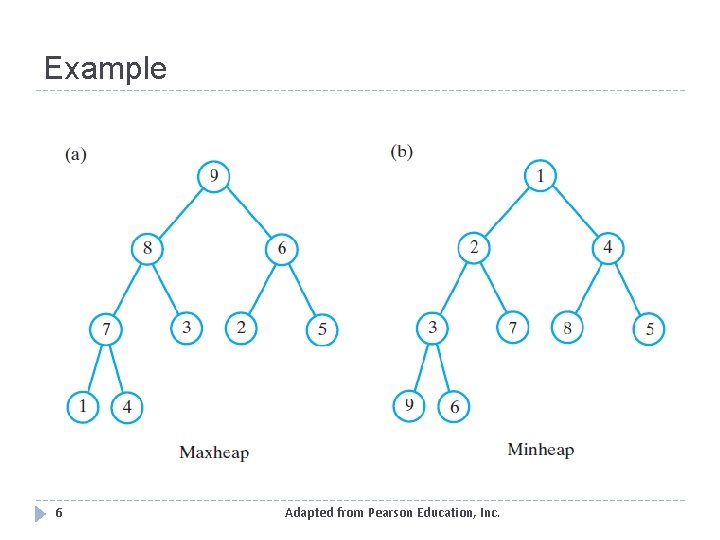
Heaps (ch 23) � Complete binary tree: nodes contain Comparable objects � Organization � Each node contains object no smaller (or no larger) than objects in descendants � Maxheap, object in node greater than or equal to descendant objects � Minheap, object in node less than or equal to descendant objects 4 Adapted from Pearson Education, Inc.

Reprise: The ADT Heap � Interface considered in Chapter 23 � Listing 23 -6 5 Adapted from Pearson Education, Inc.

Example 6 Adapted from Pearson Education, Inc.

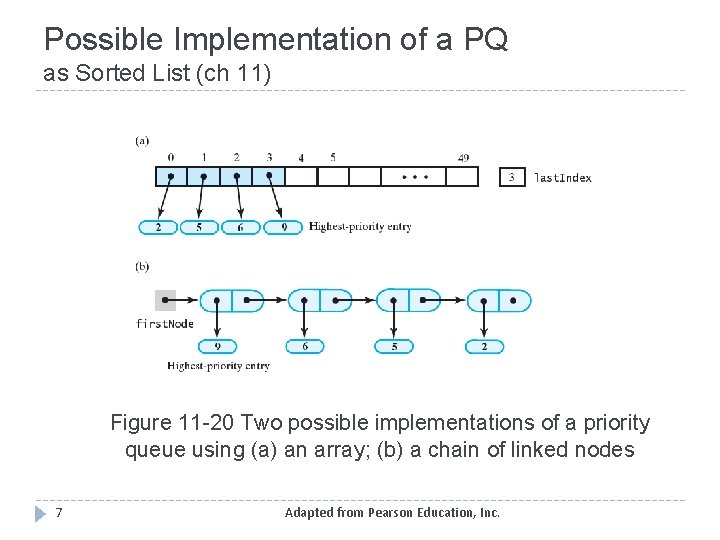
Possible Implementation of a PQ as Sorted List (ch 11) Figure 11 -20 Two possible implementations of a priority queue using (a) an array; (b) a chain of linked nodes 7 Adapted from Pearson Education, Inc.

Possible Implementation of a PQ as a Heap (ch 23) public class Priority. Queue <T extends Comparable<? super T >> implements Priority. Queue. Interface < T > { private Max. Heap. Interface < T > pq; public Priority. Queue () { pq = new Max. Heap < T > (); } // end default constructor public void add (T new. Entry) { pq. add (new. Entry); } // end add //Implementations of remove, peek, is. Empty, get. Size, and clear are here. } // end Priority. Queue 8 Adapted from Pearson Education, Inc.

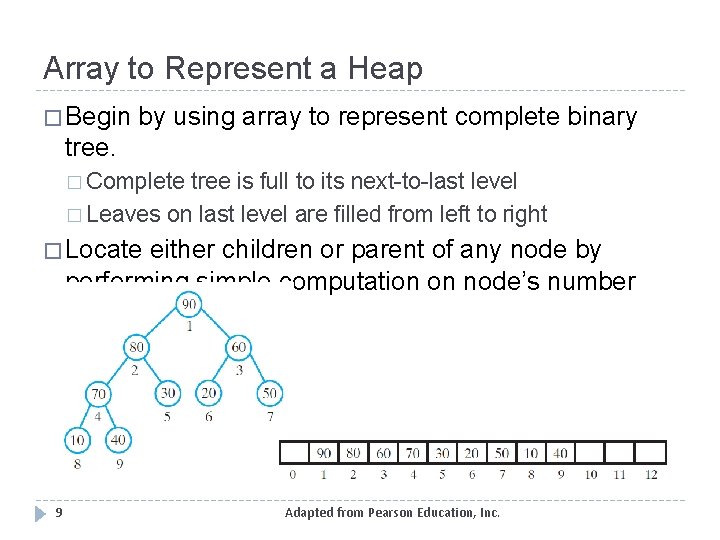
Array to Represent a Heap � Begin by using array to represent complete binary tree. � Complete tree is full to its next-to-last level � Leaves on last level are filled from left to right � Locate either children or parent of any node by performing simple computation on node’s number 9 Adapted from Pearson Education, Inc.

Array to Represent a Heap � View code of class Max. Heap, Listing 26 -1 � Data fields: � Array of Comparable heap entries � Index of last entry in the array � A constant for default initial capacity of heap 10 Adapted from Pearson Education, Inc.

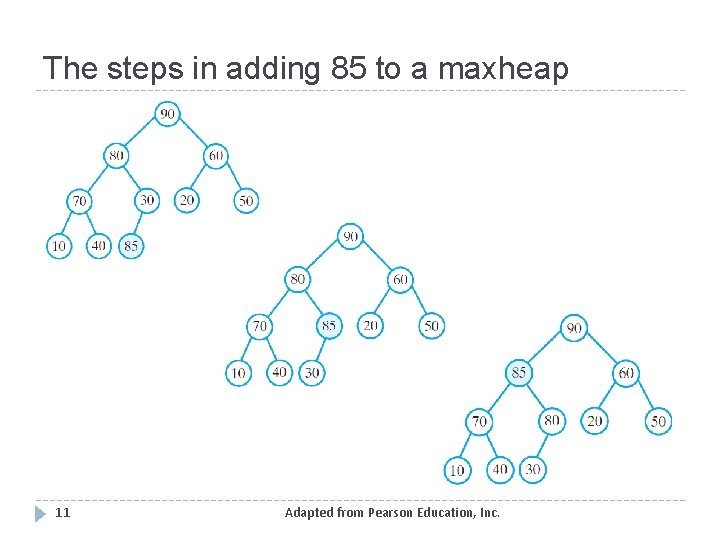
The steps in adding 85 to a maxheap 11 Adapted from Pearson Education, Inc.

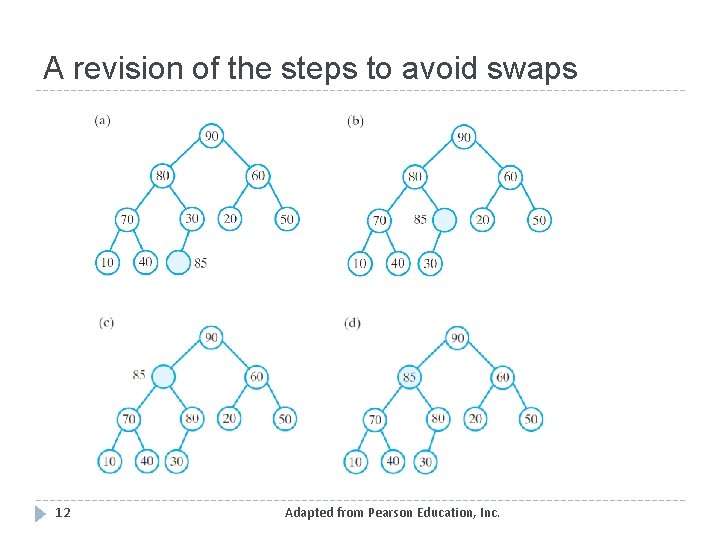
A revision of the steps to avoid swaps 12 Adapted from Pearson Education, Inc.

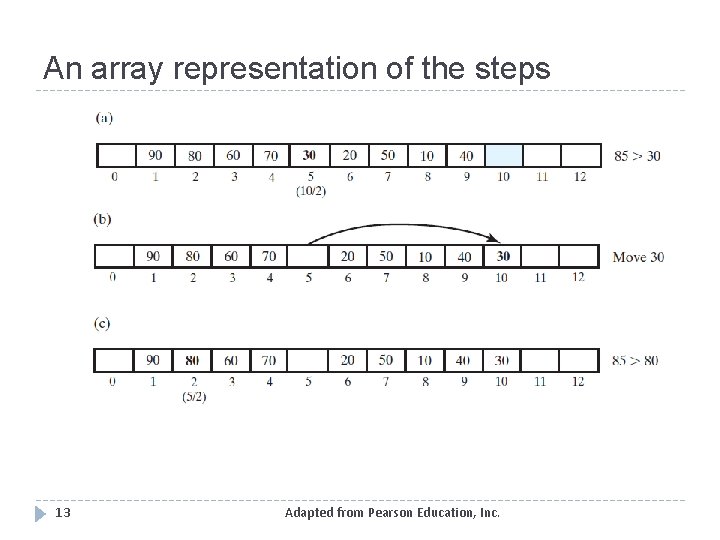
An array representation of the steps 13 Adapted from Pearson Education, Inc.

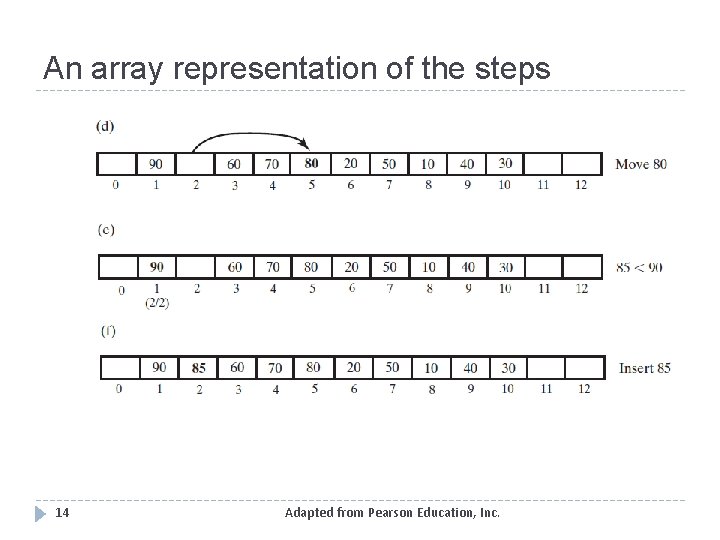
An array representation of the steps 14 Adapted from Pearson Education, Inc.

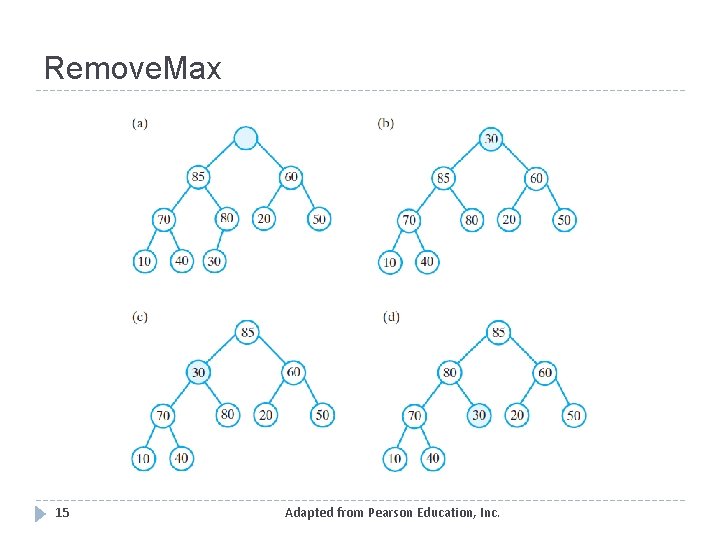
Remove. Max 15 Adapted from Pearson Education, Inc.

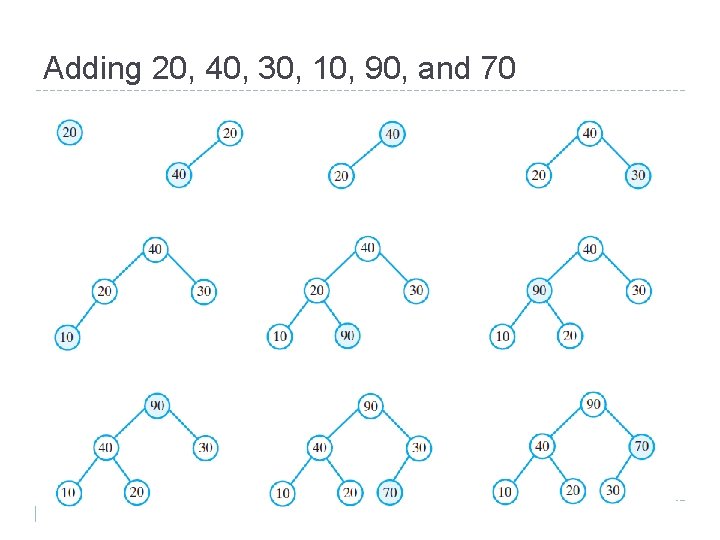
Adding 20, 40, 30, 10, 90, and 70 16 Adapted from Pearson Education, Inc.

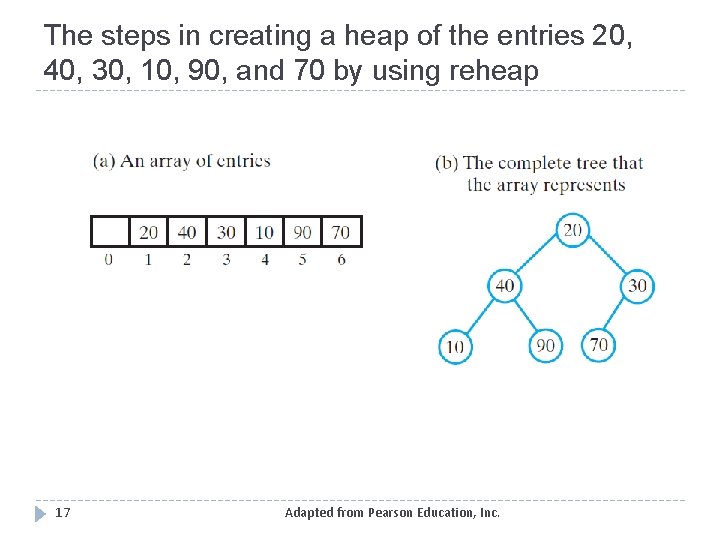
The steps in creating a heap of the entries 20, 40, 30, 10, 90, and 70 by using reheap 17 Adapted from Pearson Education, Inc.

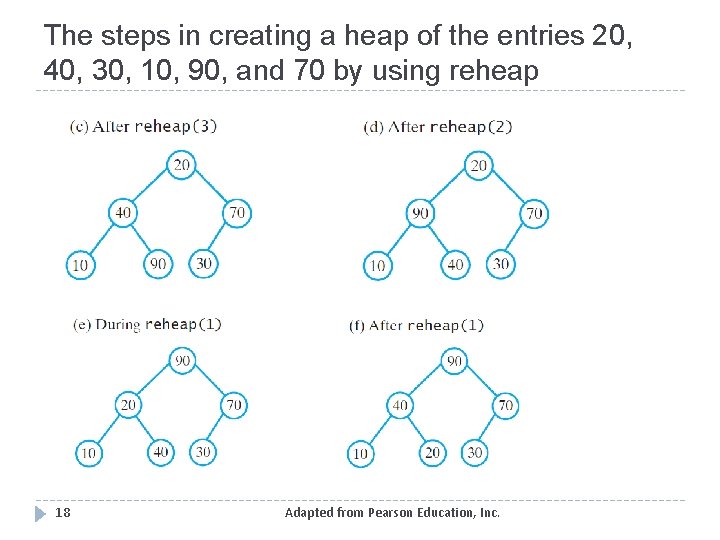
The steps in creating a heap of the entries 20, 40, 30, 10, 90, and 70 by using reheap 18 Adapted from Pearson Education, Inc.

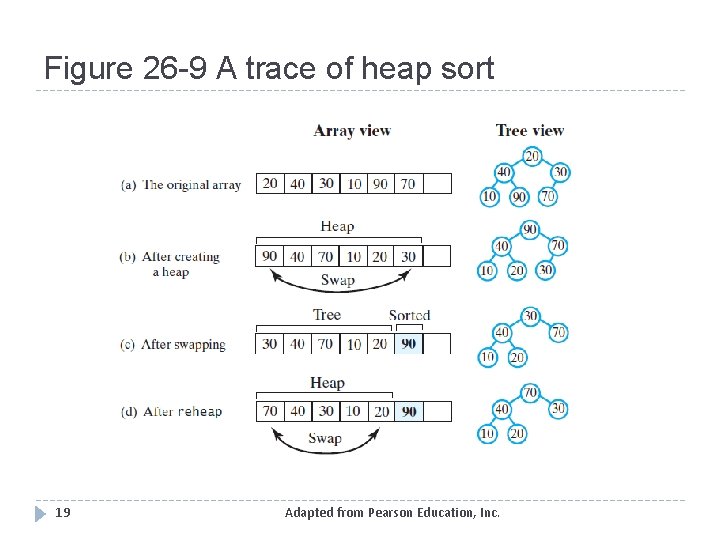
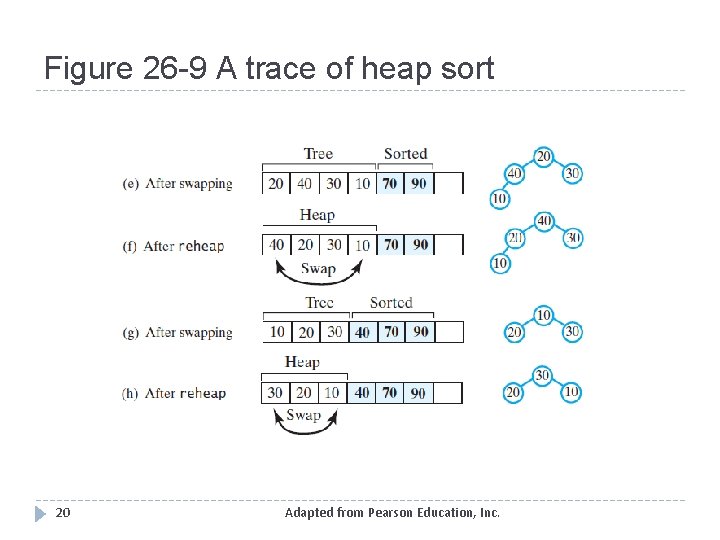
Figure 26 -9 A trace of heap sort 19 Adapted from Pearson Education, Inc.

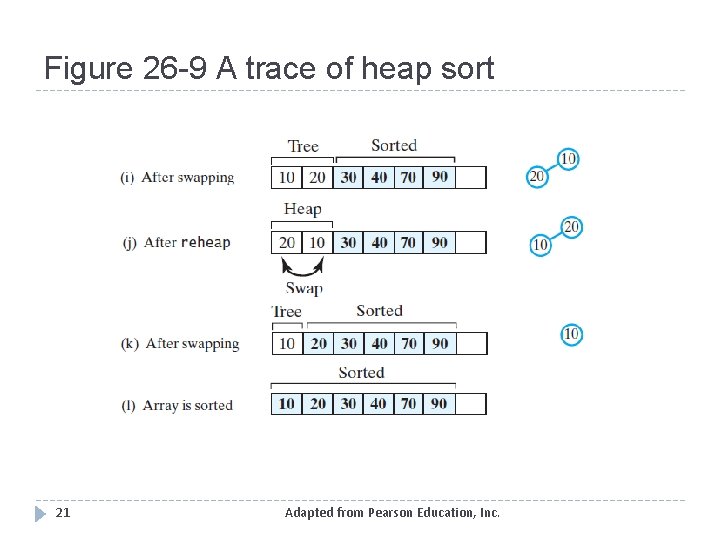
Figure 26 -9 A trace of heap sort 20 Adapted from Pearson Education, Inc.

Figure 26 -9 A trace of heap sort 21 Adapted from Pearson Education, Inc.

Efficiency � 22 Adapted from Pearson Education, Inc.

End Chapter 26 23 Adapted from Pearson Education, Inc.