A guide to statistics in A Level Geography

A guide to statistics in A Level Geography

Types of data • Nominal data – numbers – but used in categories (e. g. number of different types of shops in a CBD) • Ordinal data – numbers that can be put into order (e. g. results of bipolar survey) • Interval data – Similar to Ordinal – but the gap between numbers is constant (e. g. temperature) • Ratio data – similar to Interval but the results can be analysed using ratio i. e. traffic survey (there are twice as many cars in survey 1 than 2)

Hypothesis When using statistical tests you must first draw up two hypotheses 1) The null hypothesis – this is always there is no statistical difference / correlation – this must always be accepted unless the hypothesis can be accepted. 2) The Hypothesis – this is that there is a statistically significant difference / correlation

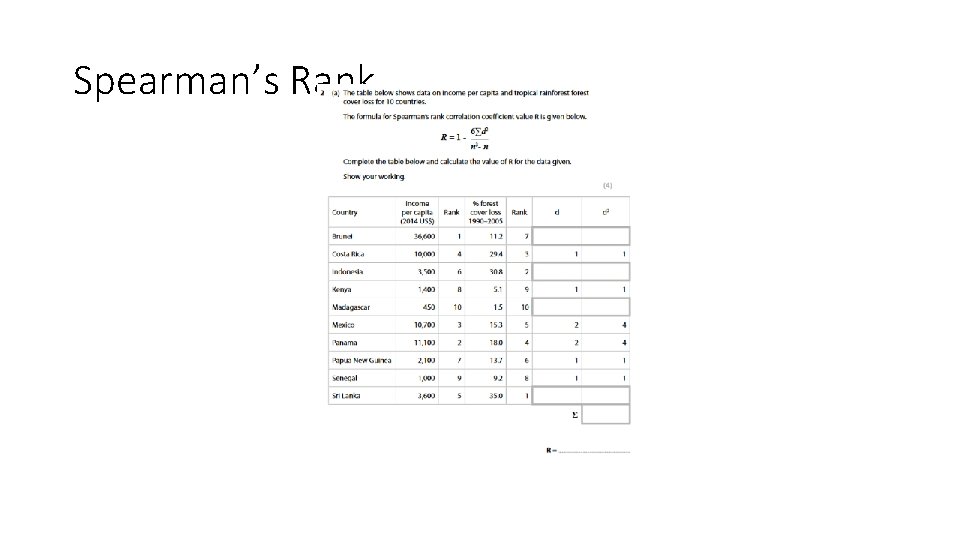
Spearman’s Rank

Spearman’s Rank • Used to test if two sets of variables are correlated • You must have 2 sets of variables for the same location / person • The data must be monotonic (you should be able to draw a straight line of best fit) • You normally must have 10 pairs of data to be statistically valid

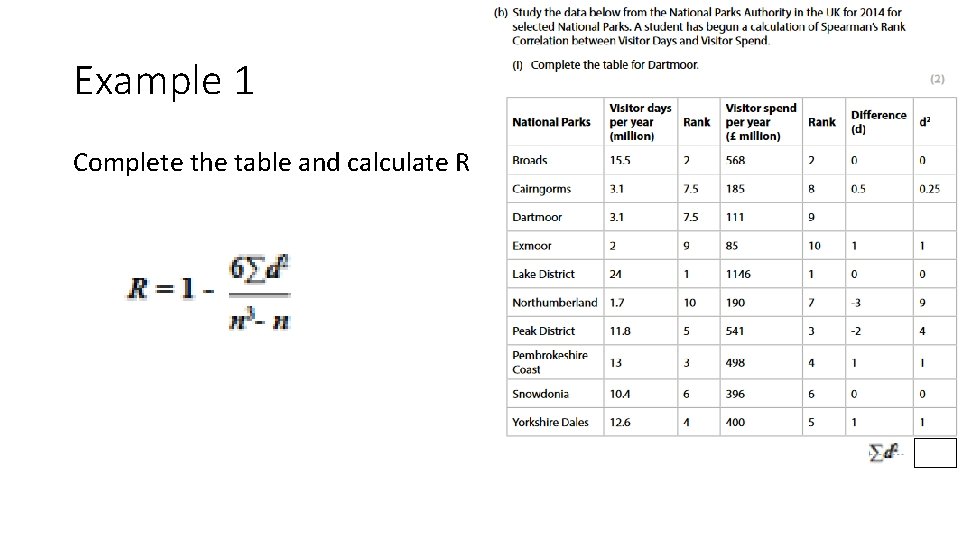
Example 1 Complete the table and calculate R

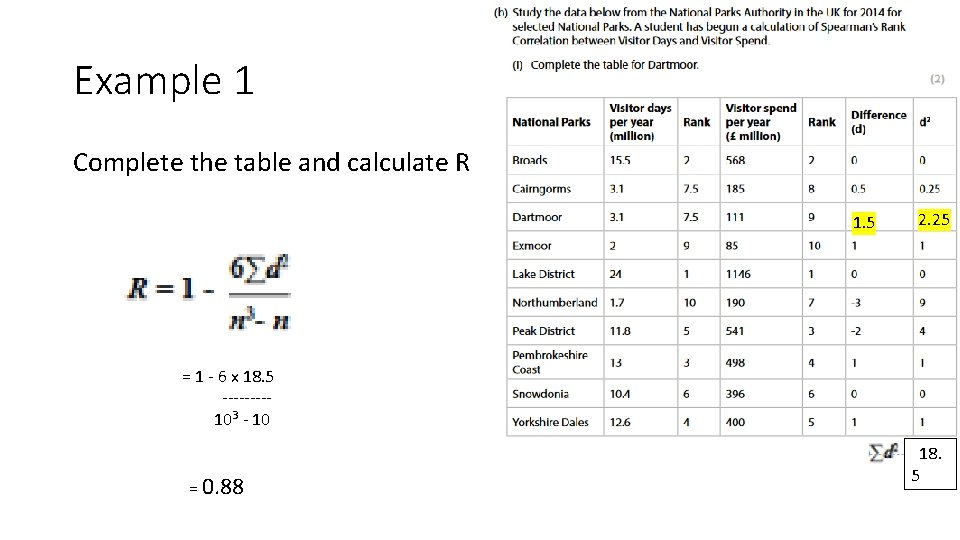
Example 1 Complete the table and calculate R 1. 5 2. 25 = 1 - 6 x 18. 5 ----103 - 10 = 0. 88 18. 5

Spearmans Rank Significance Once we have worked out R we need to check if it is significant It is significant if R is above the critical value – for n = 10 These are: As R = 0. 88 it is greater than 0. 78 i. e. there is a 99% chance that our data is correlated and not due to chance. We should therefore accept the hypothesis and reject the Null hypothesis

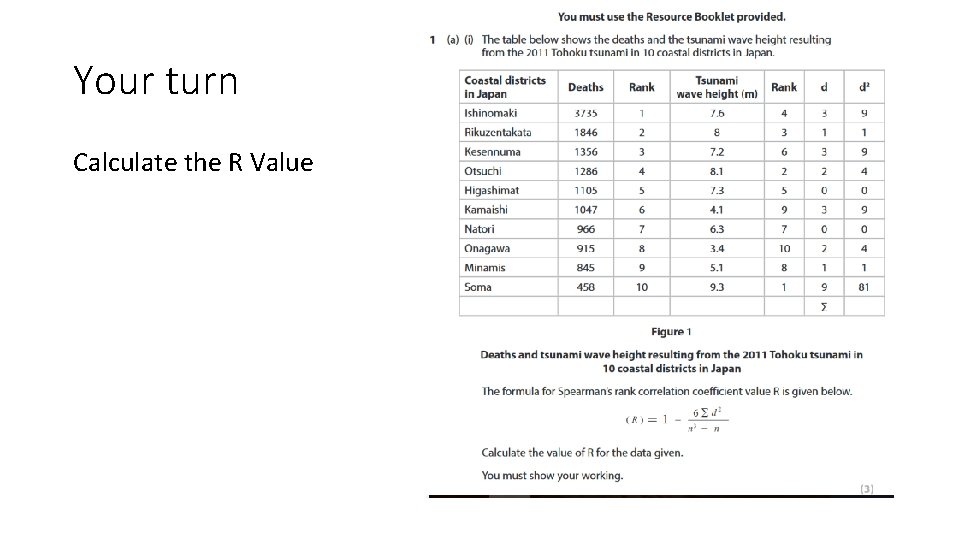
Your turn Calculate the R Value

What hypothesis should be accepted?

T test • • Used to see if there is a difference between two sets of data Compares the means of two sets of data You need at least two unrelated groups (e. g. male and female) Assumes data is normally distributed Uses interval or ratio data (numerical values) There is no minimum sample size – but 20 -30 is considered the norm Degrees of freedom is calculated as total sample size -2 Hypothesis will always be there is a statistical difference Null Hypotheis is always there is no statistical diffrence

T Test Exam question

T-Test formula = The mean (average) of sample 1 and 2 respectively S 1 / S 2 = Standard deviation of sample 1 and 2 respectively n 1 / n 2 = size of sample in data set 1 and 2 respectively

Chi 2 Test This is a comparative test. To use it you must have • the data are in the form of frequencies in a number of categories (i. e. nominal data). • there are more than 20 observations in total • The expected frequency for each category must be more than 4 • the observations are independent: one observation does not affect another. The same person cant be in both categories i. e. male / female - not brown eyes vs brown hair.

Chi 2 Test This is a comparative test. To use it you must have • the data are in the form of frequencies in a number of categories (i. e. nominal data). • there are more than 20 observations in total • The expected frequency for each category must be more than 4 • the observations are independent: one observation does not affect another. The same person cant be in both categories i. e. male / female - not brown eyes vs brown hair. • Degrees of freedom = number of categories -1

Chi Squared formula X 2= Chi squared value O = observed results E= Expected results ∑ = Sum of

Chi 2 Test The hypothesis is that there is a statistical difference The null hypothesis is that there isn’t a statistical difference Next draw up a table like this: For this sample df = n-1 = 2 The critical value for 0. 05 is 5. 99 We therefore reject the hypothesis and accept the Null hypothesis 2 3. 9