A Geometric Perspective on Machine Learning 1 Machine

A Geometric Perspective on Machine Learning 何晓飞 浙江大学计算机学院 1

Machine Learning: the problem Information (training data) f f: X→Y 何晓飞 X and Y are usually considered as a Euclidean spaces. 2

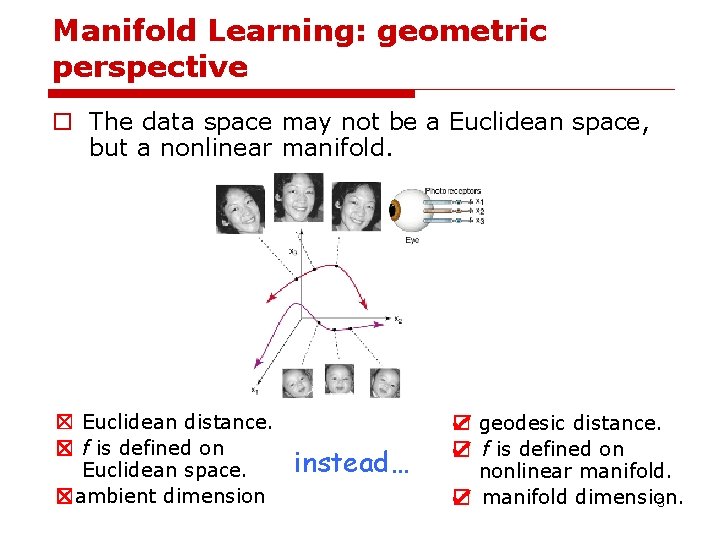
Manifold Learning: geometric perspective o The data space may not be a Euclidean space, but a nonlinear manifold. ☒ Euclidean distance. ☒ f is defined on Euclidean space. ☒ambient dimension instead… ☑ geodesic distance. ☑ f is defined on nonlinear manifold. ☑ manifold dimension. 3

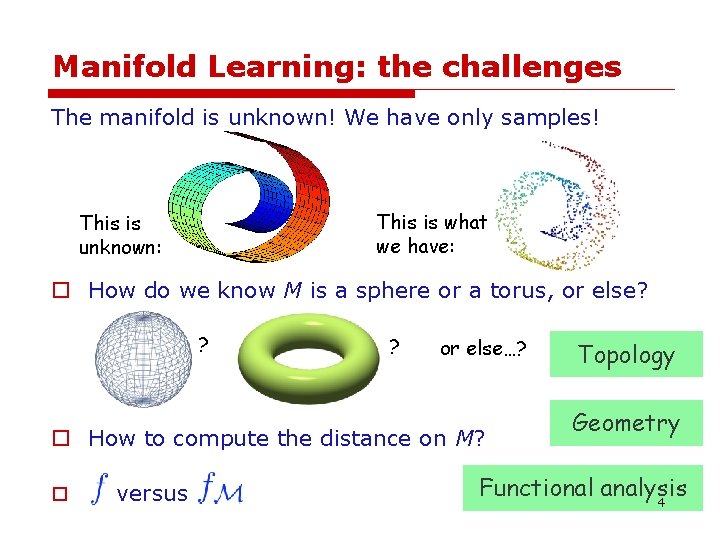
Manifold Learning: the challenges The manifold is unknown! We have only samples! This is what we have: This is unknown: o How do we know M is a sphere or a torus, or else? ? ? or else…? o How to compute the distance on M? o versus Topology Geometry Functional analysis 4

Manifold Learning: current solution o Find a Euclidean embedding, and then perform traditional learning algorithms in the Euclidean space. 5

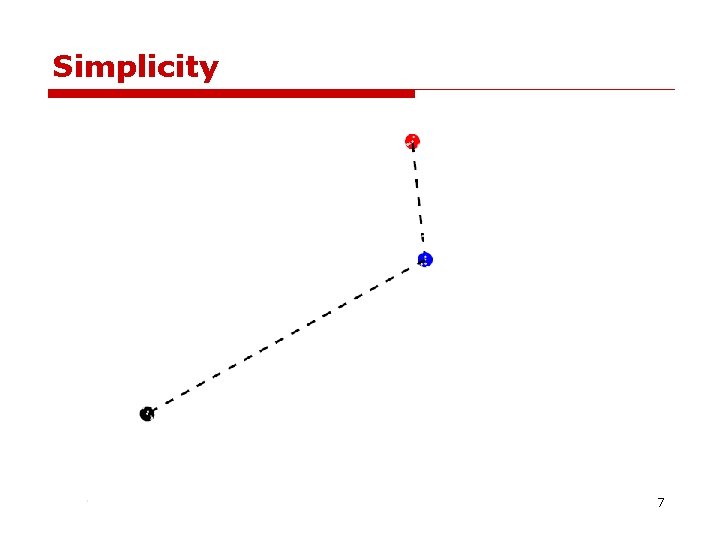
Simplicity 6

Simplicity 7

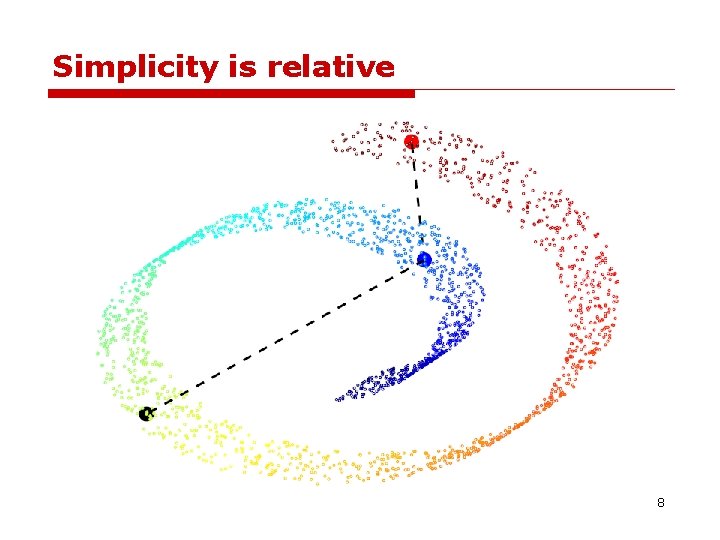
Simplicity is relative 8

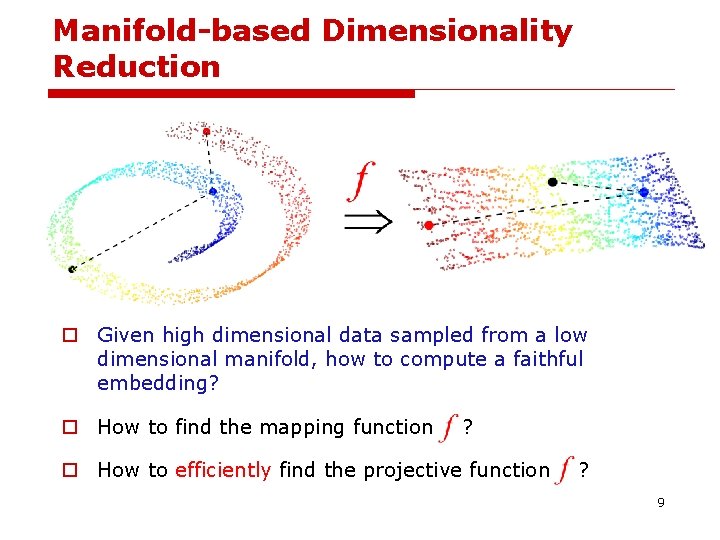
Manifold-based Dimensionality Reduction o Given high dimensional data sampled from a low dimensional manifold, how to compute a faithful embedding? o How to find the mapping function ? o How to efficiently find the projective function ? 9

A Good Mapping Function o If xi and xj are close to each other, we hope f(xi) and f(xj) preserve the local structure (distance, similarity …) o k-nearest neighbor graph: o Objective function: n Different algorithms have different concerns 10

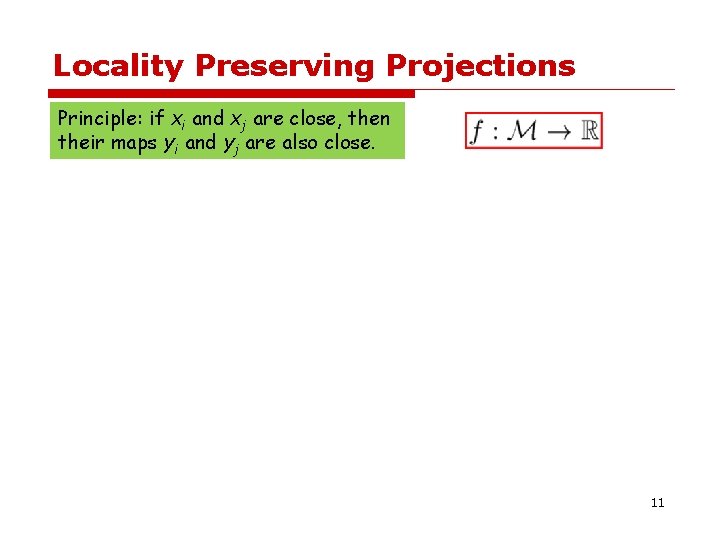
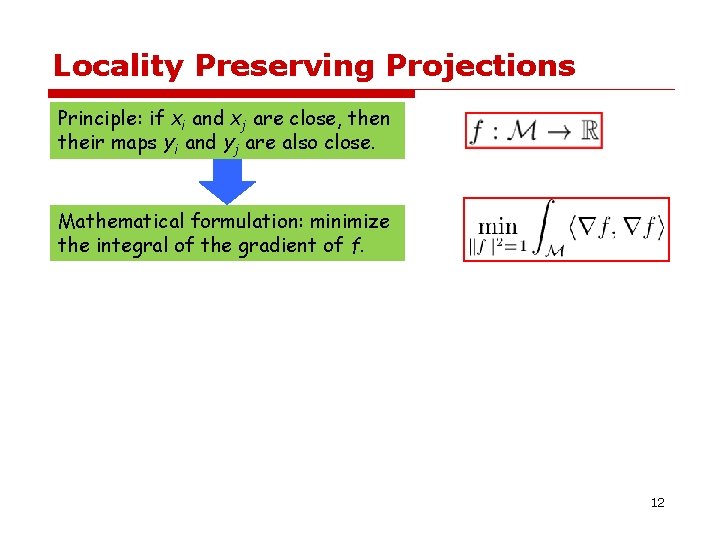
Locality Preserving Projections Principle: if xi and xj are close, then their maps yi and yj are also close. 11

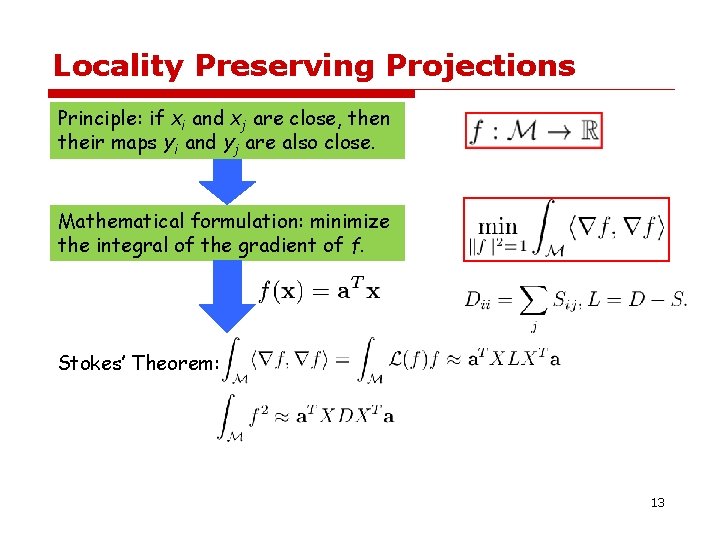
Locality Preserving Projections Principle: if xi and xj are close, then their maps yi and yj are also close. Mathematical formulation: minimize the integral of the gradient of f. 12

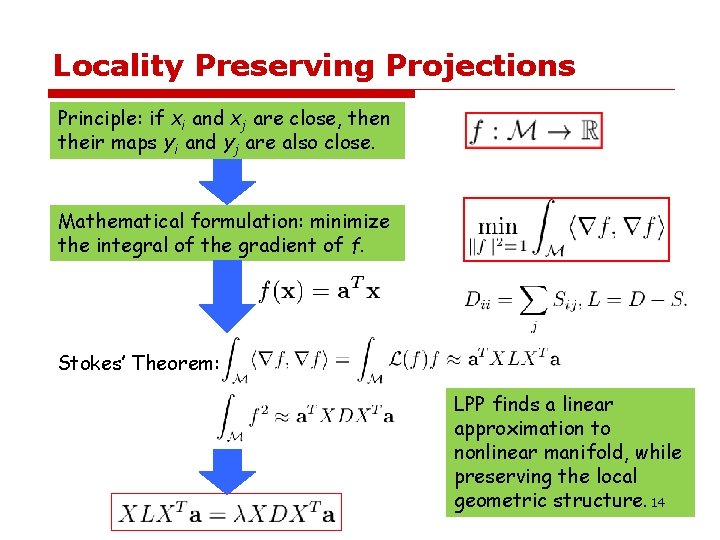
Locality Preserving Projections Principle: if xi and xj are close, then their maps yi and yj are also close. Mathematical formulation: minimize the integral of the gradient of f. Stokes’ Theorem: 13

Locality Preserving Projections Principle: if xi and xj are close, then their maps yi and yj are also close. Mathematical formulation: minimize the integral of the gradient of f. Stokes’ Theorem: LPP finds a linear approximation to nonlinear manifold, while preserving the local geometric structure. 14

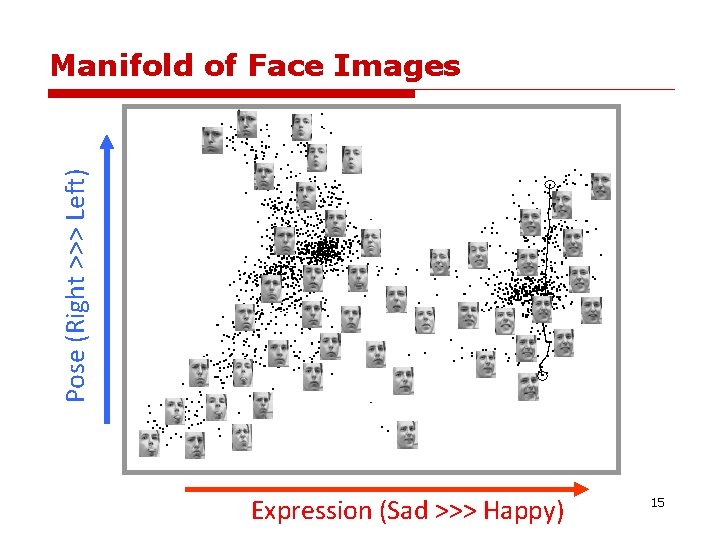
Pose (Right >>> Left) Manifold of Face Images Expression (Sad >>> Happy) 15

Slant Manifold of Handwritten Digits Thickness 16

Active and Semi-Supervised Learning: A Geometric Perspective o Learning target: o Training Examples: o Linear Regression Model 17

Generalization Error o Goal of Regression Obtain a learned function that minimizes the generalization error (expected error for unseen test input points). o Maximum Likelihood Estimate 18

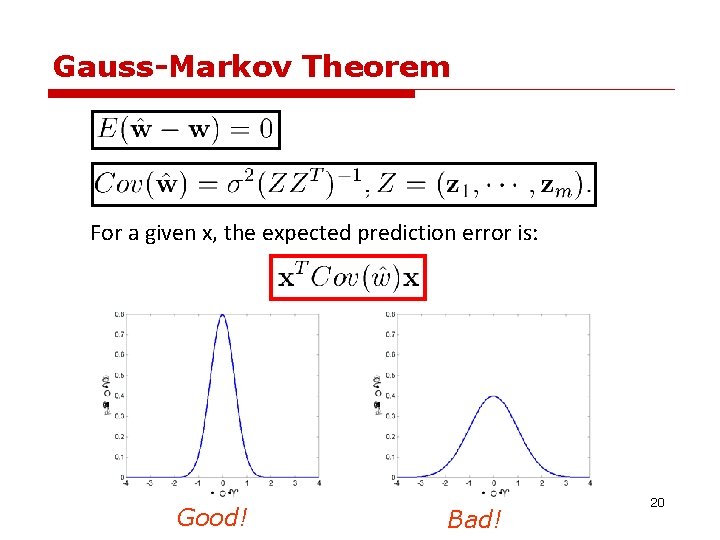
Gauss-Markov Theorem For a given x, the expected prediction error is: 19

Gauss-Markov Theorem For a given x, the expected prediction error is: Good! Bad! 20

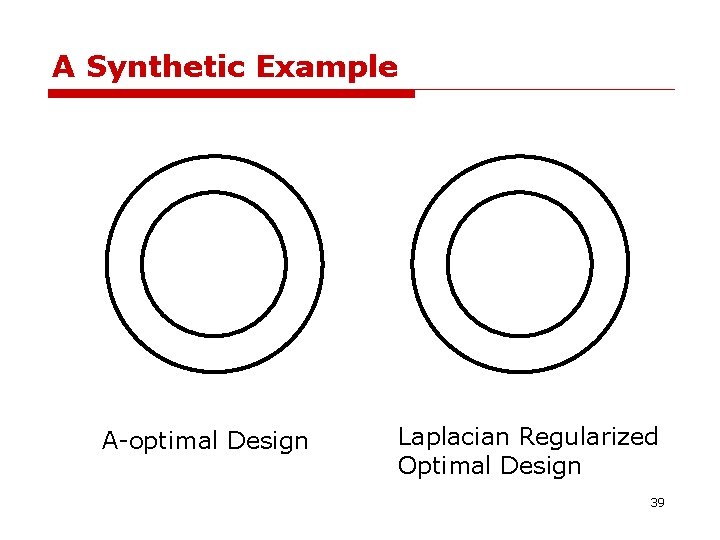
Experimental Design Methods Three most common scalar measures of the size of the parameter (w) covariance matrix: o A-optimal Design: determinant of Cov(w). o D-optimal Design: trace of Cov(w). o E-optimal Design: maximum eigenvalue of Cov(w). Disadvantage: these methods fail to take into account unmeasured (unlabeled) data points. 21

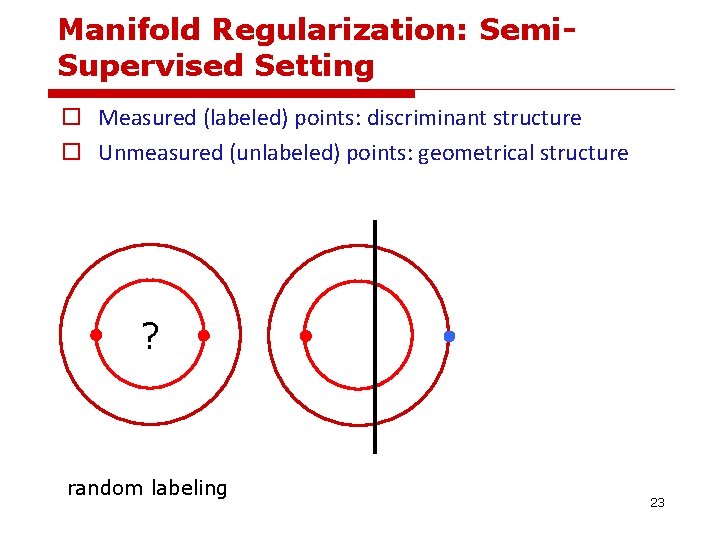
Manifold Regularization: Semi. Supervised Setting o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure ? 22

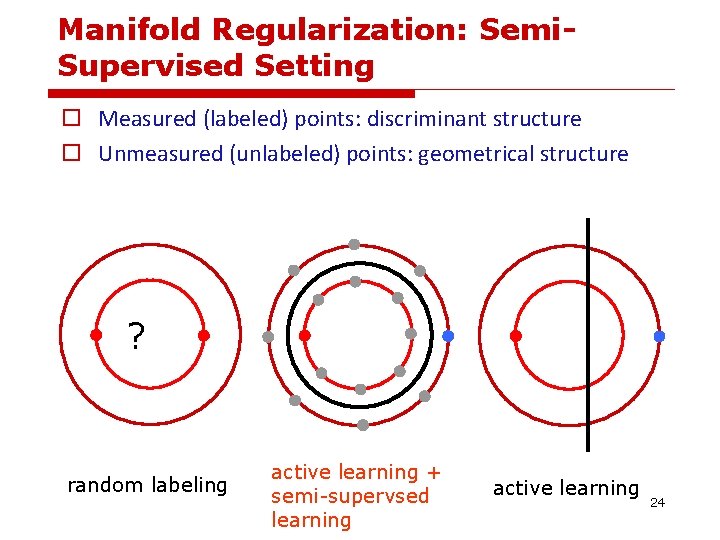
Manifold Regularization: Semi. Supervised Setting o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure ? random labeling 23

Manifold Regularization: Semi. Supervised Setting o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure ? random labeling active learning + semi-supervsed learning active learning 24

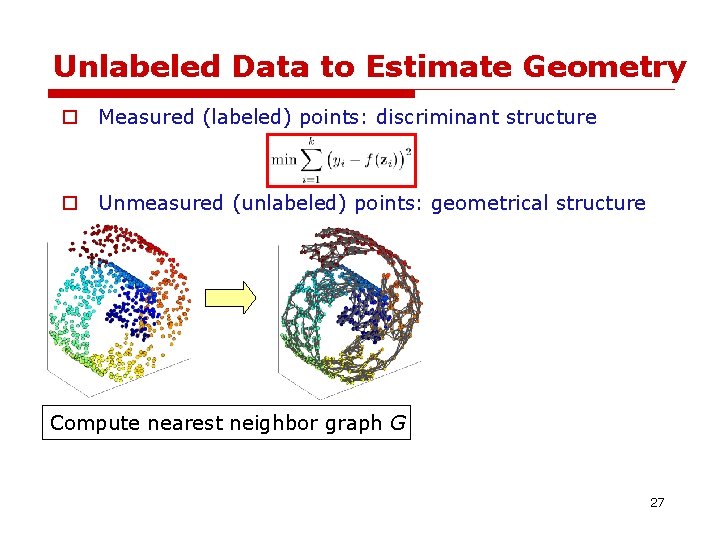
Unlabeled Data to Estimate Geometry o Measured (labeled) points: discriminant structure 25

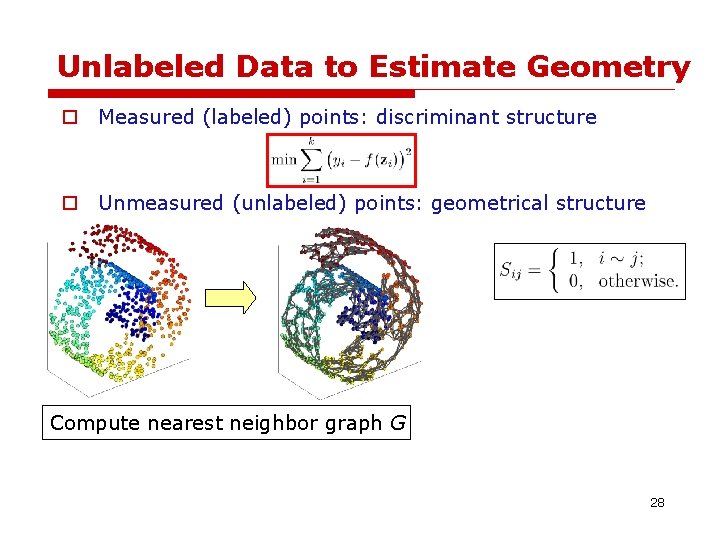
Unlabeled Data to Estimate Geometry o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure 26

Unlabeled Data to Estimate Geometry o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure Compute nearest neighbor graph G 27

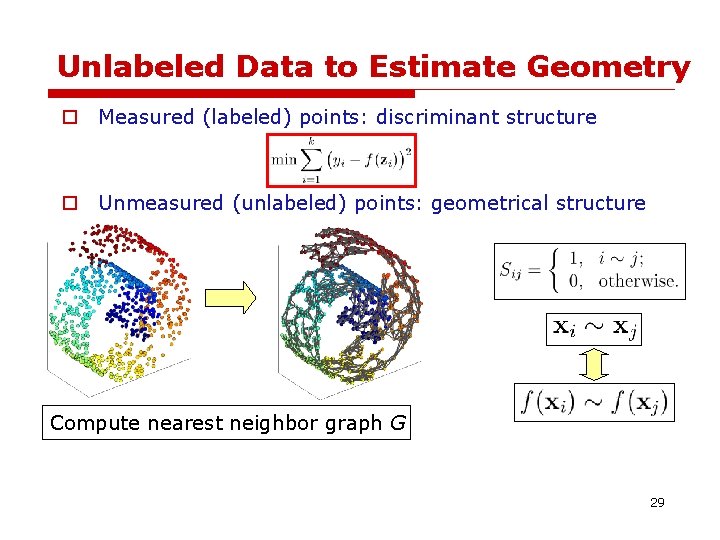
Unlabeled Data to Estimate Geometry o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure Compute nearest neighbor graph G 28

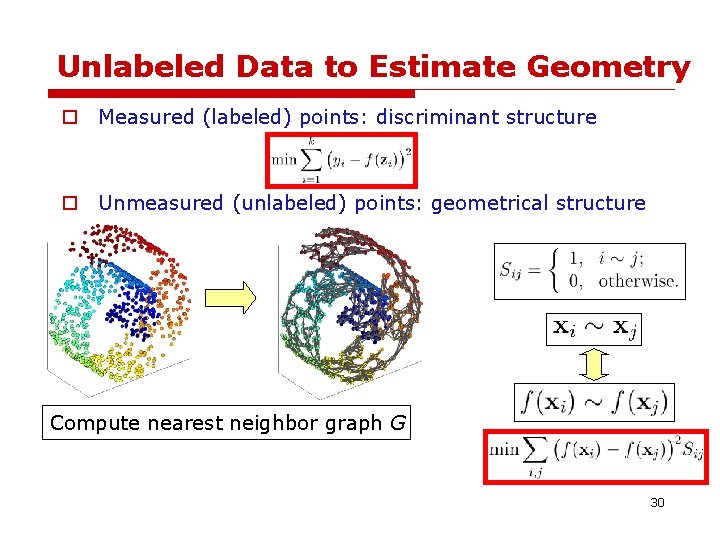
Unlabeled Data to Estimate Geometry o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure Compute nearest neighbor graph G 29

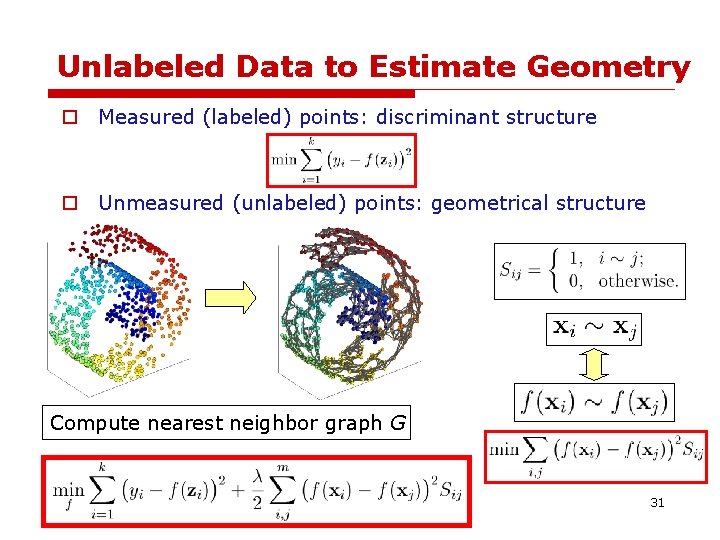
Unlabeled Data to Estimate Geometry o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure Compute nearest neighbor graph G 30

Unlabeled Data to Estimate Geometry o Measured (labeled) points: discriminant structure o Unmeasured (unlabeled) points: geometrical structure Compute nearest neighbor graph G 31

Laplacian Regularized Least Square (Belkin and Niyogi, 2006) o Linear objective function o Solution 32

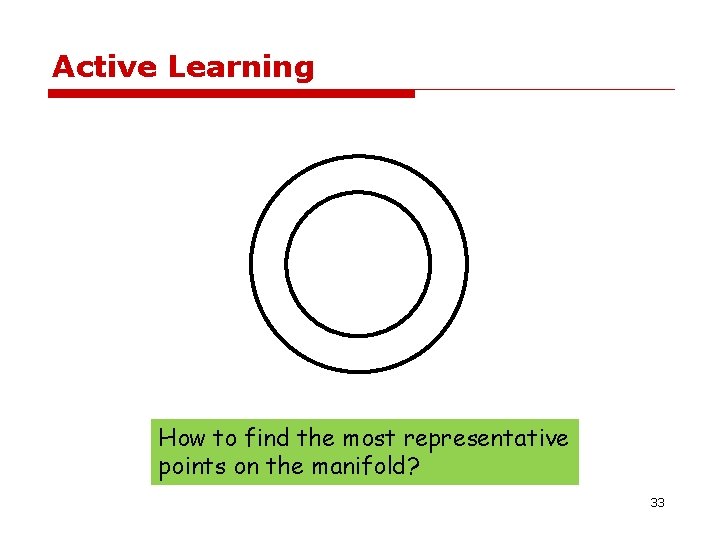
Active Learning How to find the most representative points on the manifold? 33

Active Learning p Objective: Guide the selection of the subset of data points that gives the most amount of information. p Experimental design: select samples to label p Manifold Regularized Experimental Design n Share the same objective function as Laplacian Regularized Least Squares, simultaneously minimize the least square error on the measured samples and preserve the local geometrical structure of the data space. 34

Analysis of Bias and Variance o o , o In order to make the estimator as stable as possible, the size of the covariance matrix should be as small as possible. o D-optimality: minimize the determinant of the covariance matrix 35

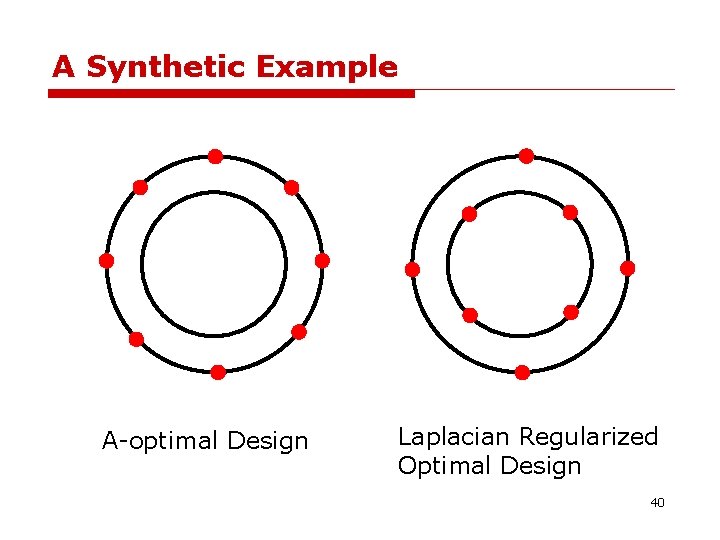
The algorithm Manifold Regularized Experimental Design Where are selected from Select the first data point such that is maximized, Suppose k points have been selected, choose the (k+1)th point such that. Update 36

Nonlinear Generalization in RKHS o Consider feature space F induced by some nonlinear mapping φ, and < f(xi), f(xj) >=K(xi, xi). o K(·, ·): positive semi-definite kernel function o Regression model in RKHS: o Objective function in RKHS: 37

Nonlinear Generalization in RKHS Kernel Graph Regularized Experimental Design where are selected from Select the first data point such that is maximized, Suppose k points have been selected, choose the (k+1)th point such that. Update 38

A Synthetic Example A-optimal Design Laplacian Regularized Optimal Design 39

A Synthetic Example A-optimal Design Laplacian Regularized Optimal Design 40

Application to image/video compression 41

Video compression 42

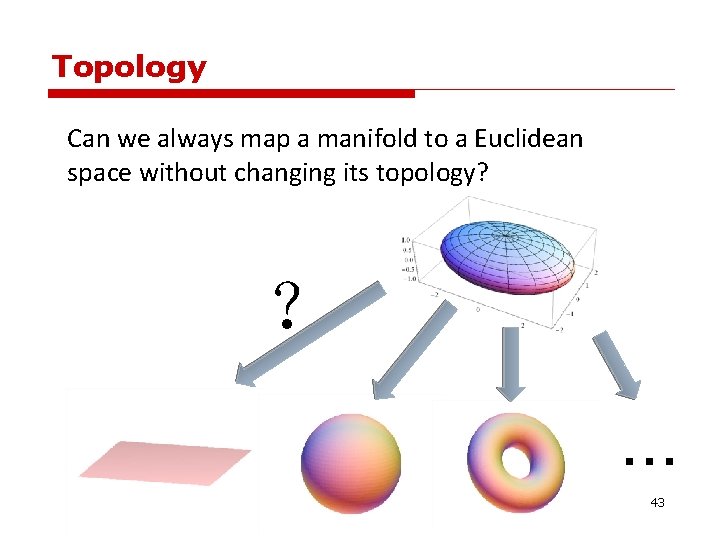
Topology Can we always map a manifold to a Euclidean space without changing its topology? ？ … 43

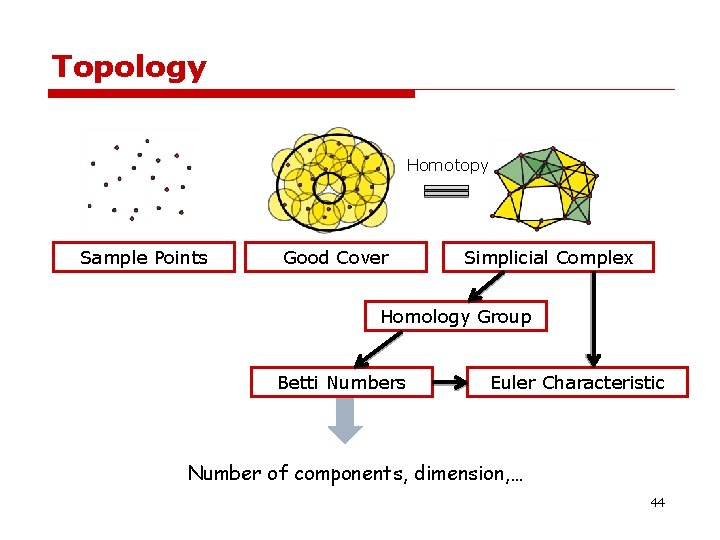
Topology Homotopy Sample Points Good Cover Simplicial Complex Homology Group Betti Numbers Euler Characteristic Number of components, dimension, … 44

Topology The Euler Characteristic is a topological invariant, a number that describes one aspect of a topological space’s shape or structure. 1 0 -2 1 0 2 0 The Euler Characteristic of Euclidean space is 1! 45

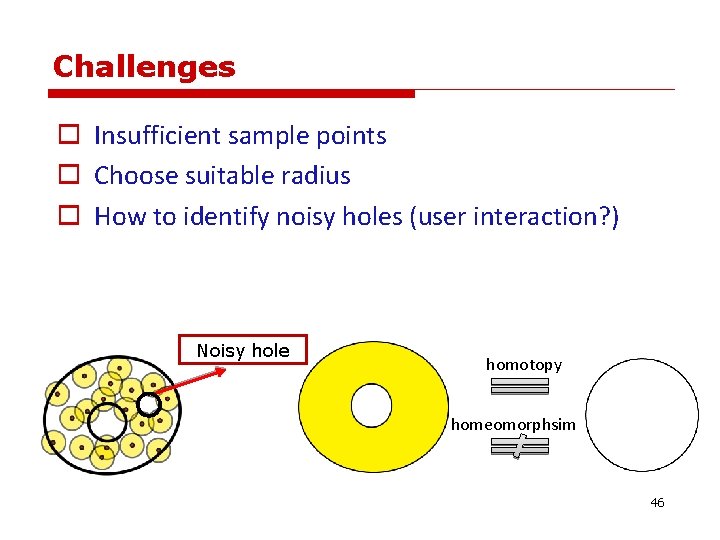
Challenges o Insufficient sample points o Choose suitable radius o How to identify noisy holes (user interaction? ) Noisy hole homotopy homeomorphsim 46

Q&A 47