A Geometric Approach for Partitioning NDimensional NonRectangular Iteration

A Geometric Approach for Partitioning N-Dimensional Non-Rectangular Iteration Spaces Arun Kejariwal Paolo D’Alberto 1 1 Alexandru Nicolau 1 Constantine D. Polychronopoulos 2 1 2 Center for Embedded Computer Systems University of California at Irvine Center for Supercomputing Research and Development University of Illinois at Urbana-Champaign

Outline q Introduction Ø q q Motivation Problem statement Ø Ø q q q 2 Terminology Uniform Partitioning Processor Allocation Our Approach Experimental Results Conclusion

Introduction q Scientific and numerical Applications Ø Ø q Multiprocessor systems Ø q Computation intensive Large amounts of parallelism Exploit parallelism Expose high-level loop parallelism Ø Ø Loop spreading Minimize communication overhead § 3 Minimize the number of processors

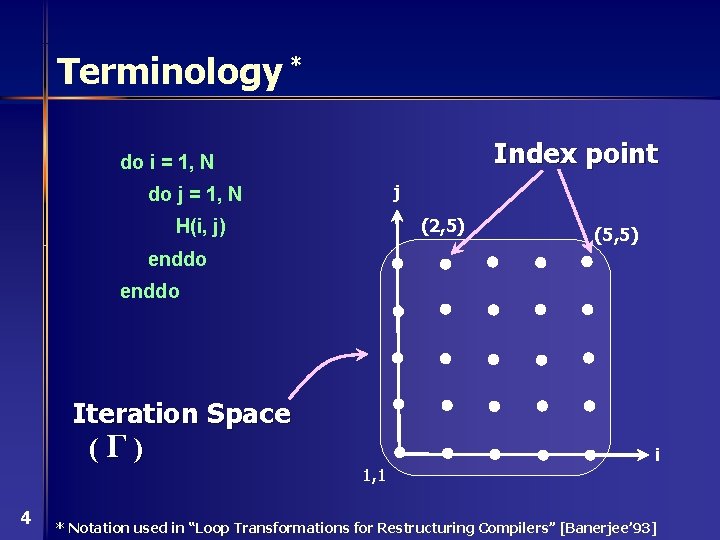
Terminology * Index point do i = 1, N j do j = 1, N (2, 5) H(i, j) (5, 5) enddo Iteration Space (Γ) 4 i 1, 1 * Notation used in “Loop Transformations for Restructuring Compilers” [Banerjee’ 93]

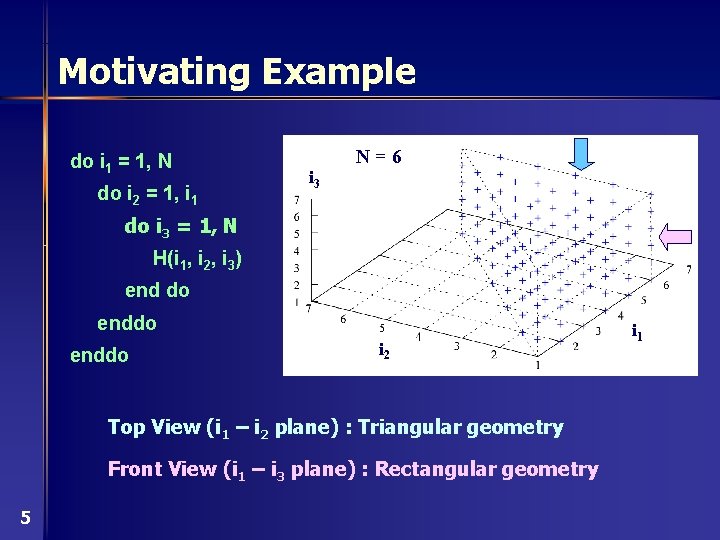
Motivating Example do i 1 = 1, N do i 2 = 1, i 1 N=6 i 3 do i 3 = 1, N H(i 1, i 2, i 3) end do enddo i 2 Top View (i 1 – i 2 plane) : Triangular geometry Front View (i 1 – i 3 plane) : Rectangular geometry 5 i 1

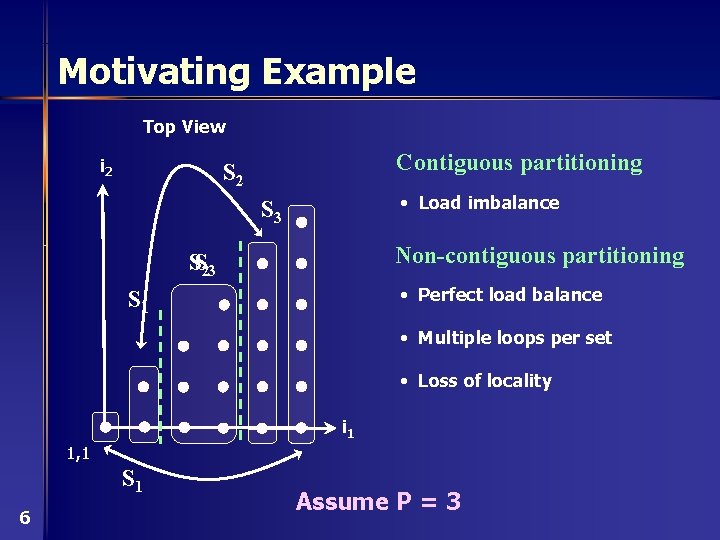
Motivating Example Top View i 2 Contiguous partitioning S 2 • Load imbalance S 3 Non-contiguous partitioning SS 23 • Perfect load balance S 1 • Multiple loops per set • Loss of locality i 1 1, 1 S 1 6 Assume P = 3

Motivating Example Front View Loop permutation-based contiguous partitioning i 3 • Perfect load balance • Remapping of index expressions • Finding a permutation for uniform partitioning is non-trivial 1, 1 7 i 1 Assume P = 3

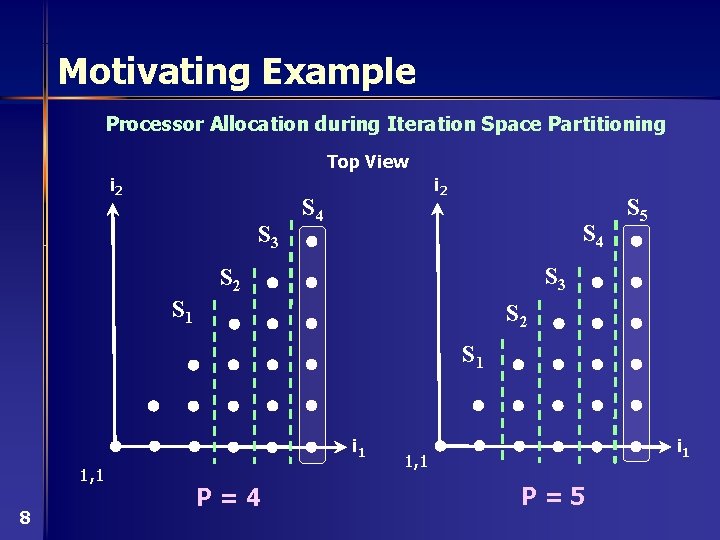
Motivating Example Processor Allocation during Iteration Space Partitioning Top View i 2 S 3 i 2 S 4 S 5 S 3 S 2 S 1 i 1 1, 1 8 P=4 i 1 1, 1 P=5

Previous Work q Cyclic Partitioning § False sharing q Balanced Chunk Scheduling [Haghighat 92] § Restricted to double loops q Canonical loop partitioning [Sakellariou 96] § Non-contiguous partitioning q Communication minimization [Dion 96, Koziris 97] Do not address Processor Allocation 9

Our Model A Perfectly Nested DOALL Loop do i 1 = 1, N, s 1 Non-Rectangular Iteration do i 2 = f 1(i 1), g 1(i 1), s 2 · Spaces · do in = fn-1(i 1, i 2, … , in-1), gn-1(i 1, i 2, … , in-1), sn LOOP BODY enddo · 10 · enddo fr(i 1, i 2, … , ir-1) = ar 0 + ar 1 i 1 + … + ar(r-1)ir-1 gr(i 1, i 2, … , ir-1) = ar 0 + ar 1 i 1 + … + ar(r-1)ir-1 fr ≤ gr

Problem Statement Input : N-dimensional Iteration Space ( Γ ) P processors j 1, 1 P 2 PP N, 1 Outermost i Loop Output : P partitions with “uniform” load 11

Problem Statement I Uniform Partitioning Given: An iteration space Γ and P processors Objective: Find a contiguous partition with uniform load across different processors II Processor Allocation Given : A partition with minimum execution time Objective : Minimize the number of processors for the given partition while maintaining the performance 12

Our Approach Basic Idea q Model the iteration space as a convex polytope q Partition the polytope into sets of equal volumes Ø q Equal volumes Ξ Uniform distribution of index points Each set of the partition is mapped to a different processor. 13

Our Approach 1: Compute the total volume V of Γ k N=7 do i = 1, N do j = 1, i do k = 1, j 7, 7, 7 LOOP BODY 1, 1, 1 j enddo i 14

Our Approach 2: Compute a partial volume V(x) of Γ Each set has equal volume k k P=3 7, 7, 7 1, 1, 1 x 1, 1, 1 j γ 2 i i 3: Determine the breakpoints, γk for 1≤k≤ P-1 15

Our Approach 4: Eliminate void sets i 2 P=5 S 4 S 3 S 2 S 1 i 1 1, 1 16 Eliminate v Minimizes the number of processors v Size of the largest set remains constant

Our Approach 5: Determine loop bounds Given the breakpoints γk , compute lbi , ubi i 2 S 4 S 3 (lb 1 , ub 1) = (1, 3) S 2 (lb 2 , ub 2) = (4, 4) (lb 3 , ub 3) = (5, 5) S 1 17 1, 1 (lb 4 , ub 4) = (6, 6) γ 1 γ 2 γ 3 6, 1 i 1

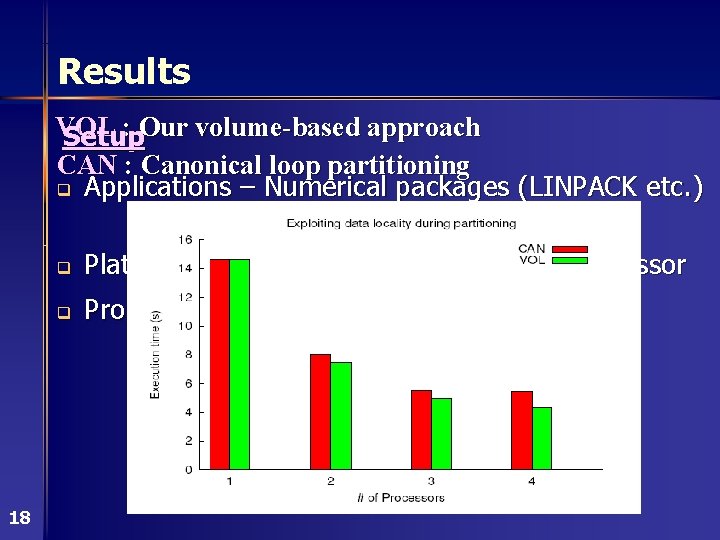
Results VOL : Our volume-based approach Setup CAN : Canonical loop partitioning q Applications – Numerical packages (LINPACK etc. ) and literature 18 q Platform – 4 -way shared-memory multiprocessor q Problem size – N =1000

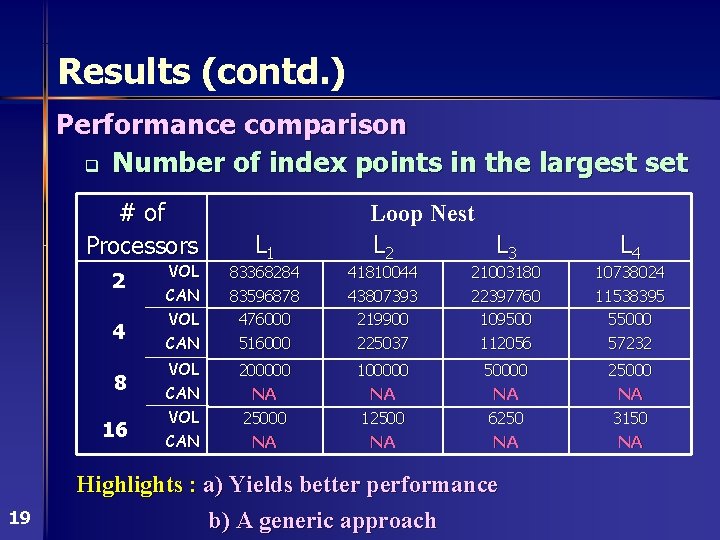
Results (contd. ) Performance comparison q Number of index points in the largest set # of Processors 2 4 8 16 19 L 1 Loop Nest L 2 L 3 L 4 VOL CAN VOL 83368284 83596878 476000 41810044 43807393 219900 21003180 22397760 109500 10738024 11538395 55000 CAN 516000 225037 112056 57232 VOL CAN VOL 200000 NA 25000 100000 NA 12500 50000 NA 6250 25000 NA 3150 CAN NA NA Highlights : a) Yields better performance b) A generic approach

Conclusions n Geometric approach for Iteration Space Partitioning § § n Load balancing Processor Allocation More general than existing techniques Future Work n 20 Run-time Partitioning