A Gentle Tutorial of the EM Algorithm and

A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models Jeff A. Bilmes International Computer Science Institute Berkeley CA, and Computer Science Division Department of Electrical Engineering and Computer Science U. C. Berkeley April 1998 Hsu Ting-Wei ‘s slide Presented by Patty Liu

Outline Abstract Maximum-likelihood Basic EM Finding Maximum Likelihood Mixture Densities Parameters via EM Learning the parameters of an HMM, EM, and the Baum-Welch algorithm 2020/11/24 NTNU Speech Lab 2

Abstract Using Expectation-Maximization (EM) algorithm to solve the maximum-likelihood (ML) parameter estimation problem EM parameter estimation procedure for two applications: Finding the parameters of a mixture of Gaussian densities Finding the parameters of a hidden Markov model (HMM) (i. e. , the Baum. Welch algorithm) for both discrete and Gaussian mixture observation models Trying to emphasize intuition rather than mathematical rigor 2020/11/24 NTNU Speech Lab 3

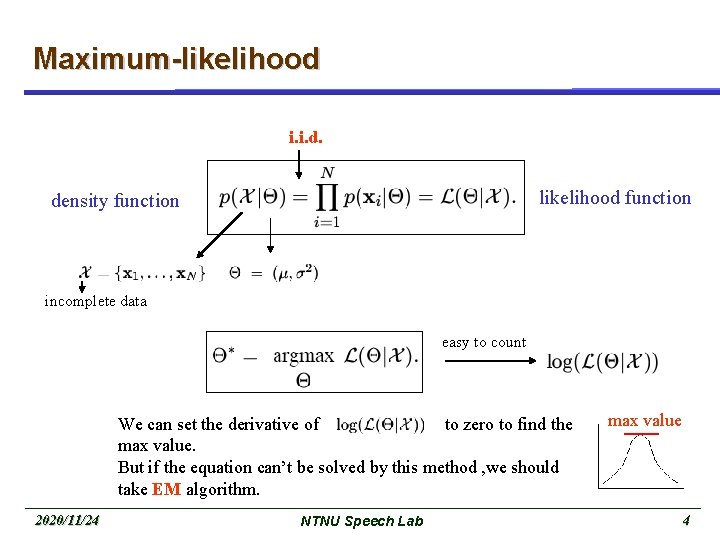
Maximum-likelihood i. i. d. likelihood function density function incomplete data easy to count We can set the derivative of to zero to find the max value. But if the equation can’t be solved by this method , we should take EM algorithm. 2020/11/24 NTNU Speech Lab max value 4

Basic EM Two main applications of the EM algorithm: When the data indeed has missing values, due to problems with or limitations of the observation process. The second occurs when optimizing the likelihood function is analytically intractable but when the likelihood function can be simplified by assuming the existence of and values for additional but missing (or hidden) parameters. more common in the computational pattern recognition community 2020/11/24 NTNU Speech Lab 5

Basic EM (cont. ) complete-data likelihood function joint density function = complete data set observed values missing, unknow values, constant random variable incomplete-data likelihood function : 2020/11/24 NTNU Speech Lab 6

Basic EM (cont. ) The EM algorithm first finds the expected value of the complete-data log-likelihood function E-step : evaluation of expectation new parameter current parameter constant random variable and governed by the distribution Recall : 2020/11/24 space of values NTNU Speech Lab y 7

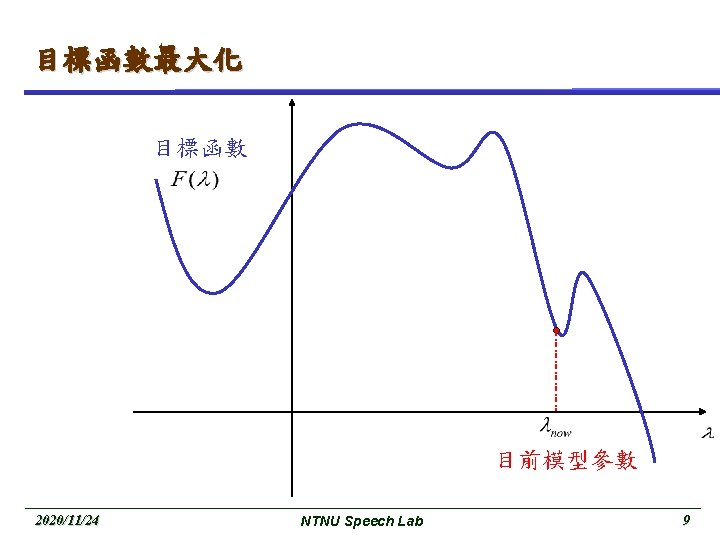
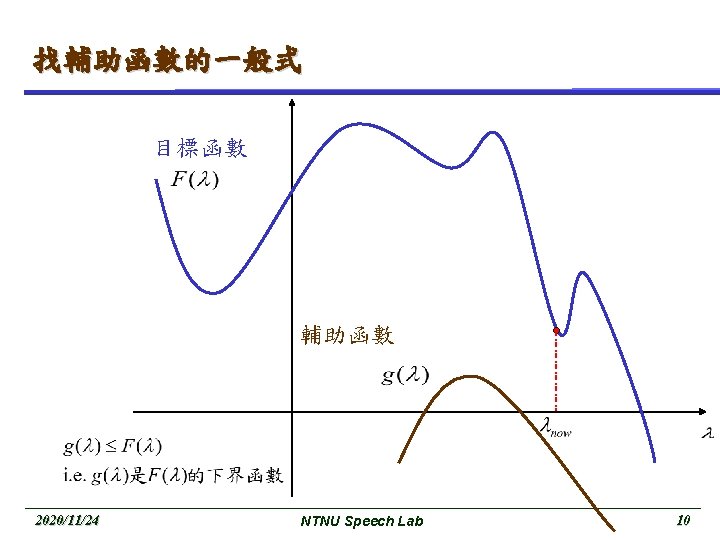
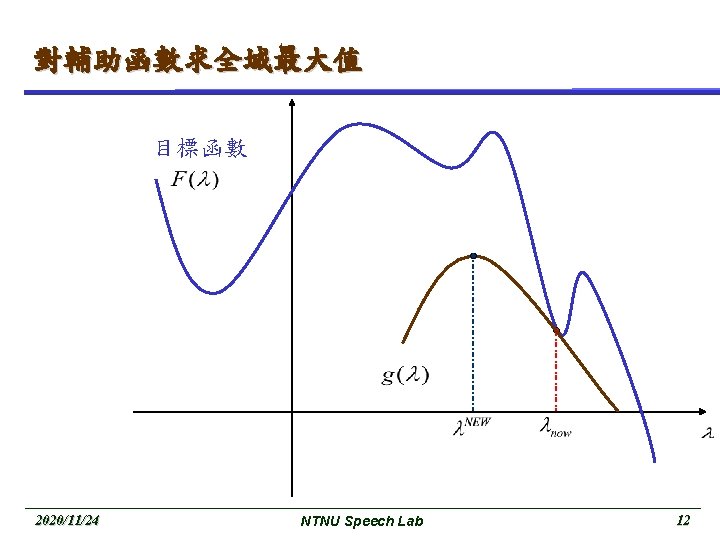
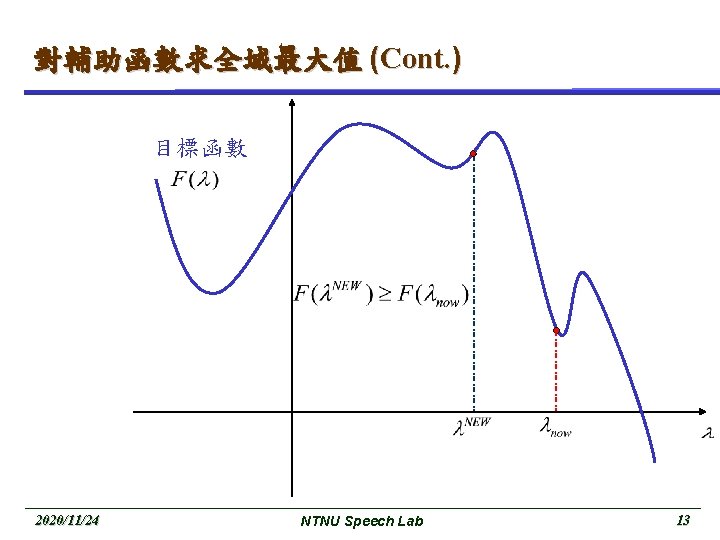
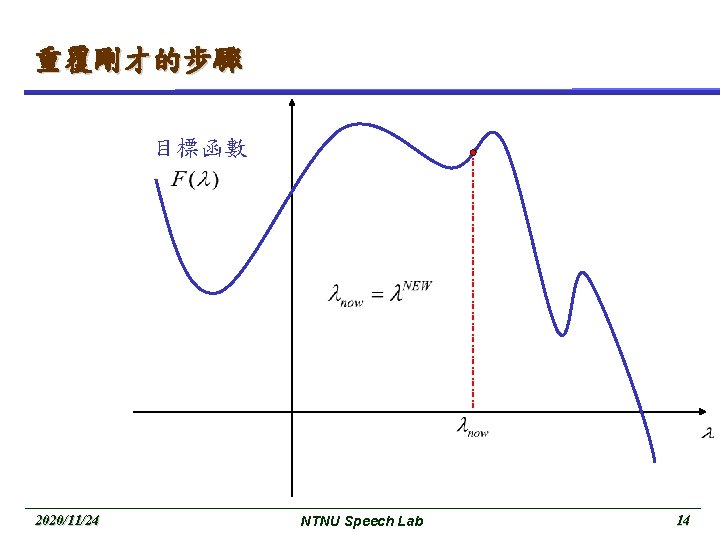
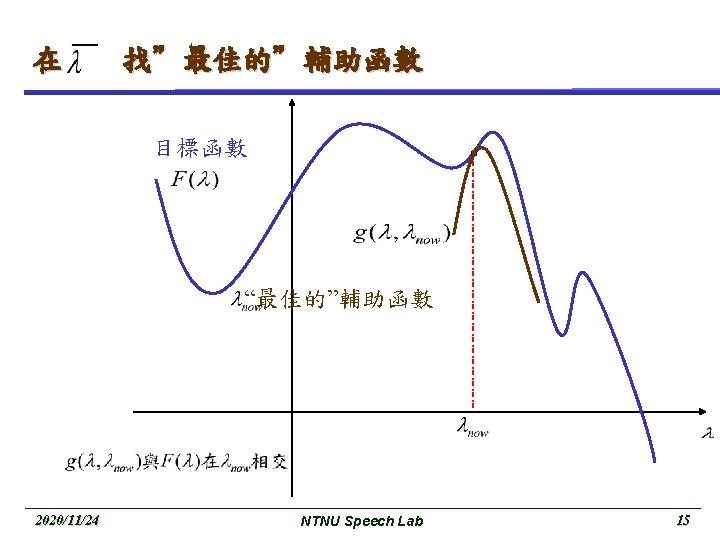
Basic EM (cont. ) M-Step : maximize the expectation These two step are repeated as necessary. Each iteration is guaranteed to increase the log likelihood and the algorithm is guaranteed to converge to a local maximum of the likelihood function. 2020/11/24 NTNU Speech Lab 8

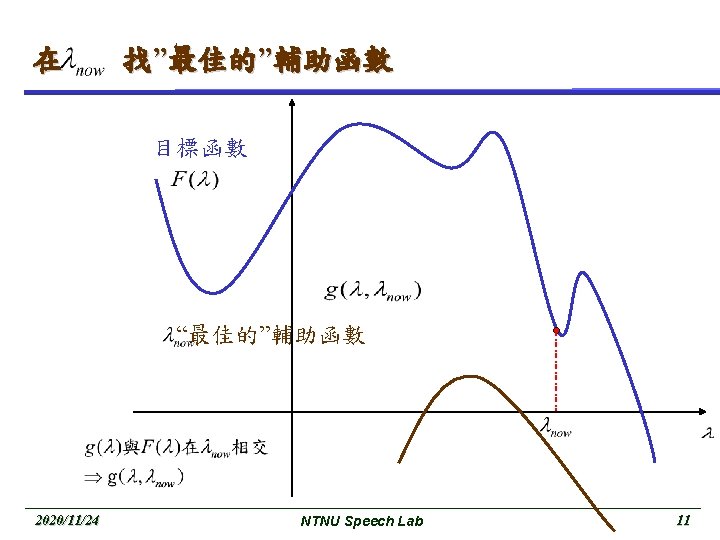
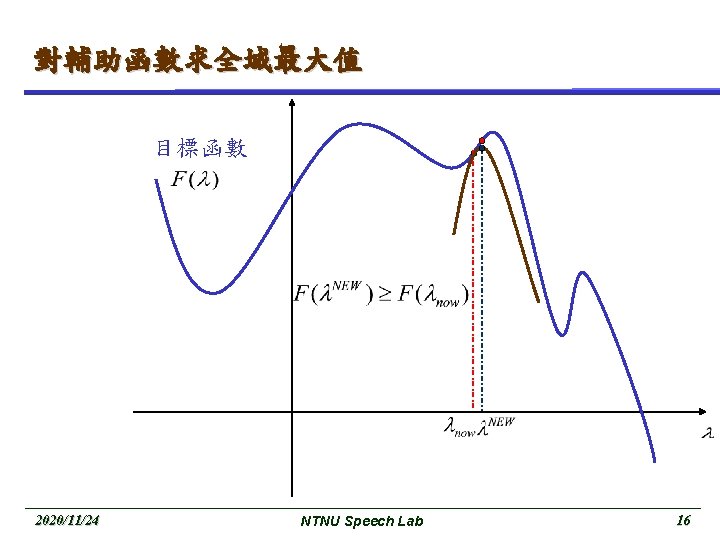
對輔助函數求全域最大值 (Cont. ) 目標函數 2020/11/24 NTNU Speech Lab 13

重覆剛才的步驟 目標函數 2020/11/24 NTNU Speech Lab 14

Finding Maximum Likelihood Mixture Densities Parameters via EM probabilistic model: density function M component densities mixed together with M mixing coefficients . incomplete-data log-likelihood expression : difficult to optimize because it contains the log of the sum. 2020/11/24 NTNU Speech Lab 17

Finding Maximum Likelihood Mixture Densities Parameters via EM (cont. ) If we know the values of y , the likelihood becomes: If we do not know the values of y , and y is a random vector : 2020/11/24 NTNU Speech Lab 18

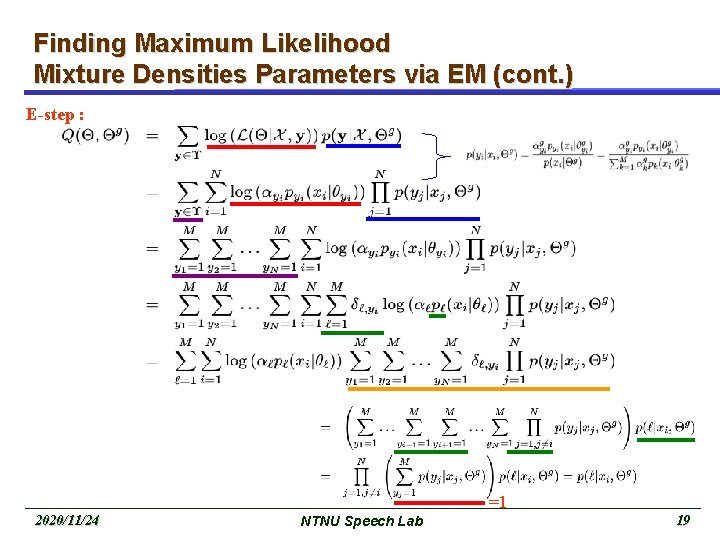
Finding Maximum Likelihood Mixture Densities Parameters via EM (cont. ) E-step : =1 2020/11/24 NTNU Speech Lab 19

Finding Maximum Likelihood Mixture Densities Parameters via EM (cont. ) E-step : M-step: add Lagrange multiplier and 2020/11/24 NTNU Speech Lab 20

Finding Maximum Likelihood Mixture Densities Parameters via EM (cont. ) E-step : M-step: Recall: (*) derivate (*) 將 2020/11/24 代回(*)，整理如下… NTNU Speech Lab 21

Finding Maximum Likelihood Mixture Densities Parameters via EM (cont. ) E-step : M-step: (*) derivate (*) 2020/11/24 NTNU Speech Lab 22

Learning the parameters of an HMM, EM, and the Baum-Welch algorithm A Hidden Markov Model is a probabilistic model of the joint probability of a collection of random variables continuous or discrete observations The model is Two assumption “hidden” and discrete and First-order assumption Output independent assumption Three basic problems 2020/11/24 NTNU Speech Lab 23

Learning the parameters of an HMM, EM, and the Baum-Welch algorithm (cont. ) incomplete-data likelihood function Estimation formula using the Q function. E-step: complete-data likelihood function discrete We know 2020/11/24 NTNU Speech Lab 24

Learning the parameters of an HMM, EM, and the Baum-Welch algorithm (cont. ) M-step in discrete: add Lagrange multiplier and 2020/11/24 NTNU Speech Lab 25

Learning the parameters of an HMM, EM, and the Baum-Welch algorithm (cont. ) M-step in discrete: add Lagrange multiplier and 2020/11/24 NTNU Speech Lab 26

Learning the parameters of an HMM, EM, and the Baum-Welch algorithm (cont. ) M-step in discrete: add Lagrange multiplier and 2020/11/24 NTNU Speech Lab 27

Learning the parameters of an HMM, EM, and the Baum-Welch algorithm (cont. ) M-step in continuous: the mixture component for each state at each time 2020/11/24 NTNU Speech Lab 28