A General EXCEL Solution for LTPD Type Sampling

A General EXCEL Solution for LTPD Type Sampling Plans David C. Trindade, Ph. D. Sun Microsystems David Meade AMD 1999 Joint Statistical Meetings Baltimore, MD

Lot Acceptance Sampling • Assume single random sample of size n from a process or a very large lot. • Binomial distribution is appropriate. • Refer to as type B sampling.

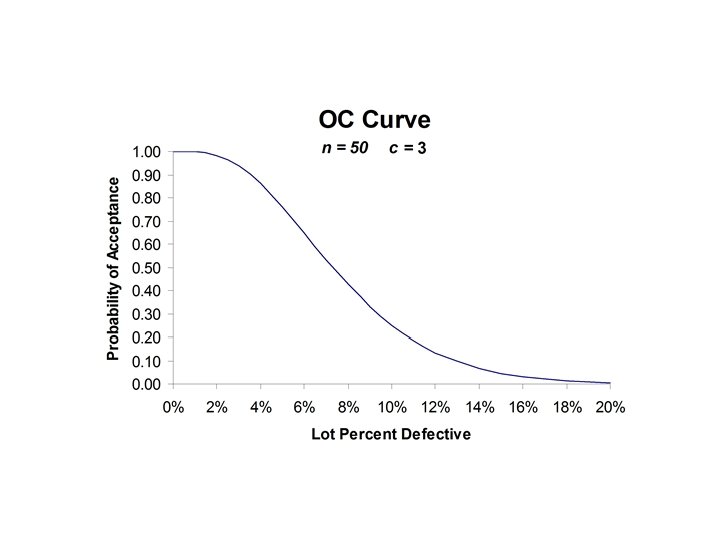
Sampling Plan • Specifies – the sample size n – the acceptance number c • An operating characteristic (OC) curve shows the probability of lot acceptance for a given level of incoming lot percent defective p

LTPD Plans • The quality level at 10% probability of acceptance (consumer’s risk) is called the LTPD. • This rejectable quality level (RQL) is highest percent defective (poorest quality) tolerable in a small percentage of product. • Borderline of distinction between a satisfactory lot and an unsatisfactory one. • LTPD plans are used for many product qualification plans to assure consumer protection.

Common Sampling Problem in Industry • There are constraints on sample size based on limited time, money, or other resources. • There is often the need to adjust sample size and corresponding acceptance number while holding LTPD constant.

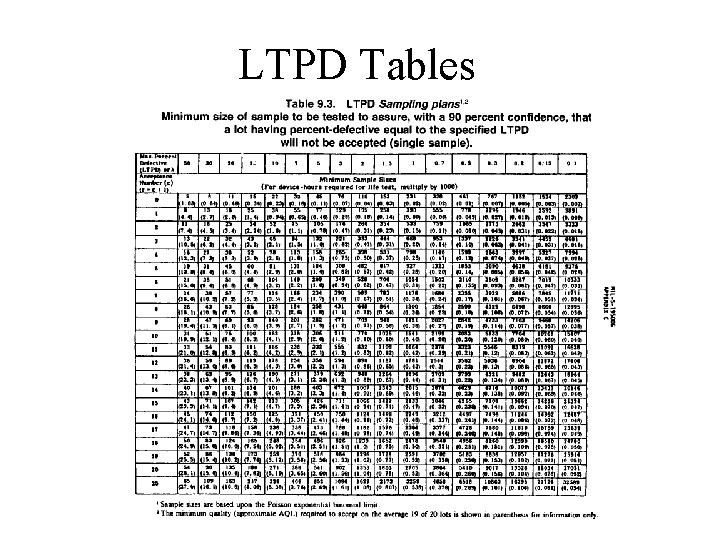
LTPD Tables

Limitations of Tables • LTPD values restricted to only those listed. • There are finite ranges of sample sizes and acceptance numbers.

Example Case • Reliability qualification plan for integrated circuits calls for stressing a sample of 300 units for 1000 hours. Pass requirement is no more than three failures. • Early samples are precious, costing approximately $10, 000 each and are needed for other evaluations. • How can the engineer reduce the sample size and allowed failures while holding the LTPD constant?

Approaches by Engineer • First, the LTPD value must be determined. • Then, LTPD tables may be consulted to see if n = 300 and c = 3 are tabulated. • Approximation may be necessary: – Checking LTPD table, we see n = 333 and c = 3 for LTPD = 2%. – For c = 1, LTPD = 2%, we need n = 195.

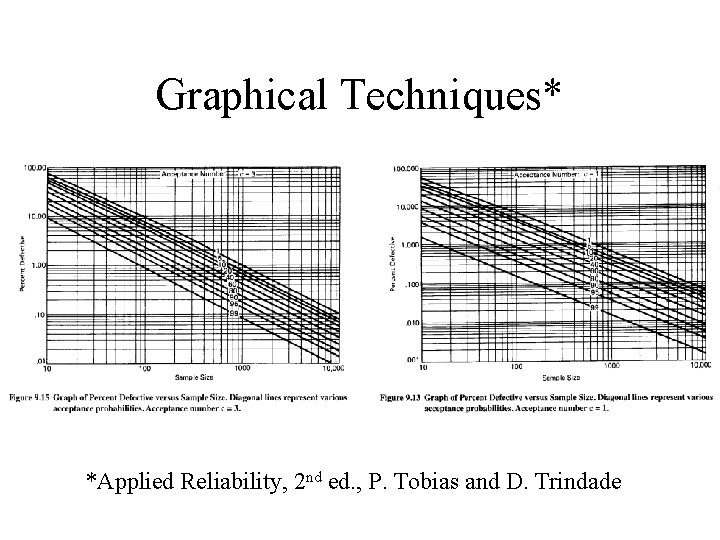
Graphical Techniques* *Applied Reliability, 2 nd ed. , P. Tobias and D. Trindade

Graphical Results • For n = 300, c = 3, LTPD = 2. 2%. • For LTPD = 2. 2%, c = 1, n ~ 180. There is a limitation in these graphs to only c = 0, 1, 2, or 3.

EXCEL Solution (Add-In)

Find LTPD for Given Sampling Plan

Find LTPD for a Given sampling Plan: Output

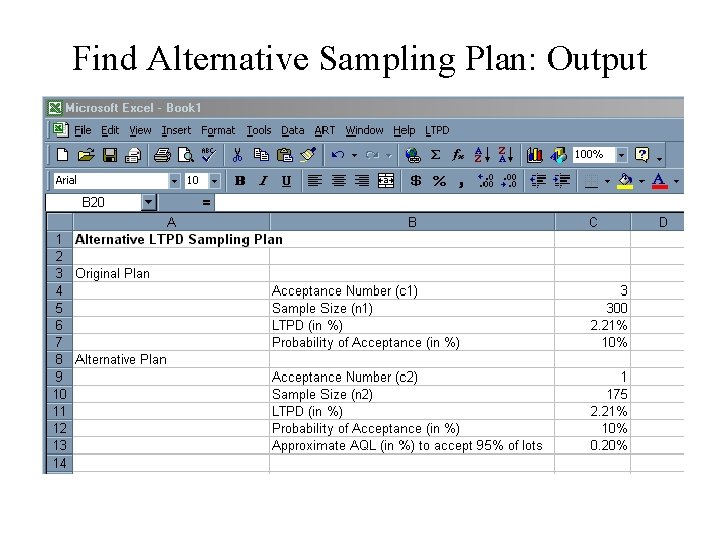
Find Alternative LTPD Sampling Plan

Find Alternative Sampling Plan: Output

Find Sample Size for Given c

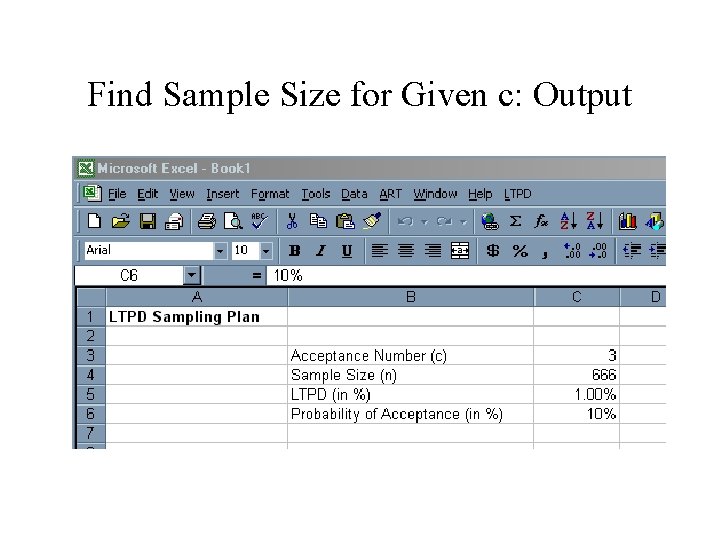
Find Sample Size for Given c: Output

Final Comments • Description and theory presented in paper. • LTPD add-in and paper available for download from www. trindade. com/LTPD. html • Questions to: – david. trindade@eng. sun. com – david. meade@amd. com (VB programming)