A function fx is defined as fx 8

• A function f(x) is defined as f(x) = − 8 x 2. What is f(− 3)? A. − 72 B. 72 C. 192 D. − 576 E. 576 5. 1. 2: Transformations As Functions Do Now 1

5. 1. 2: Transformations As Functions Good things!!!! 2

Note Taking 1. How do you translate a pre-image by changing the function? 2. How do you reflect a figure over an axis? 5. 1. 2: Transformations As Functions • Today’s Date: 9/7 • Essential Questions 3

• • Intro to transformations Define isometric transformations Translations Reflections Guided practice Exit Ticket + group check for understanding Problem Based Task 5. 1. 2: Transformations As Functions Agenda 4

Introduction The word transform means “to change. ” A transformation changes the position, shape, or size of a figure on a coordinate plane. The preimage is the original image It is changed or moved though a transformation, and the resulting figure is called an image 5 5. 1. 2: Transformations As Functions

Introduction Today will be focus on two transformations: Also known as a 1. Translations - slide “rigid 2. Reflections – mirror image transformation” These transformations are examples of isometry, meaning the new image is congruent to the preimage Figures are congruent if they both have the same shape, size, lines, and angles. The new image is simply moving to a new location. 6 5. 1. 2: Transformations As Functions

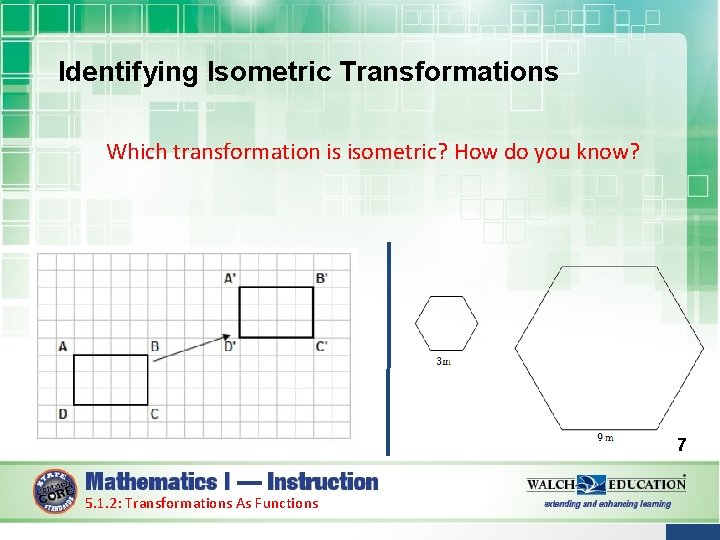
Identifying Isometric Transformations Which transformation is isometric? How do you know? 7 5. 1. 2: Transformations As Functions

Transformations as functions A function is a relationship between two sets of data Each input has exactly one output We can define points of a shape as functions because for each x, we only have one y 8 5. 1. 2: Transformations As Functions

Transformations as Functions, continued In the coordinate plane we define each coordinate, or point, in the form (x, y) The potential inputs for a transformation function f in the coordinate plane will be a real number coordinate pair, (x, y) Each output will be a real number coordinate pair, f (x, y) 9 5. 1. 2: Transformations As Functions

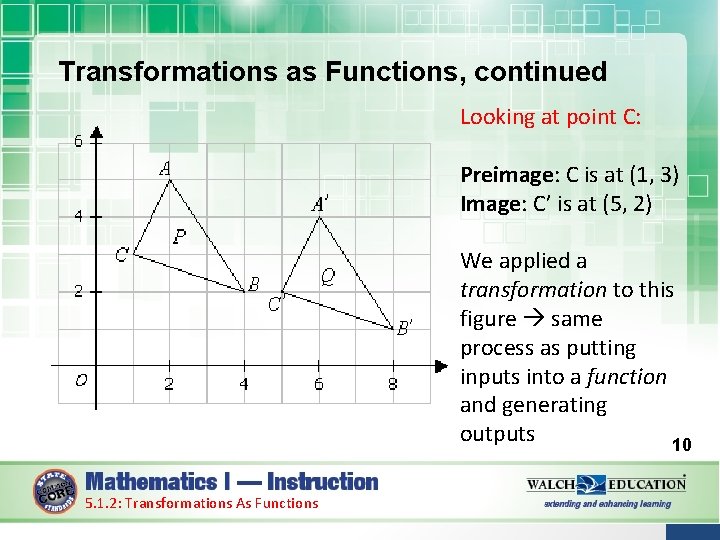
Transformations as Functions, continued Looking at point C: Preimage: C is at (1, 3) Image: C’ is at (5, 2) We applied a transformation to this figure same process as putting inputs into a function and generating outputs 10 5. 1. 2: Transformations As Functions

Transformations as Functions, continued Transformations are generally applied to a set of points on a figure In geometry, these figures are described by points, P, rather than coordinates (x, y) Transformation functions are often given the letters R, S, or T. T(x, y) or T(P) = Transformation on coordinates (x, y) or point P P’ = “P prime” A transformation T on a point P is a function where T(P) is P'. When a transformation is applied to a set of points, such as a triangle, then all points are moved according to the transformation. 11 5. 1. 2: Transformations As Functions

Introduction, continued For example, if T(x, y) = (x + h, y + k), then would be: ALWAYS MOVE X FIRST We move the “x” by positive h, and the “y” by positive k 5. 1. 2: Transformations As Functions 12

Translations Translation = To move something The figure does not change size, shape, or direction – it is simply being moved from one place to another 13 5. 1. 2: Transformations As Functions

Translations Represented by addition and subtraction If we have a point (x, y), we can translate it “up 10 points” and “to the right 20 points” through the translation (x, y) (x+20, y+10) This tells us “all the x units moved by positive 20 and all the y units moved by positive 10 units” 14 5. 1. 2: Transformations As Functions

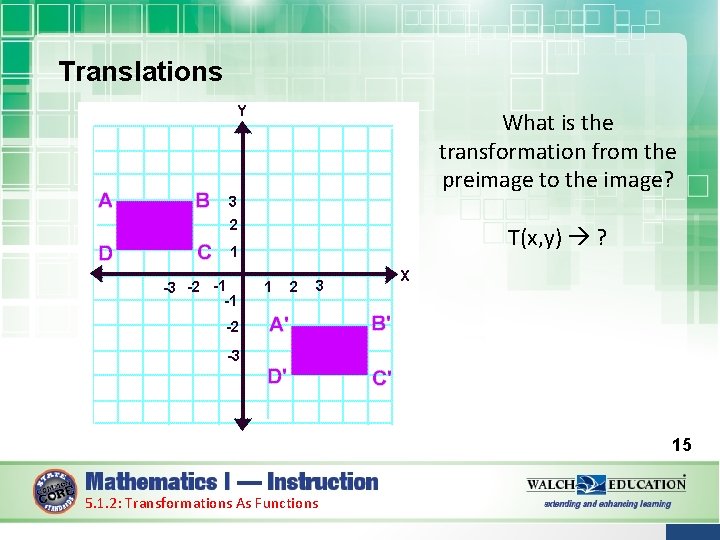
Translations What is the transformation from the preimage to the image? T(x, y) ? 15 5. 1. 2: Transformations As Functions

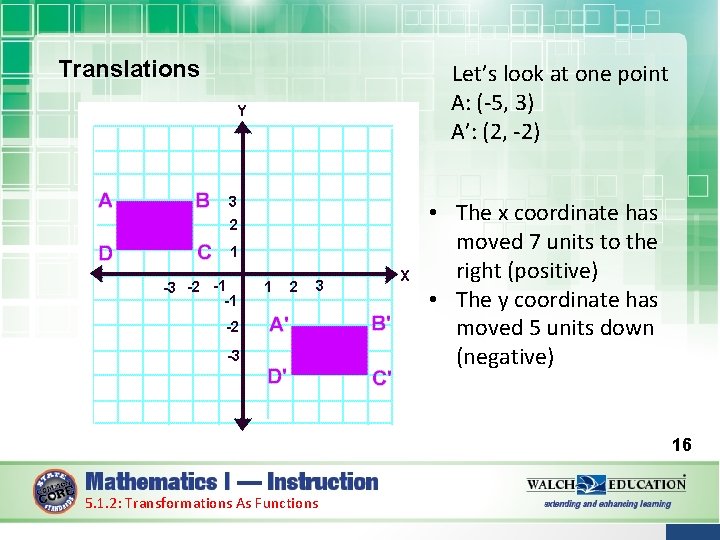
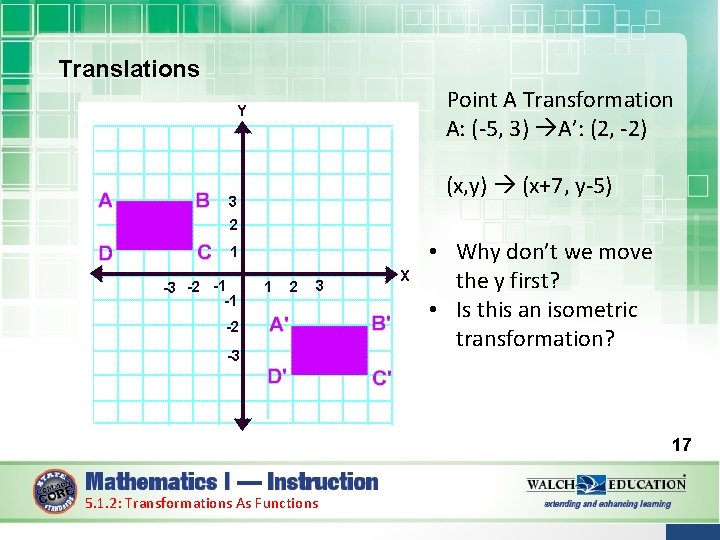
Translations Let’s look at one point A: (-5, 3) A’: (2, -2) • The x coordinate has moved 7 units to the right (positive) • The y coordinate has moved 5 units down (negative) 16 5. 1. 2: Transformations As Functions

Translations Point A Transformation A: (-5, 3) A’: (2, -2) (x, y) (x+7, y-5) • Why don’t we move the y first? • Is this an isometric transformation? 17 5. 1. 2: Transformations As Functions

Translations – quick practice -You can translate a figure without seeing the image Point A: (3, 5) Point B: (5, 5) Point C: (4, 7) Apply the transformation T(x, y) = (x-3, y+6) 18 5. 1. 2: Transformations As Functions

BRAIN BREAK!!!!!!! Find a reason why each one does not belong in the set. 19 5. 1. 2: Transformations As Functions

Reflections Mirror image over an axis 20 5. 1. 2: Transformations As Functions

Reflections The reflected image is always the same size, it is just facing a different direction. Is this an isometric transformation? Why or why not? 21 5. 1. 2: Transformations As Functions

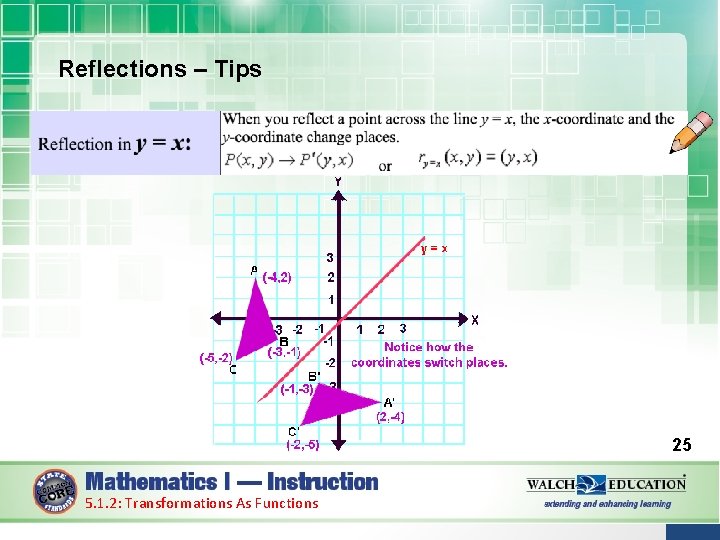
Reflections For today, we will only focus on reflections across: 1. X-axis 2. Y-axis 3. Y = x 22 5. 1. 2: Transformations As Functions

Reflections - Tips When reflecting across the x-axis… WHY DOES THIS MAKE SENSE? ? If I want to reflect the point (9, 14) over the x-axis, what will my new coordinates be? 5. 1. 2: Transformations As Functions 23

Reflections – Tips If I want to reflect the point (9, 14) over the y-axis, what will my new coordinates be? 24 5. 1. 2: Transformations As Functions

Reflections – Tips 25 5. 1. 2: Transformations As Functions

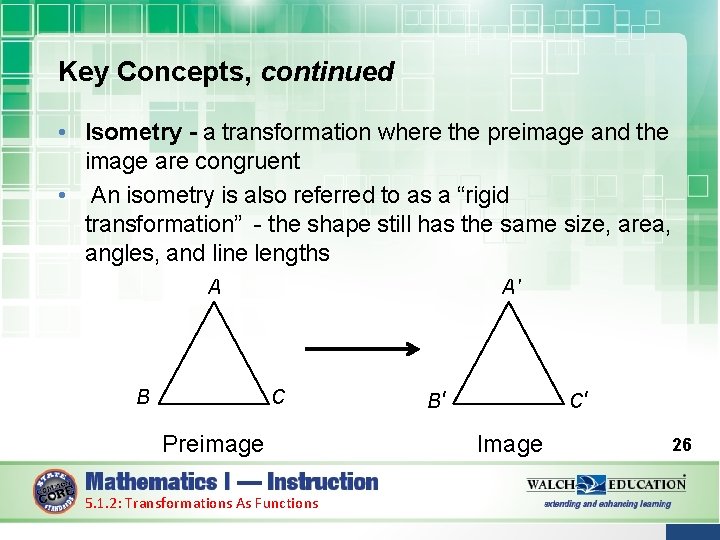
Key Concepts, continued • Isometry - a transformation where the preimage and the image are congruent • An isometry is also referred to as a “rigid transformation” - the shape still has the same size, area, angles, and line lengths A B A' C Preimage 5. 1. 2: Transformations As Functions B' C' Image 26

Guided Practice Example 1 Given the point P(5, 3) and T(2, 2) = (x + 2, y + 2), what are the coordinates of T(P) – also known as P’? 27 5. 1. 2: Transformations As Functions

Guided Practice Example 2 Given the transformation of a translation T(5, -3) = (x+5, y -3), and the points P (– 2, 1) and Q (4, 1), show that the transformation is isometric by calculating the distances, or lengths, of and. 28 5. 1. 2: Transformations As Functions

Guided Practice: Example 3, continued 1. Plot the points of the preimage. 29 5. 1. 2: Transformations As Functions

Guided Practice: Example 3, continued 2. Transform the points. T 5, – 3(x, y) = (x + 5, y – 3) 30 5. 1. 2: Transformations As Functions

Guided Practice: Example 3, continued 3. Plot the image points. 31 5. 1. 2: Transformations As Functions

Guided Practice: Example 3, continued 4. Calculate the distance, d, of each segment from the preimage and the image and compare them. Since the line segments are horizontal, count the number of units the segment spans to determine the distance. The distances of the segments are the same. The translation of the segment is isometric. ✔ 32 5. 1. 2: Transformations As Functions

Exit Ticket 1. True or False: Under the translation (x, y) (x+3, y+2), the point (2, 5) will become (5, 7) 2. Reflect the point (6, 8) over the x-axis. What is your new point? 3. You have a triangle with vertices A, B, C. 1. A is at (-5, 4) 2. B is at (-2, 4) 3. C is at (-2, 2) Apply transformation: T(6, -2) List new vertices A’, B’, C’ 5. 1. 2: Transformations As Functions 33

Problem Based Task (p. 43) “The mail room at a growing retail company stuffs, addresses, weighs, and stamps hundreds of envelopes to be mailed each day. ” 34 5. 1. 2: Transformations As Functions

35 5. 1. 2: Transformations As Functions