A Fully Polynomial Time Approximation Scheme for Timing

A Fully Polynomial Time Approximation Scheme for Timing Driven Minimum Cost Buffer Insertion Shiyan Hu*, Zhuo Li**, Charles Alpert** *Dept of Electrical and Computer Engineering Michigan Technological University **IBM Austin Research Lab Austin, TX

Outline Introduction Previous Works The Algorithm • Timing-cost approximate dynamic programming • Double-ɛ geometric sequence based oracle search Experimental Results Conclusion 2

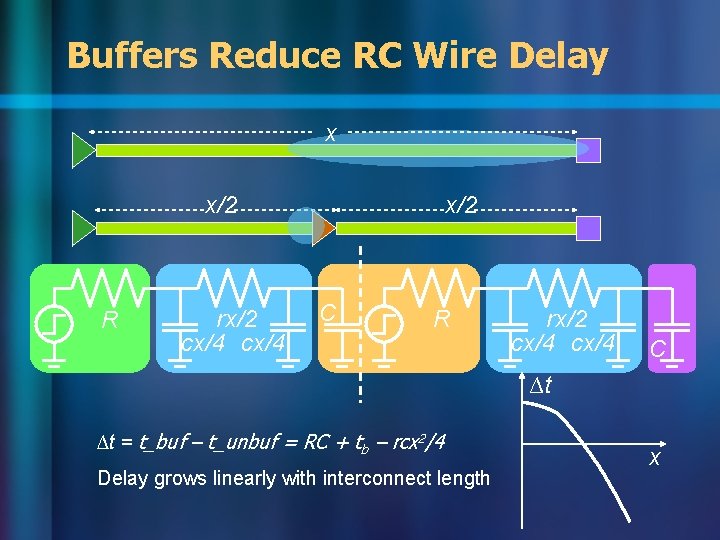
Interconnect Delay Dominates Delay (psec) 300 250 Interconnect delay 200 150 100 Transistor/Gate delay 50 0 0. 8 25. 18. 15. 0. 35 0. 25 0 0 0 Technology generation ( m) 0. 5 3

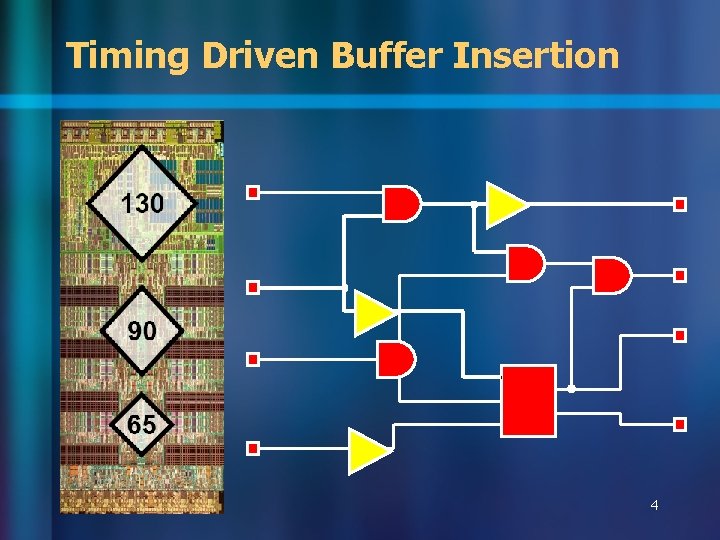
Timing Driven Buffer Insertion 4

Buffers Reduce RC Wire Delay x x/2 R rx/2 cx/4 x/2 C R rx/2 cx/4 C ∆t ∆t = t_buf – t_unbuf = RC + tb – rcx 2/4 Delay grows linearly with interconnect length x

25% Gates are Buffers Saxena, et al. [TCAD 2004] 6

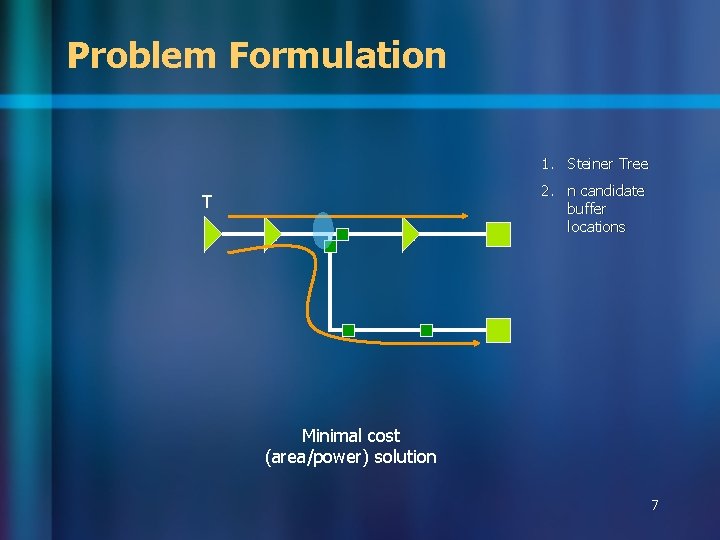
Problem Formulation 1. Steiner Tree 2. n candidate buffer locations T Minimal cost (area/power) solution 7

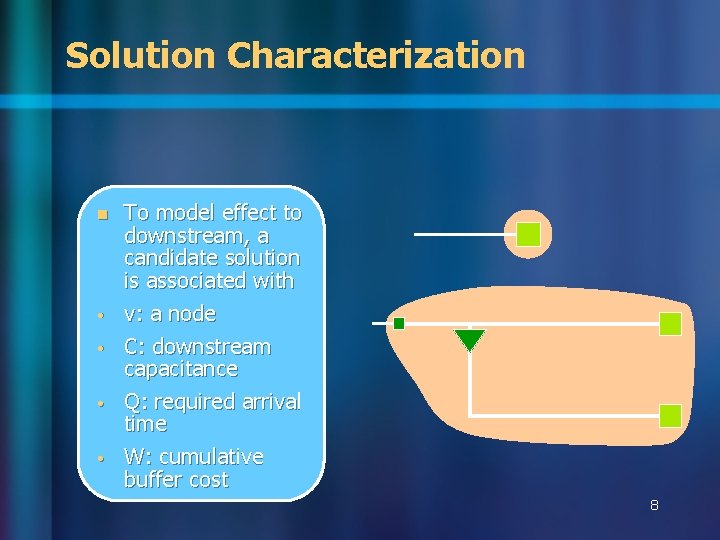
Solution Characterization n • • To model effect to downstream, a candidate solution is associated with v: a node C: downstream capacitance Q: required arrival time W: cumulative buffer cost 8

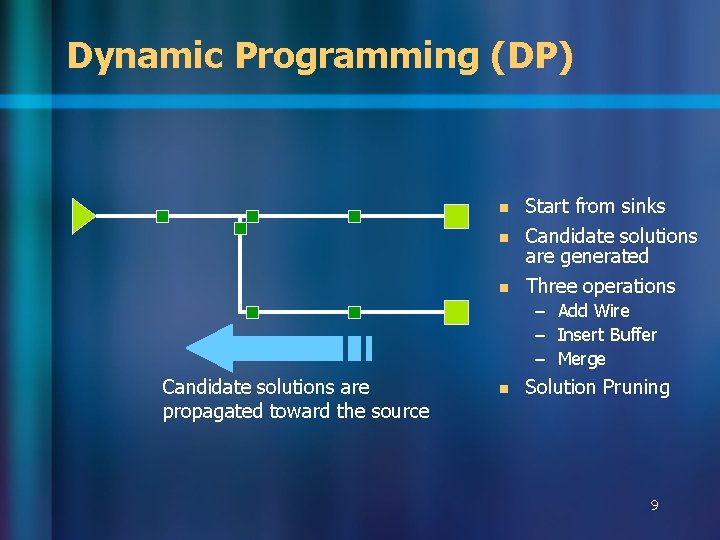
Dynamic Programming (DP) n Start from sinks n Candidate solutions are generated Three operations n – Add Wire – Insert Buffer – Merge Candidate solutions are propagated toward the source n Solution Pruning 9

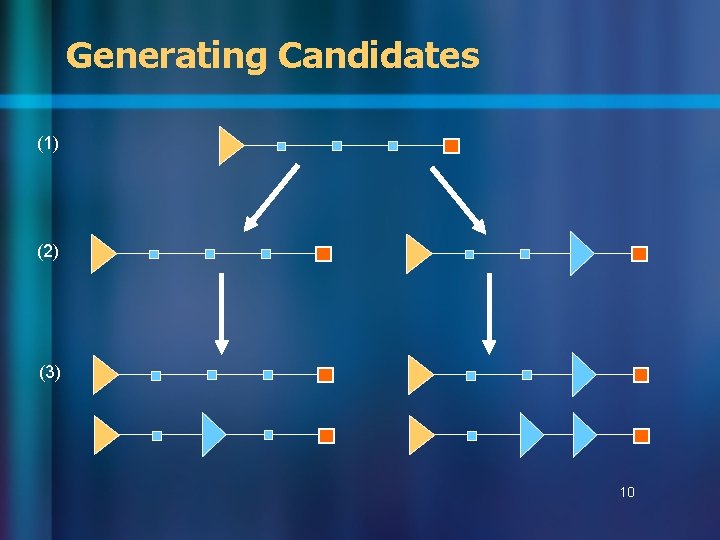
Generating Candidates (1) (2) (3) 10

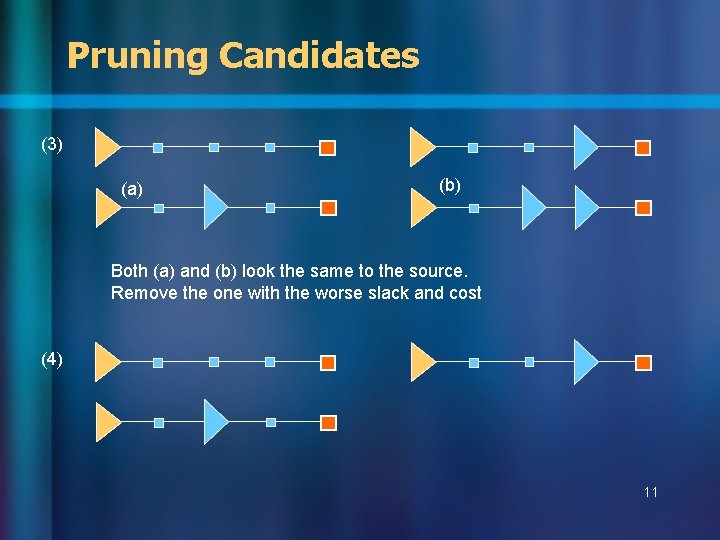
Pruning Candidates (3) (a) (b) Both (a) and (b) look the same to the source. Remove the one with the worse slack and cost (4) 11

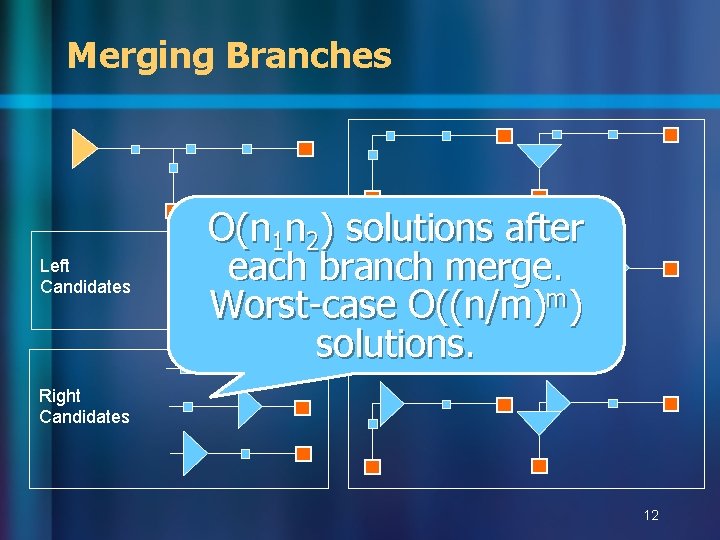
Merging Branches Left Candidates O(n 1 n 2) solutions after each branch merge. Worst-case O((n/m)m) solutions. Right Candidates 12

DP Properties (Q 1, C 1, W 1) inferior/dominated if C 1 C 2, W 1 W 2 Non-dominated solutions are 1 Q 2 maintained - for the same Q and. QW, pick min C n # solutions depends on # of distinct W and Q, but not their values n (Q 2, C 2, W 2) 13

Gi nn ek en ’s al go rit hm 1990 1991 ……. 1996 ……. Li ’s al go rit an hm d Zh ou N P’s ha al go rd ne rit ss hm pr oo f Ch en Sh ia nd Li llis ’a lg or ith m va n Previous Works 2003 2004 ……. 2008 2009 14

Bridging The Gap A Fully Polynomial Time Approximation Scheme (FPTAS) • Provably good • Within (1+ɛ) optimal cost for any ɛ>0 • Runs in time polynomial in n (nodes), b (buffer types) and 1/ɛ • Best solution for an NP-hard problem in theory • Highly practical n We are bridging the gap! 15

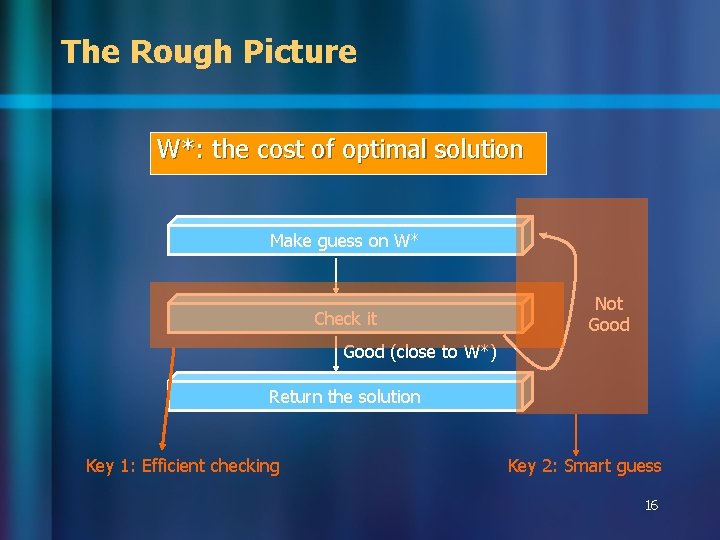
The Rough Picture W*: the cost of optimal solution Make guess on W* Check it Not Good (close to W*) Return the solution Key 1: Efficient checking Key 2: Smart guess 16

Key 1: Efficient Checking Benefit of guess • Only maintain the solutions with cost no greater than the guessed cost • Accelerate DP 17

The Oracle n Oracle (x): Setup the checker, able to decide whether x>W* or not upper and lower bounds of cost W* – Without knowing W* – Answer efficiently Guess x within the bounds Oracle (x) Update the bounds 18

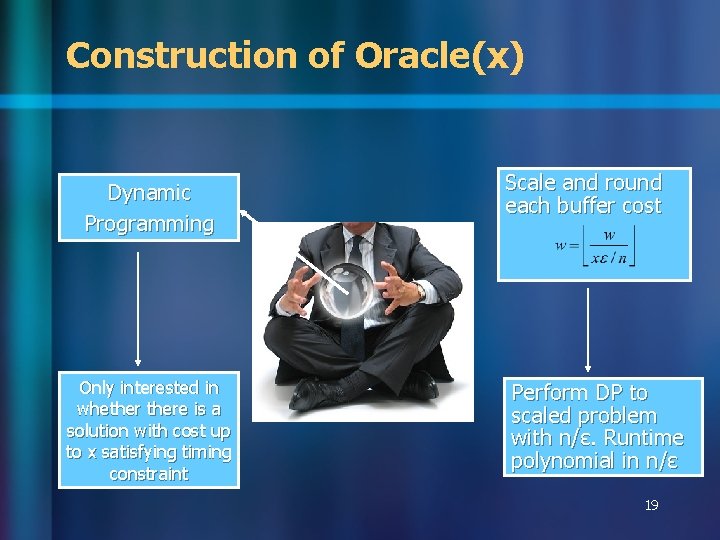
Construction of Oracle(x) Dynamic Programming Only interested in whethere is a solution with cost up to x satisfying timing constraint Scale and round each buffer cost Perform DP to scaled problem with n/ɛ. Runtime polynomial in n/ɛ 19

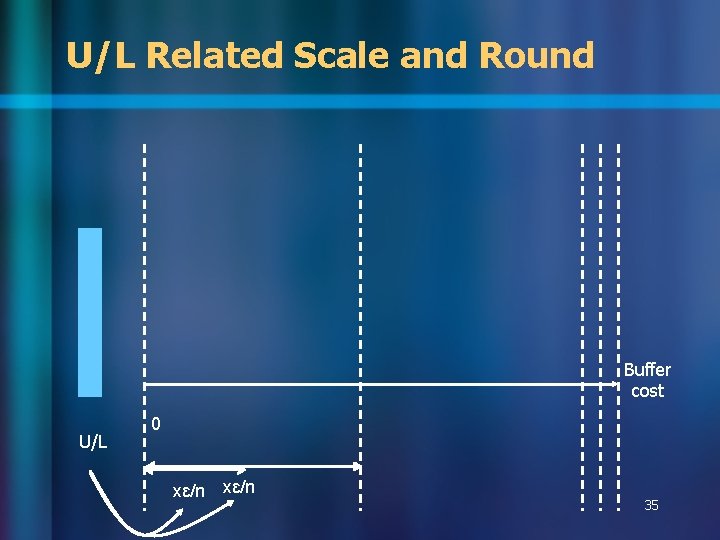
Scaling and Rounding 0 Rounding error at each buffer xɛ/n, total rounding error xɛ. buffer costs are integers • Larger x: larger error, fewer due tocosts rounding and are distinct and faster bounded by n/ɛ. • Smaller x: smaller error, more distinct costs and slower • Rounding is the reason of acceleration xɛ/n 2 xɛ/n 3 xɛ/n Buffer cost 4 xɛ/n 20

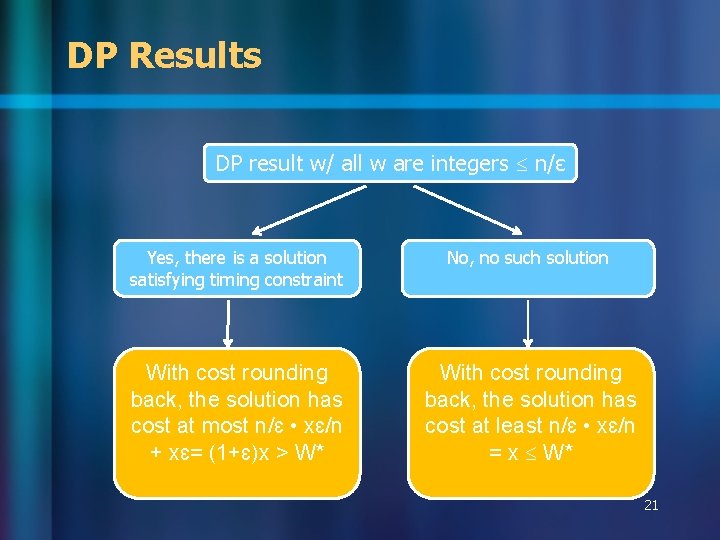
DP Results DP result w/ all w are integers n/ɛ Yes, there is a solution satisfying timing constraint No, no such solution With cost rounding back, the solution has cost at most n/ɛ • xɛ/n + xɛ= (1+ɛ)x > W* With cost rounding back, the solution has cost at least n/ɛ • xɛ/n = x W* 21

Rounding on Q n # solutions bounded by # distinct W and Q # W = O(n/ɛ 1) n #Q n # non-dominated solutions is O(mn/ɛ 1ɛ 2) n – Rounding before DP – Round up Q to nearest value in {0, ɛ 2 T/m , 2ɛ 2 T/m, 3ɛ 2 T/m, …, T }, in branch merge (m is # sinks) – Rounding during DP – # Q = O(m/ɛ 2) 0 ɛ 2 T/m 2ɛ 2 T/m 3ɛ 2 T/m 4ɛ 2 T/m 22

Q-W Rounding Before Branch Merge Q T 4ɛ 2 T/m 3ɛ 2 T/m 2ɛ 2 T/m 0 1 2 3 4 n/ɛ 1 W

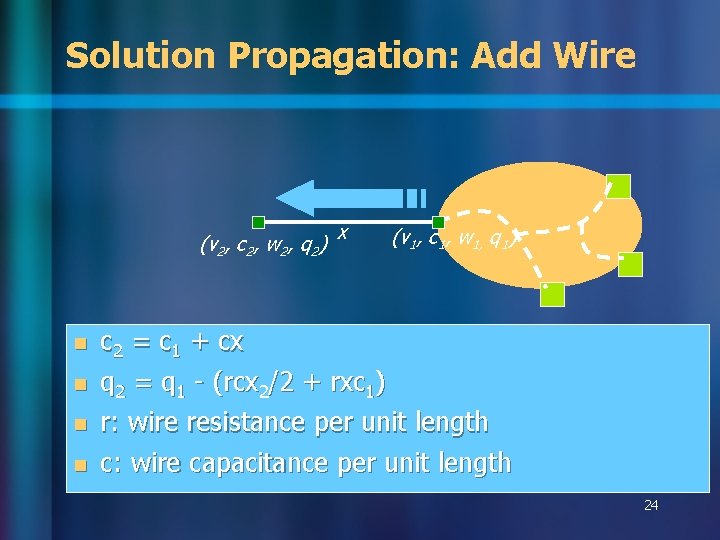
Solution Propagation: Add Wire (v 2, c 2, w 2, q 2) x (v 1, c 1, w 1, q 1) n c 2 = c 1 + cx q 2 = q 1 - (rcx 2/2 + rxc 1) r: wire resistance per unit length n c: wire capacitance per unit length n n 24

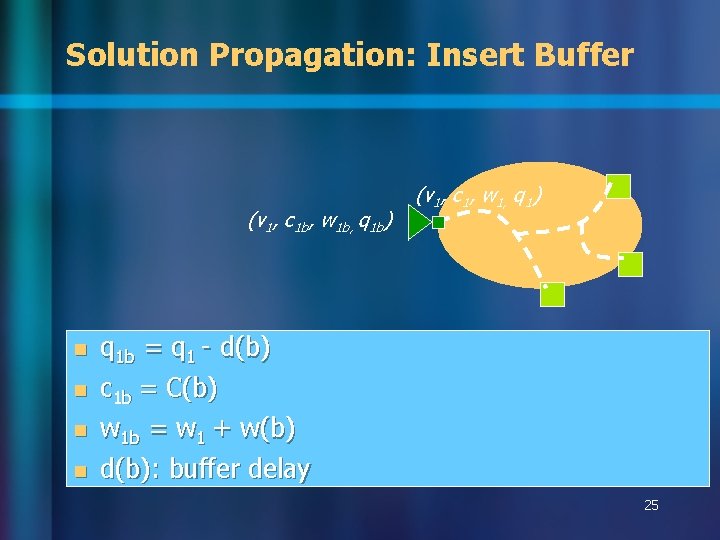
Solution Propagation: Insert Buffer (v 1, c 1 b, w 1 b, q 1 b) n q 1 b = q 1 - d(b) c 1 b = C(b) w 1 b = w 1 + w(b) n d(b): buffer delay n n (v 1, c 1, w 1, q 1) 25

Buffer Insertion Runtime

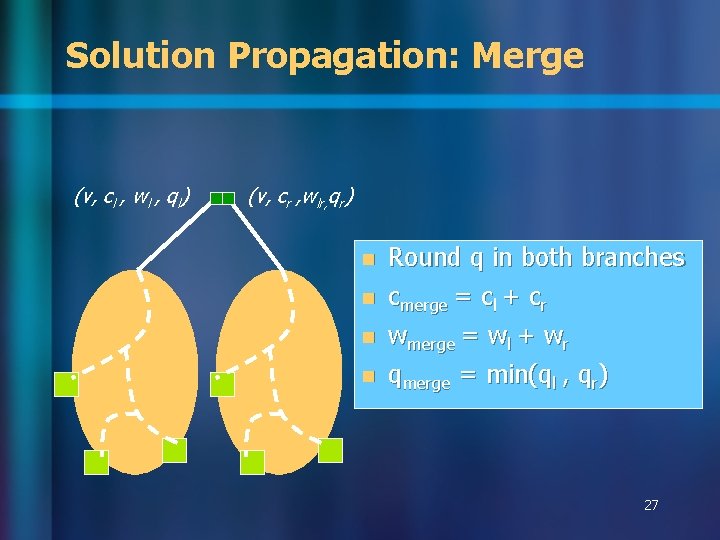
Solution Propagation: Merge (v, cl , wl , ql) (v, cr , wlr, qr) n n Round q in both branches cmerge = cl + cr wmerge = wl + wr qmerge = min(ql , qr) 27

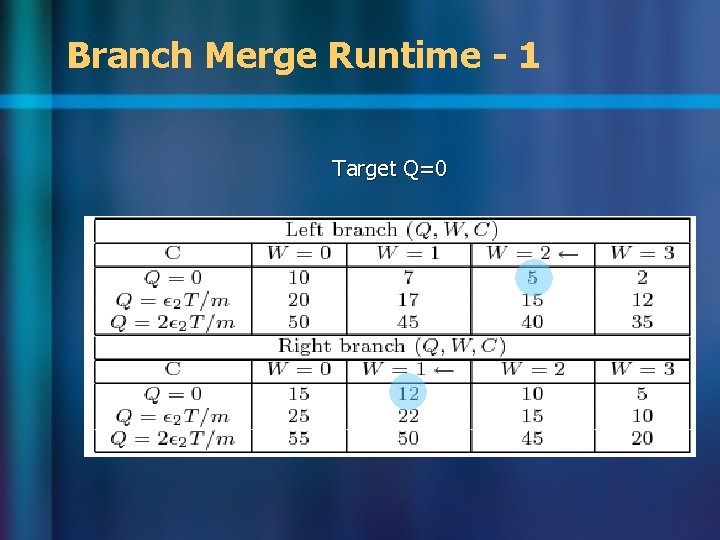
Branch Merge Runtime - 1 Target Q=0

Branch Merge Runtime - 2 Target Q= ɛ 2 T/m

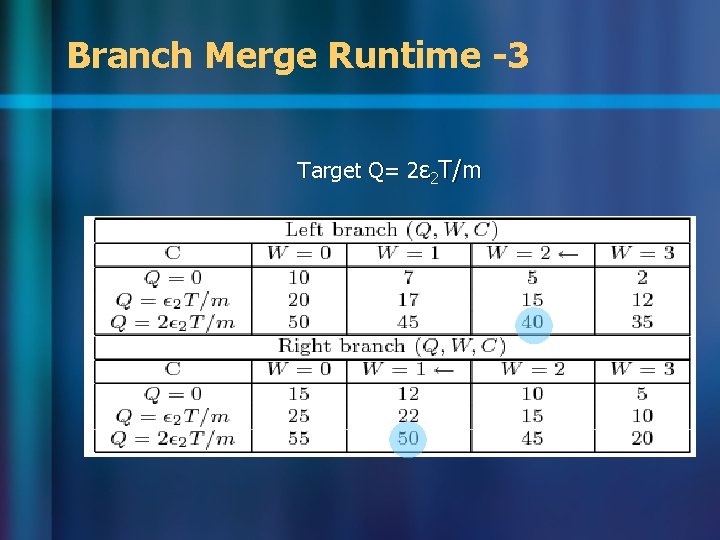
Branch Merge Runtime -3 Target Q= 2ɛ 2 T/m

Branch Merge Runtime -4

Timing-Cost Approximate DP n Lemma: a buffering solution with cost at most (1+ɛ 1)W* and with timing at most (1+ɛ 2)T can be computed in time 32

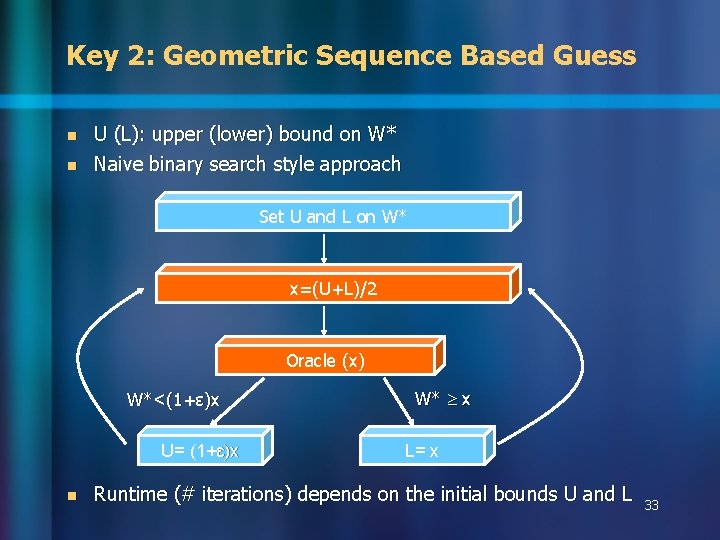
Key 2: Geometric Sequence Based Guess n n U (L): upper (lower) bound on W* Naive binary search style approach Set U and L on W* x=(U+L)/2 Oracle (x) W*<(1+ɛ)x U= (1+ɛ)x n W* x L= x Runtime (# iterations) depends on the initial bounds U and L 33

Adapt ɛ 1 n Rounding factor xɛ 1/n for W n Larger ɛ 1: faster with rough estimation Smaller ɛ 1: slower with accurate estimation Adapt ɛ 1 according to U and L n n 34

U/L Related Scale and Round Buffer cost U/L 0 xɛ/n 35

Conceptually n n Begin with large ɛ 1 and progressively reduce it (towards ɛ) according to U/L as x approaches W* Fix ɛ 2=ɛ in rounding Q for limiting timing violation • Set ɛ 1 as a geometric sequence of …, 8, 4, 2, 1, 1/2, …, ɛ • One run of DP takes about O(n/ɛ 1) time. Total runtime is bounded by the last run as O(… + n/8 + n/4 + n/2 + … + n/ɛ) = O(n/ɛ), independent of # iterations 36

Oracle Query Till U/L<2 37

Mathematically 38

The Algorithmic Flow Set U and L of W* Adapting ɛ 1 =[U/L-1]1/2 Update U or L Set x=[UL/(1+ ɛ 1)]1/2 Oracle (x) U/L<2 Compute final solution 39

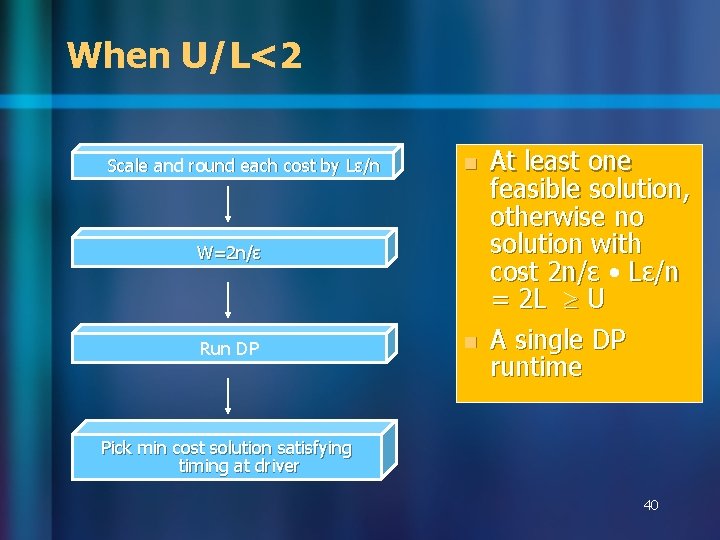
When U/L<2 Scale and round each cost by Lɛ/n n W=2 n/ɛ Run DP n At least one feasible solution, otherwise no solution with cost 2 n/ɛ • Lɛ/n = 2 L U A single DP runtime Pick min cost solution satisfying timing at driver 40

Main Theorem § Theorem: a (1+ ɛ) approximation to the timing constrained minimum cost buffering problem can be computed in O(m 2 n 2 b/ɛ 3+ n 3 b 2/ɛ) time for 0<ɛ<1 and in O(m 2 n 2 b/ɛ+mn 2 b+n 3 b) time for ɛ 1

Experiments n Experimental Setup – 1000 industrial nets – 48 buffer types including non-inverting buffers and inverting buffers n Compared to Dynamic Programming 42

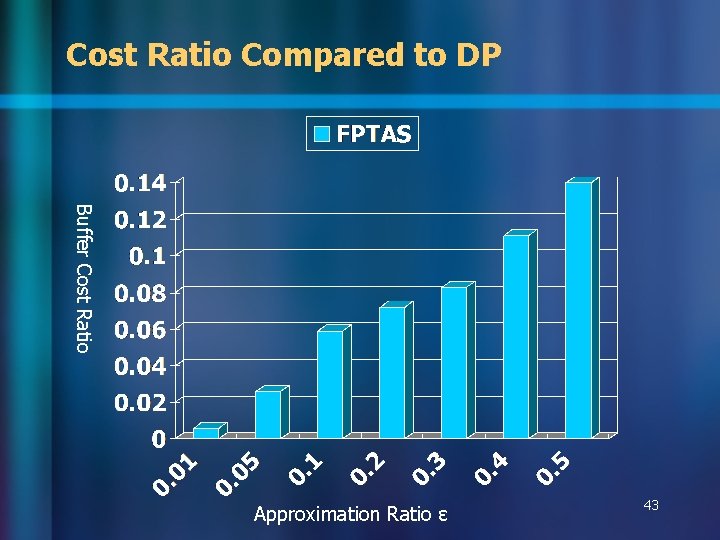
Cost Ratio Compared to DP Buffer Cost Ratio Approximation Ratio ɛ 43

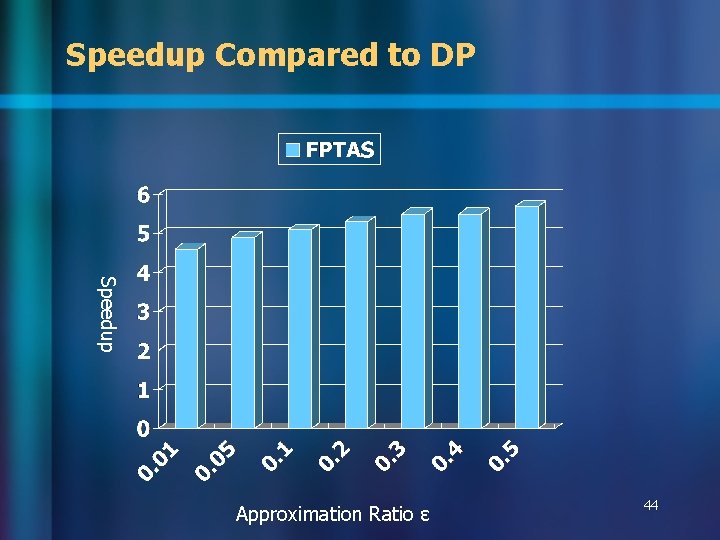
Speedup Compared to DP Speedup Approximation Ratio ɛ 44

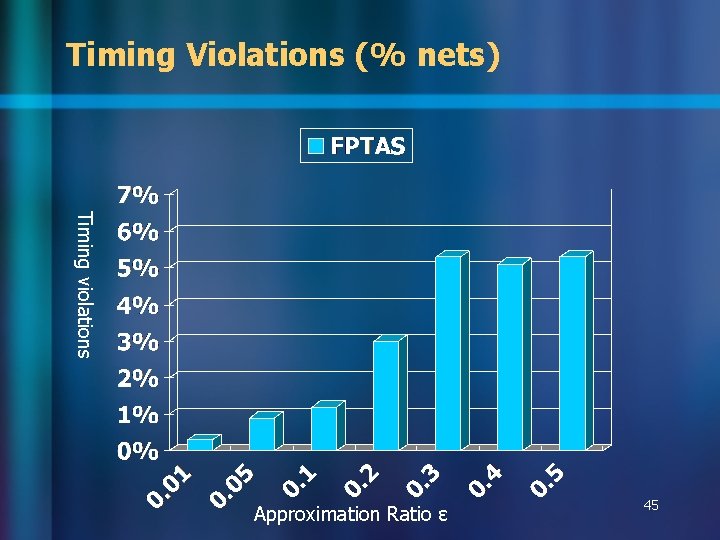
Timing Violations (% nets) Timing violations Approximation Ratio ɛ 45

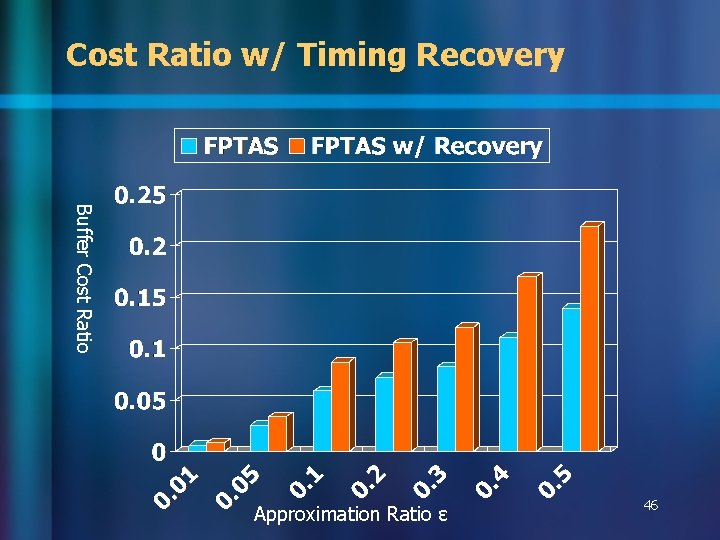
Cost Ratio w/ Timing Recovery Buffer Cost Ratio Approximation Ratio ɛ 46

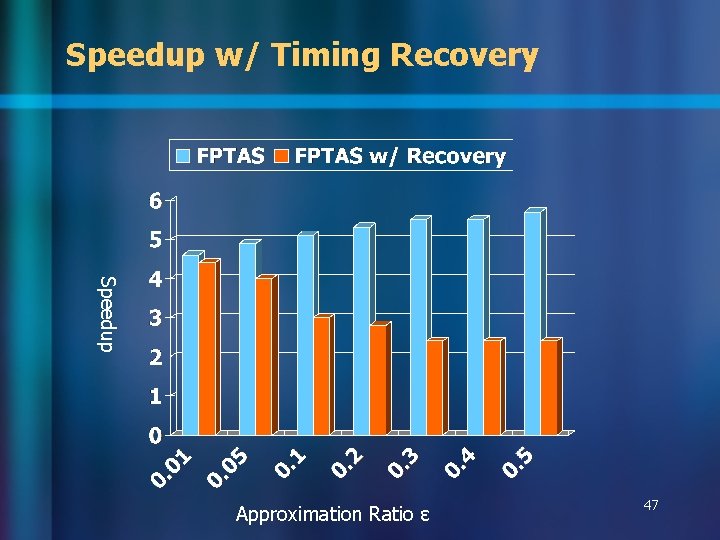
Speedup w/ Timing Recovery Speedup Approximation Ratio ɛ 47

Observations n Without timing recovery – – – n FPTAS always achieves theoretical guarantee Larger ɛ leads to more speedup On average about 5 x faster than dynamic programming Can run 4. 6 x faster with 0. 57% solution degradation <5% nets with timing violations With timing recovery – FPTAS well approximates the optimal solutions – Can still have >4 x speedup 48

Our Bridge NP-Hardness Complexity Exponential Time Algorithm

Conclusion n n Propose a (1+ ɛ) approximation for timing constrained minimum cost buffering for any ɛ > 0 – Runs in O(m 2 n 2 b/ɛ 3+ n 3 b 2/ɛ) time – Timing-cost approximate dynamic programming – Double-ɛ geometric sequence based oracle search – 5 x speedup in experiments – Few percent additional buffers as guaranteed theoretically The first provably good approximation algorithm on this problem 50

Thanks 51