A Formal Model of Modularity in AspectOriented Programming

A Formal Model of Modularity in Aspect-Oriented Programming Jonathan Aldrich 15 -819: Objects and Aspects Carnegie Mellon University

Outline AOP Modularity Challenges n Open Modules n A Bit of Formality n Comparison to Aspect-Aware Interfaces n Lessons Learned and Discussion n

Modularity and Encapsulation n Parnas’ advice: n n Encapsulation n Modularize a system to hide information that may change A mechanism for enforcing information hiding Java classes & packages, ML modules… Aspect-oriented Programming n More flexible ways of modularizing a system

Is AOP Modular? Back to Parnas: Does AOP hide information that is likely to change? n Yes, within the aspect n n n Aspect code can be evolved separately No, not within the base code n Minor changes to base code break the aspect

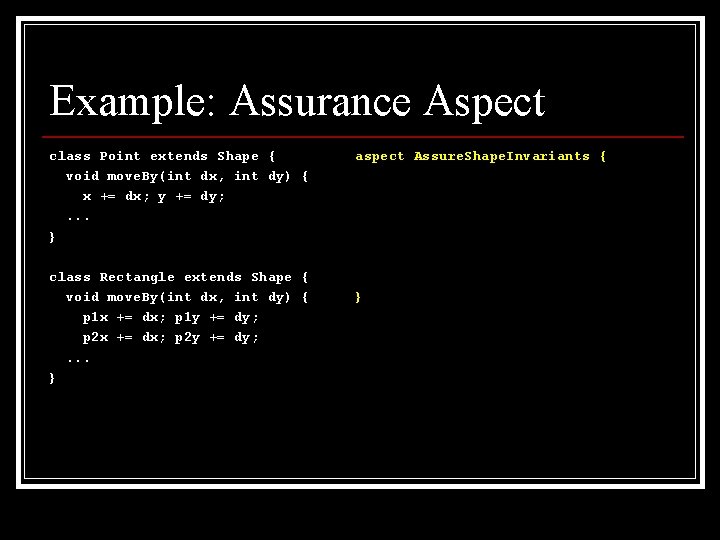
Example: Assurance Aspect class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . }

Example: Assurance Aspect class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1 x += dx; p 1 y += dy; p 2 x += dx; p 2 y += dy; . . . }

Example: Assurance Aspect class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1 x += dx; p 1 y += dy; p 2 x += dx; p 2 y += dy; . . . } aspect Assure. Shape. Invariants { }

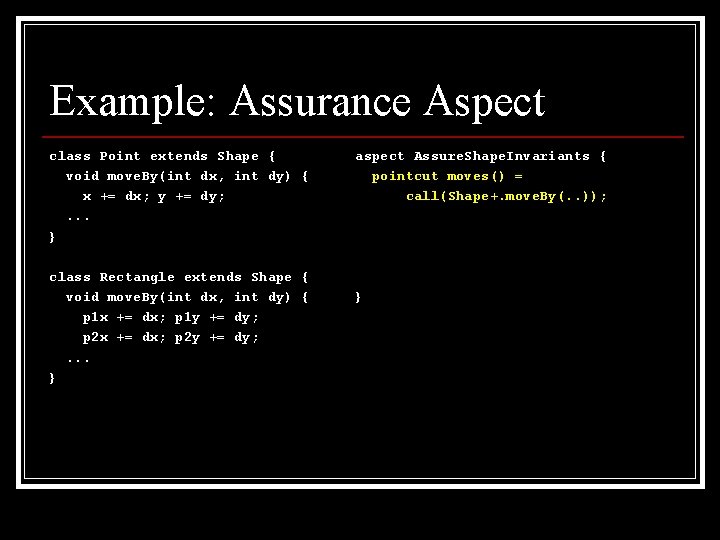
Example: Assurance Aspect class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1 x += dx; p 1 y += dy; p 2 x += dx; p 2 y += dy; . . . } aspect Assure. Shape. Invariants { pointcut moves() = call(Shape+. move. By(. . )); }

Example: Assurance Aspect class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1 x += dx; p 1 y += dy; p 2 x += dx; p 2 y += dy; . . . } aspect Assure. Shape. Invariants { pointcut moves() = call(Shape+. move. By(. . )); after(): moves() { scene. check. Invariants(); } }

Example: Broken Assurance Aspect class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1 x += dx; p 1 y += dy; p 2 x += dx; p 2 y += dy; . . . } Change representation to use Point aspect Assure. Shape. Invariants { pointcut moves() = call(Shape+. move. By(. . )); after(): moves() { scene. check. Invariants(); } }

Example: Broken Assurance Aspect class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1. move. By(dx, dy); p 2. move. By(dx, dy); . . . } Change representation to use Point aspect Assure. Shape. Invariants { pointcut moves() = call(Shape+. move. By(. . )); after(): moves() { scene. check. Invariants(); } }

Example: Broken Assurance Aspect class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1. move. By(dx, dy); p 2. move. By(dx, dy); . . . } Change representation to use Point aspect Assure. Shape. Invariants { pointcut moves() = call(Shape+. move. By(. . )); after(): moves() { scene. check. Invariants(); } } Now the scene invariants are checked in the middle of a Rectangle move—when they might be broken!

Analysis n Aspects can violate information hiding n n Similar to OO Fragile Base Class Problem n n Assurance aspect depends on Shape internals Observing impl. dependant calling patterns Can fix each individual problem n Better: use modules to forestall issue

Fix #1: external advice class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1 x += dx; p 1 y += dy; p 2 x += dx; p 2 y += dy; . . . } aspect Assure. Shape. Invariants { pointcut moves(): call(Shape+. move. By(. . )) && !within(shape. *); after(): moves() { scene. check. Invariants(); } } Only specifies calls that are external to the shape package

Fix #2: semantic pointcut class Point extends Shape { void move. By(int dx, int dy) { x += dx; y += dy; . . . } class Rectangle extends Shape { void move. By(int dx, int dy) { p 1 x += dx; p 1 y += dy; p 2 x += dx; p 2 y += dy; . . . } class Shape { public pointcut moves(): call(Shape+. move. By(. . )); } aspect Assure. Shape. Invariants { after(): Shape. moves() { scene. check. Invariants(); } } Move pointcut to the shape package Now the shape maintainer is responsible for preserving its semantics when shapes evolve

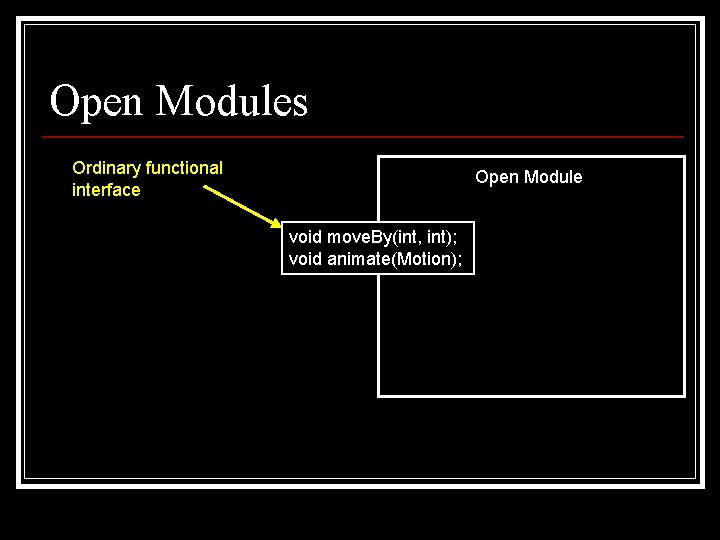
Open Modules Ordinary functional interface Open Module void move. By(int, int); void animate(Motion);

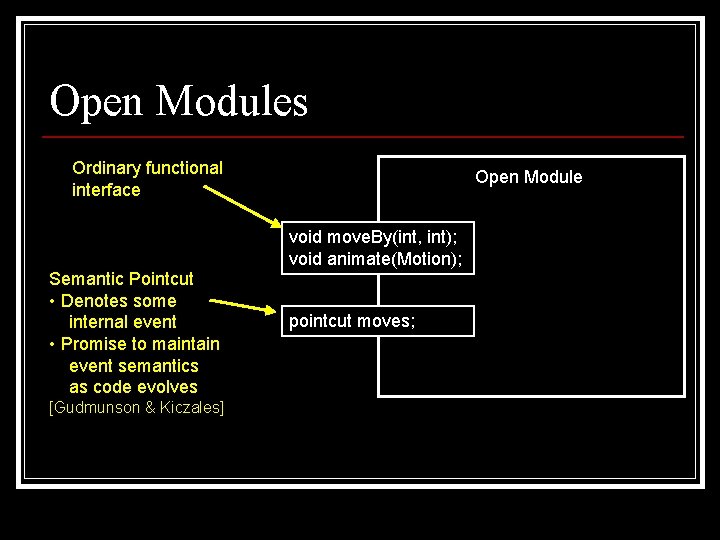
Open Modules Ordinary functional interface Open Module void move. By(int, int); void animate(Motion); Semantic Pointcut • Denotes some internal event • Promise to maintain event semantics as code evolves [Gudmunson & Kiczales] pointcut moves;

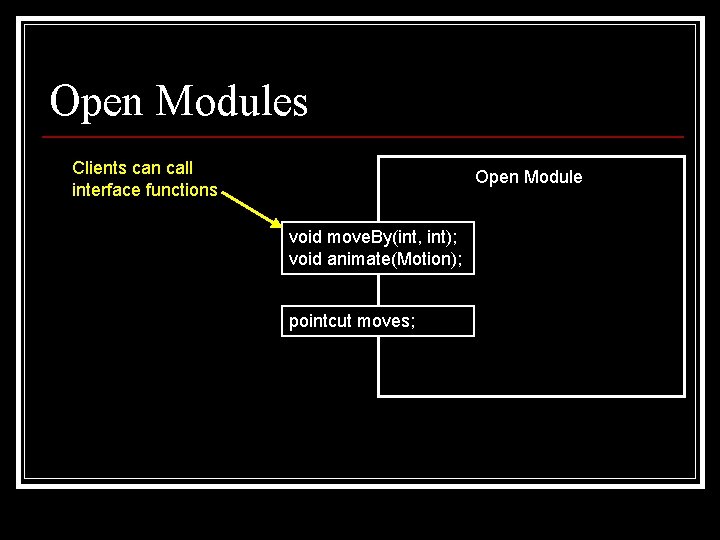
Open Modules Clients can call interface functions Open Module void move. By(int, int); void animate(Motion); pointcut moves;

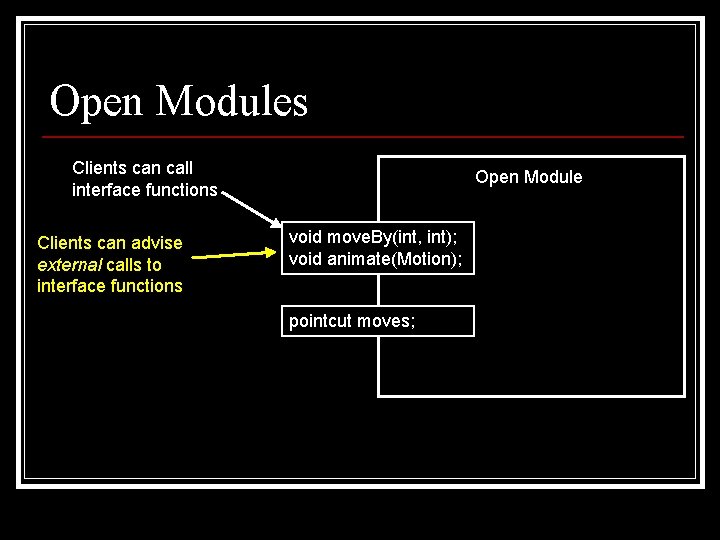
Open Modules Clients can call interface functions Clients can advise external calls to interface functions Open Module void move. By(int, int); void animate(Motion); pointcut moves;

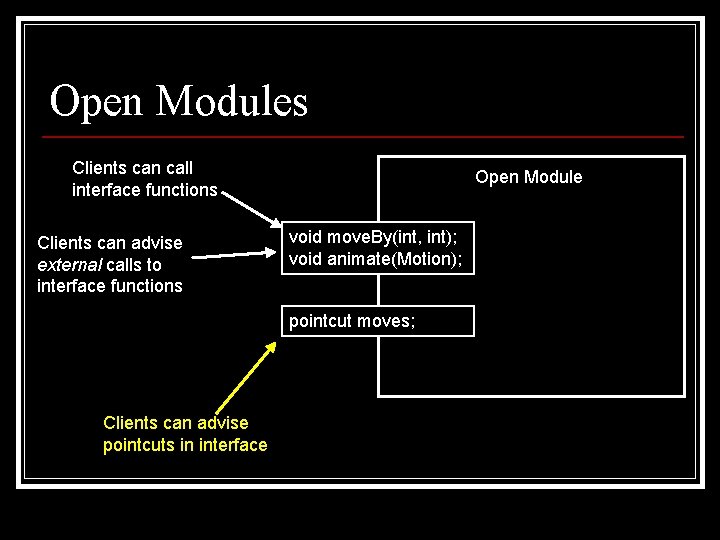
Open Modules Clients can call interface functions Clients can advise external calls to interface functions Open Module void move. By(int, int); void animate(Motion); pointcut moves; Clients can advise pointcuts in interface

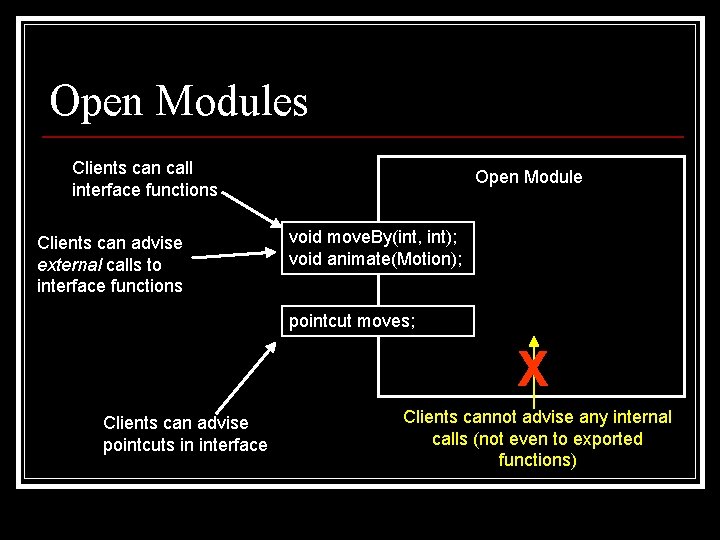
Open Modules Clients can call interface functions Clients can advise external calls to interface functions Open Module void move. By(int, int); void animate(Motion); pointcut moves; X Clients can advise pointcuts in interface Clients cannot advise any internal calls (not even to exported functions)

Open Module Properties: Equivalence n Motivation n Rules describe when changes could affect clients Can be used to prove correctness of refactorings Bisimulation-based equivalence n n All functions map args to same results Invoke internal pointcuts in same way n Same sequence, same context

Open Module Properties: Abstraction n Verifies correctness of equivalence rules n n Shows that information hiding works Informal statement of theorem n n Consider two module implementations that are equivalent according to the bisimulation rules No client code can distinguish the behavior of these modules (even by using aspects) n Note: this would fail for Aspect. J!

Comparison to Aspect-Aware Interfaces n AAI: more obliviousness, extensibility n n OM: truly separate development n n Don’t have to anticipate semantic pointcuts AAI cannot be computed in this case OM: shows technical properties of AAI n n n AAI is an OM interface computed by tools Abstraction supports evolvability Not all information in AAI is needed n n Don’t need exact advice Don’t need pointcuts for external calls to interface functions

Tool and Language Implications n Tools: Provide editable interface pointcuts n n Tools: Support dependency tracking n n n Change base code and affected pointcuts at the same time Let you know when you’re depending on impl. Warn you to re-check pointcuts when impl. Changes Language n Make it easier to write non-invasive pointcuts

Discussion Extensibility vs. Reasoning n Tool vs. Language-based reasoning n Open Modules into real AOP systems n Analysis based on Open Modules n

End of Presentation/Extra Slides

Tiny. Aspect Example (* fibonacci function *) val fib = fn x: int => 1 around call(fib) (x: int) = if (x > 2) then fib(x-1) + fib(x-2) else proceed x (* caching library *) val in. Cache = fn. . . val lookup. Cache = fn. . . val update. Cache = fn. . . (* advice to cache calls to fib *) pointcut cache. Function = call(fib) around cache. Function(x: int) = if (in. Cache x) then lookup. Cache x else let v = proceed x in update. Cache x v; v

Tiny. Aspect: Syntax

Evaluation n Environment captures advice n Declarations add labels to environment n Functions are looked up just before application

Evaluation n Environment captures advice n Declarations add labels to environment n Advice updates environment

Tiny. Aspect: Values and Contexts

Tiny. Aspect: Reduction Rules

Tiny. Aspect: Expression Typing

Tiny. Aspect: Declaration Typing

Tiny. Aspect: Properties

Open Modules: Syntax

Open Modules: Example structure Math = struct val fib = fn x: int => 1 around call(fib) (x: int) = … structure cache. Fib = Cache(struct pointcut f = call(fib) end : > sig fib : int->int end structure Cache = functor(X : sig f : pc(int->int) end) => struct around X. f(x: int) =. . . (* same definition *) end

Open Modules: Semantics n Standard type system n n Signature subtyping permitted Runtime semantics mostly standard n E. g, functor application uses substitution

Open Modules: Semantics n Sealing has operational effect n Value bindings given fresh labels n n n External advice doesn’t affect internal calls C. f. “freeze” operator in Jigsaw, other systems Pointcuts are unchanged

Reynolds’ Abstraction Property n No client can distinguish two modules that are “observationally equivalent” (c. f. Pi-calculus) n n calling functions in interface advising external calls to interface advising pointcuts in interface Means that information hiding works n You can change the internals of a module w/o affecting clients

Observational Equivalence n Functions behave equivalently for all args n Expression evaluation must be bisimilar n w. r. t. a set of available labels Can take any step other than looking up n Can both look up the same label in n

Formal Abstraction Theorem n Proof insight n n n Client can only advise labels in Libraries treat these labels equivalently Key invariant n Clients are structurally identical n Except for embedded equivalent values