A FIZIKAI SSZEFGGSEK SZRMAZTATSNAK ALAPJAI dr Majr Jnos

A FIZIKAI ÖSSZEFÜGGÉSEK SZÁRMAZTATÁSÁNAK ALAPJAI dr. Majár János

CÉLOK, MEGJEGYZÉSEK - A fizikai összefüggések helyes felírásához szükséges tudások átadása - Minta-gyakorlatok kidolgozása, melyek segítségével ezek használata fejleszthető - Ezek segítségével a feladatmegoldás során a részeredmények és a formális végeredmény is ellenőrizhető (ellenőrizendő) - Az érintett területek rövid, összefoglaló bemutatása - Az egyes diák elkészítésénél igyekeztem csak olyan funkciókat használni, amelyek csak az alapprogramra építenek.

TARTALOM - Vektorok, azok felírása derékszögű Descartes-koordinátarendszerben - Vektorokkal végzett műveletek (koordinátarendszerben is) - Vektorok és skalárok között végzett helyes műveletek kiválasztása - Mértékegységek, azok helyes használata a számolások során - Prefixumok, mértékegységek átváltása - Példaként alapvető fizikai mennyiségek, azok mértékegységei, meghatározásuk a Mechanika területéről - Gyakorlatok – ezek tényleg csak mintául szolgálnak, ezek alapján hasonlóak könnyedén kidolgozhatóak, a mennyiségek felírása után más tudományterület esetében is.

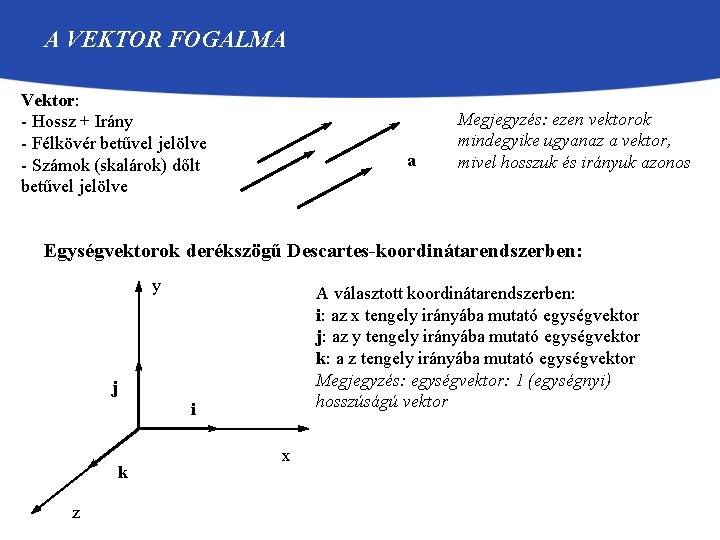
A VEKTOR FOGALMA Vektor: - Hossz + Irány - Félkövér betűvel jelölve - Számok (skalárok) dőlt betűvel jelölve a Megjegyzés: ezen vektorok mindegyike ugyanaz a vektor, mivel hosszuk és irányuk azonos Egységvektorok derékszögű Descartes-koordinátarendszerben: y A választott koordinátarendszerben: i: az x tengely irányába mutató egységvektor j: az y tengely irányába mutató egységvektor k: a z tengely irányába mutató egységvektor Megjegyzés: egységvektor: 1 (egységnyi) hosszúságú vektor j i k z x

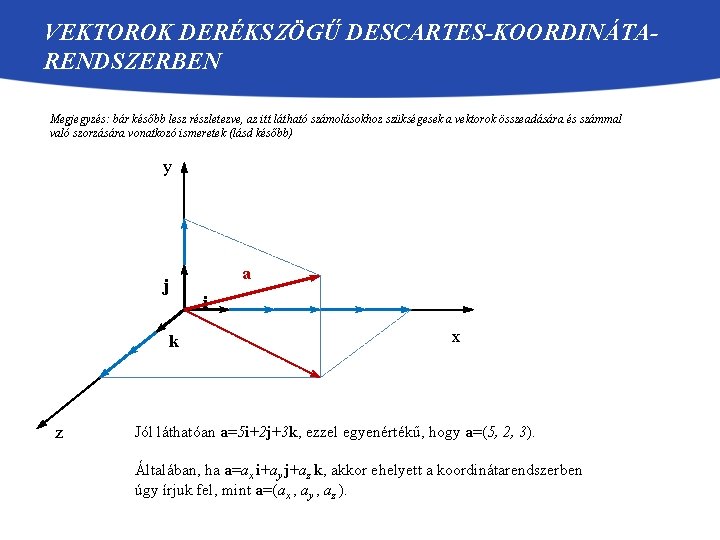
VEKTOROK DERÉKSZÖGŰ DESCARTES-KOORDINÁTARENDSZERBEN Megjegyzés: bár később lesz részletezve, az itt látható számolásokhoz szükségesek a vektorok összeadására és számmal való szorzására vonatkozó ismeretek (lásd később) y j k z a i x Jól láthatóan a=5 i+2 j+3 k, ezzel egyenértékű, hogy a=(5, 2, 3). Általában, ha a=ax i+ay j+az k, akkor ehelyett a koordinátarendszerben úgy írjuk fel, mint a=(ax , ay , az ).

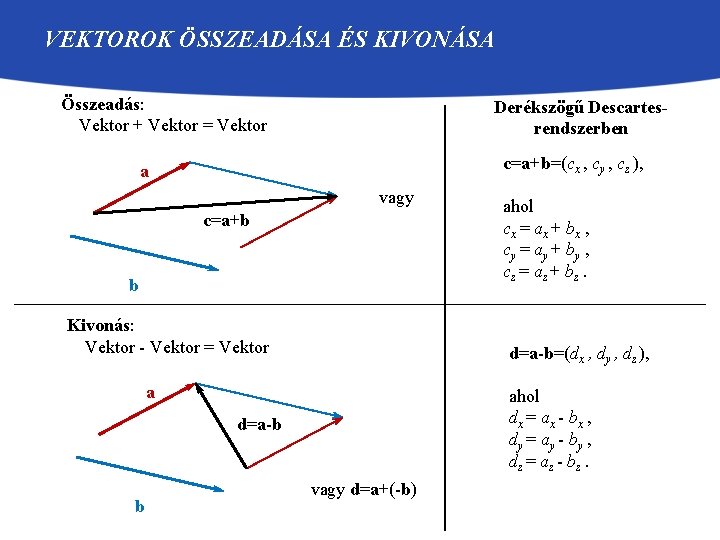
VEKTOROK ÖSSZEADÁSA ÉS KIVONÁSA Összeadás: Vektor + Vektor = Vektor Derékszögű Descartesrendszerben c=a+b=(cx , cy , cz ), a vagy c=a+b b Kivonás: Vektor - Vektor = Vektor d=a-b=(dx , dy , dz ), a ahol dx = ax - bx , dy = ay - by , dz = az - bz. d=a-b b ahol cx = ax + bx , cy = ay + by , cz = az + bz. vagy d=a+(-b)

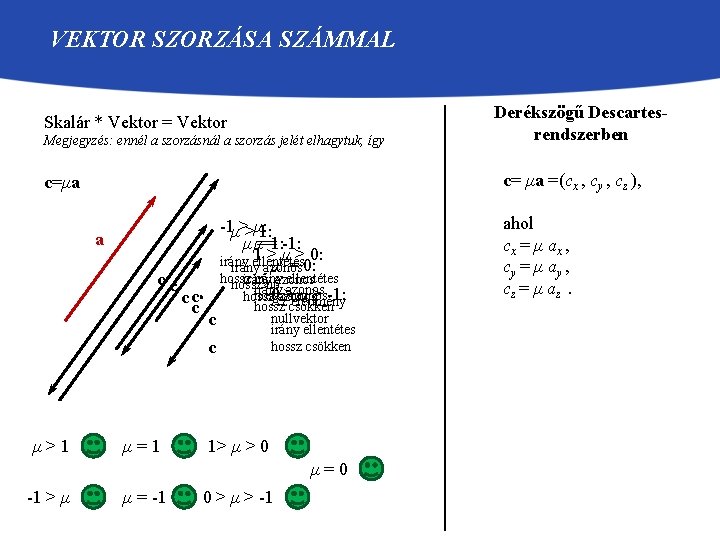
VEKTOR SZORZÁSA SZÁMMAL Skalár * Vektor = Vektor Megjegyzés: ennél a szorzásnál a szorzás jelét elhagytuk, így c= μa =(cx , cy , cz ), c=μa -1μ>>μ: 1: μ μ= =1: -1: 1 > μ > 0: irány ellentétes μ = 0: irány azonos a cc μ>1 μ=1 cc c hossz nőnőazonos irány ellentétes irány hossz irány 0 Az >azonos μ > -1: hossz azonos eredmény hossz csökken nullvektor c irány ellentétes hossz csökken c 1> μ > 0 μ=0 -1 > μ Derékszögű Descartesrendszerben μ = -1 0 > μ > -1 ahol cx = μ ax , cy = μ ay , cz = μ az.

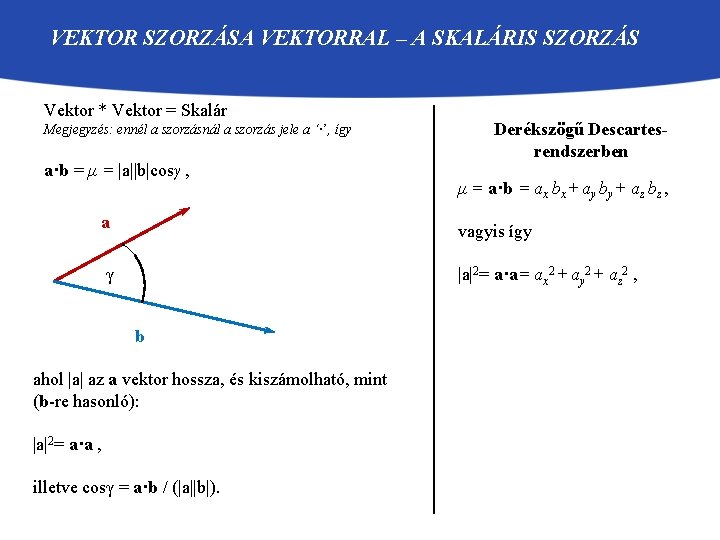
VEKTOR SZORZÁSA VEKTORRAL – A SKALÁRIS SZORZÁS Vektor * Vektor = Skalár Megjegyzés: ennél a szorzásnál a szorzás jele a ‘·’, így a·b = μ = |a||b|cosγ , a Derékszögű Descartesrendszerben μ = a·b = ax bx + ay by + az bz , vagyis így γ |a|2= a·a= ax 2 + ay 2 + az 2 , b ahol |a| az a vektor hossza, és kiszámolható, mint (b-re hasonló): |a|2= a·a , illetve cosγ = a·b / (|a||b|).

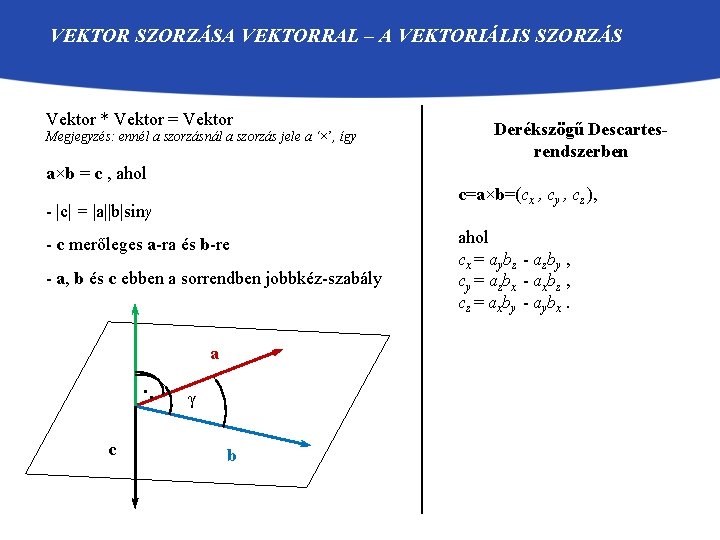
VEKTOR SZORZÁSA VEKTORRAL – A VEKTORIÁLIS SZORZÁS Vektor * Vektor = Vektor Megjegyzés: ennél a szorzásnál a szorzás jele a ‘×’, így Derékszögű Descartesrendszerben a×b = c , ahol c=a×b=(cx , cy , cz ), - |c| = |a||b|sinγ - c merőleges a-ra és b-re - a, b és c ebben a sorrendben jobbkéz-szabály a ·· c γ b ahol cx = aybz - azby , cy = azbx - axbz , cz = axby - aybx.

MEGJEGYZÉSEK Skaláris szorzás szélsőhelyzetei 1. a azonos irányú b-vel: γ = 0 -> a·b = μ = |a||b| 2. a merőleges b-re: γ = 90° -> a·b = μ = 0 3. a ellentétes irányú b-vel: γ = 180° -> a·b = μ = - |a||b| Vektoriális szorzás szélsőhelyzetei 1. a párhuzamos b-vel: γ = 0 -> |c| = 0, c nullvektor 2. a merőleges b-re: γ = 90° -> |c| = |a||b| Vektoriális szorzás fordított sorrendben Mivel a, b és c ebben a sorrendben jobbkéz-szabály szerint kell működjön, ha megfordítjuk a sorrendet: a×b = - b×a. Derékszögű Descartesrendszerben Ha a skaláris szorzat értéke 0, a két vektor merőleges (egyik sem nullvektor). -> Egyszerű feltétel, ha koordinátákkal számolunk. Ha a vektoriális szorzat vektor mindegyik komponense 0, a két vektor párhuzamos (egyik sem nullvektor). -> Egyszerű feltétel, ha koordinátákkal számolunk. Ha a vektoriális szorzatot komponensenként felírjuk, ez a szabály jól láthatóan teljesül a két vektor szerepének felcserélésekor.

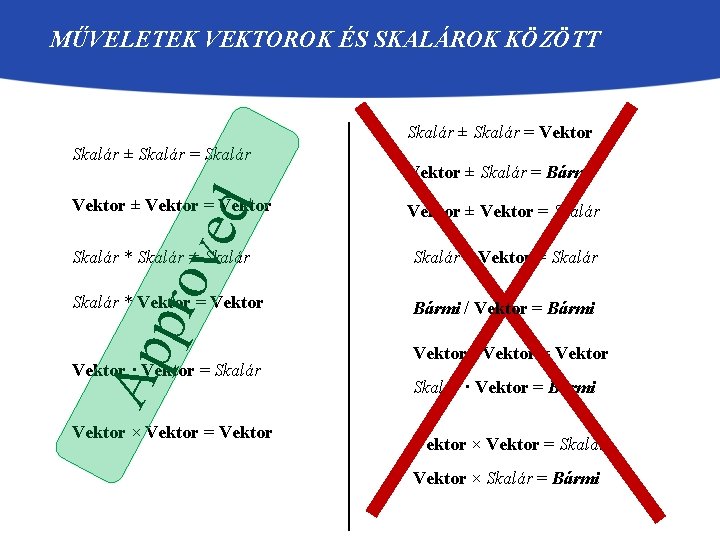
MŰVELETEK VEKTOROK ÉS SKALÁROK KÖZÖTT Skalár ± Skalár = Vektor Skalár ± Skalár = Skalár ove d Vektor ± Vektor = Vektor ± Skalár = Bármi Vektor ± Vektor = Skalár * Vektor = Vektor Bármi / Vektor = Bármi Ap pr Skalár * Skalár = Skalár Vektor · Vektor = Skalár Vektor × Vektor = Vektor · Vektor = Vektor Skalár · Vektor = Bármi Vektor × Vektor = Skalár Vektor × Skalár = Bármi

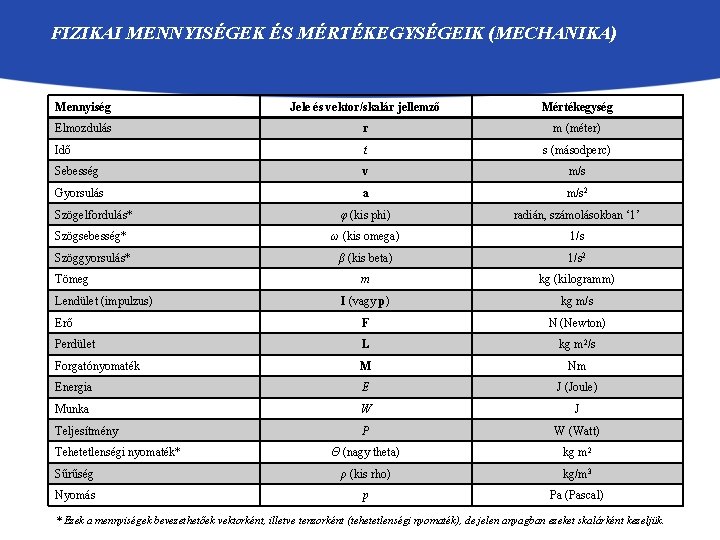
FIZIKAI MENNYISÉGEK ÉS MÉRTÉKEGYSÉGEIK (MECHANIKA) Mennyiség Jele és vektor/skalár jellemző Mértékegység Elmozdulás r m (méter) Idő t s (másodperc) Sebesség v m/s Gyorsulás a m/s 2 Szögelfordulás* φ (kis phi) radián, számolásokban ‘ 1’ Szögsebesség* ω (kis omega) 1/s Szöggyorsulás* β (kis beta) 1/s 2 m kg (kilogramm) I (vagy p) kg m/s Erő F N (Newton) Perdület L kg m 2/s Forgatónyomaték M Nm Energia E J (Joule) Munka W J Teljesítmény P W (Watt) Θ (nagy theta) kg m 2 Sűrűség ρ (kis rho) kg/m 3 Nyomás p Pa (Pascal) Tömeg Lendület (impulzus) Tehetetlenségi nyomaték* * Ezek a mennyiségek bevezethetőek vektorként, illetve tenzorként (tehetetlenségi nyomaték), de jelen anyagban ezeket skalárként kezeljük.

MÉRTÉKEGYSÉGEK HELYES KEZELÉSE - A mértékegységek szorzás során összeszorzódnak - A mértékegységek osztás során ugyanúgy osztandóak egymással, mint a mennyiségek - Differenciálás során a derivált mennyiség mértékegységét osztjuk a változó mértékegységével - Integrálás során az integrált mennyiség mértékegységét szorozzuk a változó mértékegységével - Csak azonos mértékegységű mennyiségek adhatóak össze, vagy vonhatóak ki egymásból! - Egy egyenlet két oldalán azonos mértékegységű mennyiségek állhatnak! - Egy-egy mennyiség mértékegysége kikövetkeztethető a meghatározásából. - Egy adott fizikai mennyiség mértékegysége jelölhető úgy is, hogy a mennyiség jelét [ ] rázójelek közé írjuk, például a sebesség mértékegysége m/s, vagy [v].

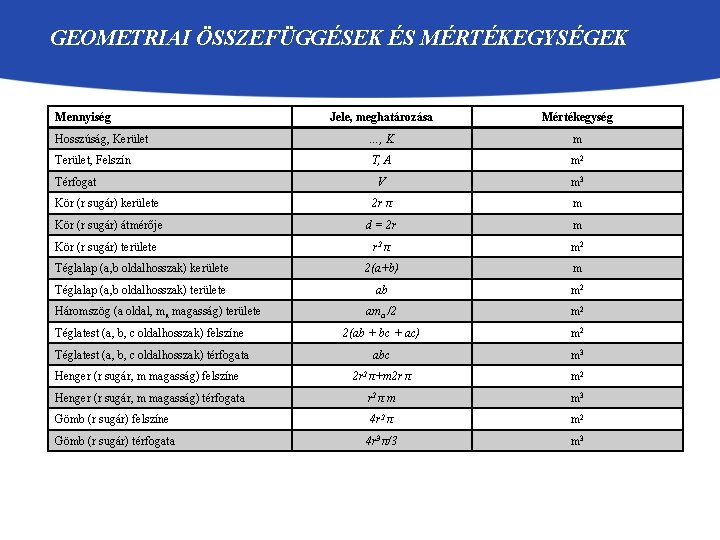
GEOMETRIAI ÖSSZEFÜGGÉSEK ÉS MÉRTÉKEGYSÉGEK Mennyiség Jele, meghatározása Mértékegység Hosszúság, Kerület …, K m Terület, Felszín T, A m 2 V m 3 Kör (r sugár) kerülete 2 r π m Kör (r sugár) átmérője d = 2 r m Kör (r sugár) területe r 2 π m 2 Téglalap (a, b oldalhosszak) kerülete 2(a+b) m Téglalap (a, b oldalhosszak) területe ab m 2 ama /2 m 2 Téglatest (a, b, c oldalhosszak) felszíne 2(ab + bc + ac) m 2 Téglatest (a, b, c oldalhosszak) térfogata abc m 3 Henger (r sugár, m magasság) felszíne 2 r 2 π+m 2 r π m 2 Henger (r sugár, m magasság) térfogata r 2 π m m 3 Gömb (r sugár) felszíne 4 r 2 π m 2 Gömb (r sugár) térfogata 4 r 3 π/3 m 3 Térfogat Háromszög (a oldal, m a magasság) területe

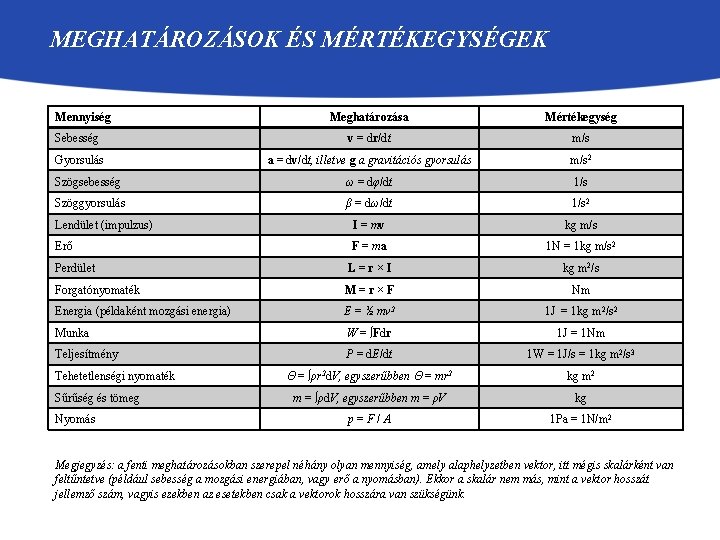
MEGHATÁROZÁSOK ÉS MÉRTÉKEGYSÉGEK Mennyiség Meghatározása Mértékegység Sebesség v = dr/dt m/s Gyorsulás a = dv/dt, illetve g a gravitációs gyorsulás m/s 2 Szögsebesség ω = dφ/dt 1/s Szöggyorsulás β = dω/dt 1/s 2 Lendület (impulzus) I = mv kg m/s Erő F = ma 1 N = 1 kg m/s 2 Perdület L=r×I kg m 2/s Forgatónyomaték M=r×F Nm Energia (példaként mozgási energia) E = ½ mv 2 1 J = 1 kg m 2/s 2 Munka W = ∫Fdr 1 J = 1 Nm Teljesítmény P = d. E/dt 1 W = 1 J/s = 1 kg m 2/s 3 Θ = ∫ρr 2 d. V, egyszerűbben Θ = mr 2 kg m 2 m = ∫ρd. V, egyszerűbben m = ρV kg p=F/A 1 Pa = 1 N/m 2 Tehetetlenségi nyomaték Sűrűség és tömeg Nyomás Megjegyzés: a fenti meghatározásokban szerepel néhány olyan mennyiség, amely alaphelyzetben vektor, itt mégis skalárként van feltűntetve (például sebesség a mozgási energiában, vagy erő a nyomásban). Ekkor a skalár nem más, mint a vektor hosszát jellemző szám, vagyis ezekben az esetekben csak a vektorok hosszára van szükségünk.

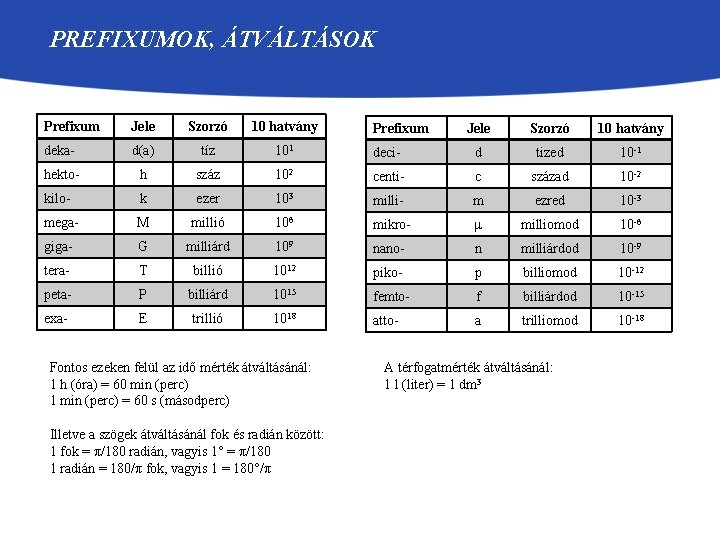
PREFIXUMOK, ÁTVÁLTÁSOK Prefixum Jele Szorzó 10 hatvány deka- d(a) tíz 101 hekto- h száz kilo- k mega- Jele Szorzó 10 hatvány deci- d tized 10 -1 102 centi- c század 10 -2 ezer 103 milli- m ezred 10 -3 M millió 106 mikro- μ milliomod 10 -6 giga- G milliárd 109 nano- n milliárdod 10 -9 tera- T billió 1012 piko- p billiomod 10 -12 peta- P billiárd 1015 femto- f billiárdod 10 -15 exa- E trillió 1018 atto- a trilliomod 10 -18 Fontos ezeken felül az idő mérték átváltásánál: 1 h (óra) = 60 min (perc) 1 min (perc) = 60 s (másodperc) Illetve a szögek átváltásánál fok és radián között: 1 fok = π/180 radián, vagyis 1° = π/180 1 radián = 180/π fok, vagyis 1 = 180°/π Prefixum A térfogatmérték átváltásánál: 1 l (liter) = 1 dm 3

GYAKORLAT I. Az alábbi vektorösszefüggések közül melyek helyesek, és melyek nem a vektor, illetve skalár tulajdonságok alapján? g+k=p g*k=p g×k=a g+k=p d*k=p g·k=μ g+k=μ g×k=μ g·k=x g×k=p g·k=μ g-k=p g-k=μ

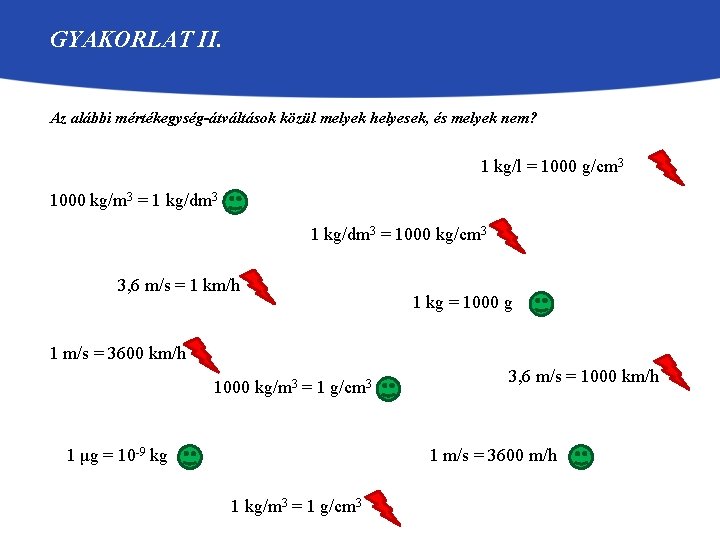
GYAKORLAT II. Az alábbi mértékegység-átváltások közül melyek helyesek, és melyek nem? 1 kg/l = 1000 g/cm 3 1000 kg/m 3 = 1 kg/dm 3 = 1000 kg/cm 3 3, 6 m/s = 1 km/h 1 kg = 1000 g 1 m/s = 3600 km/h 1000 kg/m 3 = 1 g/cm 3 1 μg = 10 -9 kg 3, 6 m/s = 1000 km/h 1 m/s = 3600 m/h 1 kg/m 3 = 1 g/cm 3

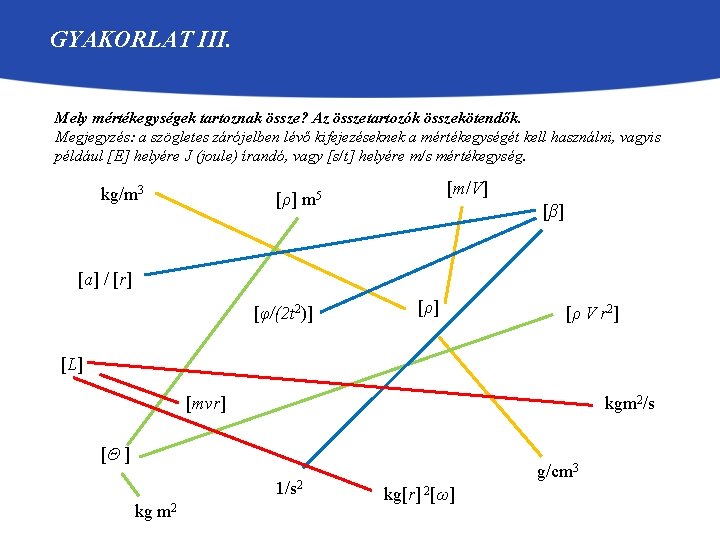
GYAKORLAT III. Mely mértékegységek tartoznak össze? Az összetartozók összekötendők. Megjegyzés: a szögletes zárójelben lévő kifejezéseknek a mértékegységét kell használni, vagyis például [E] helyére J (joule) írandó, vagy [s/t] helyére m/s mértékegység. kg/m 3 [m/V] [ρ] m 5 [β] [a] / [r] [φ/(2 t 2)] [ρ V r 2] [L] [mvr] kgm 2/s [Θ ] 1/s 2 kg m 2 g/cm 3 kg[r] 2[ω]

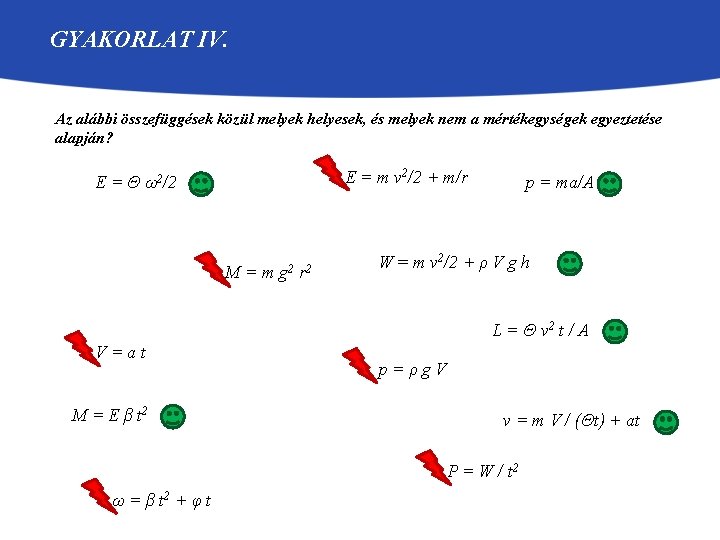
GYAKORLAT IV. Az alábbi összefüggések közül melyek helyesek, és melyek nem a mértékegységek egyeztetése alapján? E = m v 2/2 + m/r E = Θ ω2/2 M=m g 2 r 2 p = ma/A W = m v 2/2 + ρ V g h L = Θ v 2 t / A V=at M = E β t 2 p=ρg. V v = m V / (Θt) + at P = W / t 2 ω = β t 2 + φ t

GYAKORLAT V. Az adott fizikai összefüggéshez tartozik egy vektortulajdonságokat, és egy mértékegységeket egyeztető elem. Ezeket kellene összekötni! s = β r t 2/2 + ω0 r t N*m = kg*m 2/s 2 = kg*m/s 2 *m skalár = skalár 4 W = m * r · d 2 r/dt 2 kg*m 2 = kg/m 3*m 2*m 3 vektor = skalár*vektor × vektor |M| = Θβ W = N*m/s = kg*m 2/s 3 skalár = skalár 2 p = ρVg /A kg*m 2/s = kg*m*m/s = [Θ]*[ω] skalár = vektor · vektor P=F·v Pa = N/m 2 = kg/m 3*m/s 2/m 2 skalár = skalár 3/skalár L=mr×v m = m*1/s 2 *s 2+1/s *m*s skalár = skalár * vektor · vektor Θ = ∫ρr 2 d. V J = kg*m*m*1/s 2 = kg*m 2/s 2 skalár = skalár 4 + skalár 3

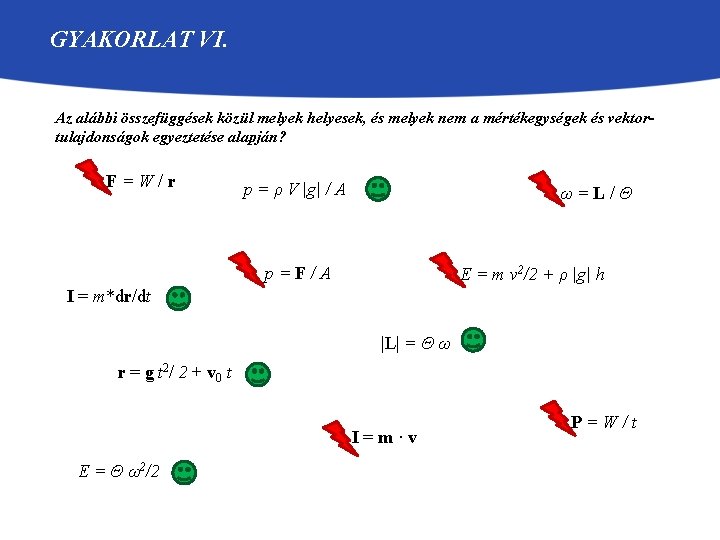
GYAKORLAT VI. Az alábbi összefüggések közül melyek helyesek, és melyek nem a mértékegységek és vektortulajdonságok egyeztetése alapján? F=W/r p = ρ V |g| / A ω=L/Θ p=F/A E = m v 2/2 + ρ |g| h I = m*dr/dt |L| = Θ ω r = g t 2/ 2 + v 0 t I=m·v E = Θ ω2/2 P=W/t

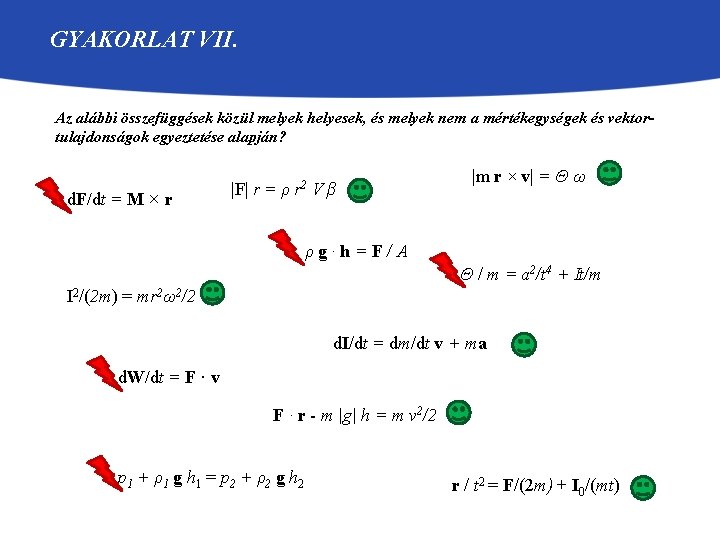
GYAKORLAT VII. Az alábbi összefüggések közül melyek helyesek, és melyek nem a mértékegységek és vektortulajdonságok egyeztetése alapján? d. F/dt = M × r |F| r = ρ r 2 V β |m r × v| = Θ ω ρg·h=F/A Θ / m = a 2/t 4 + It/m I 2/(2 m) = mr 2ω2/2 d. I/dt = dm/dt v + ma d. W/dt = F · v F · r - m |g| h = m v 2/2 p 1 + ρ1 g h 1 = p 2 + ρ2 g h 2 r / t 2 = F/(2 m) + I 0/(mt)

KÖSZÖNÖM A FIGYELMET!