A First Course in Stochastic Processes Chapter Two

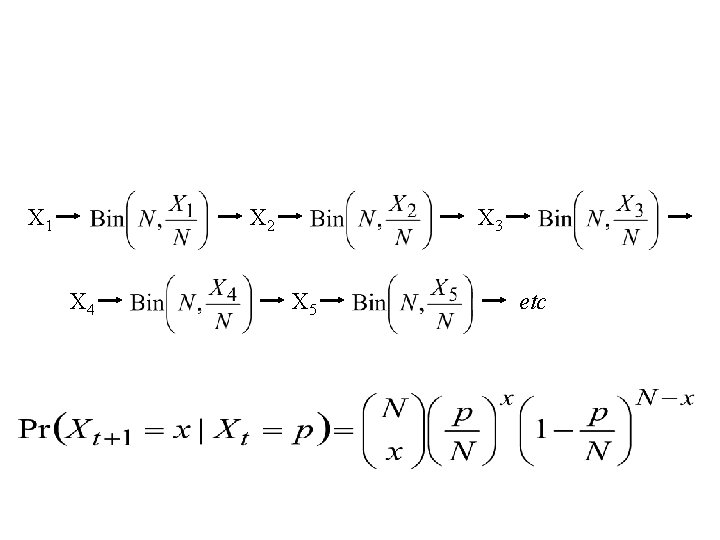














- Slides: 34

A First Course in Stochastic Processes Chapter Two: Markov Chains

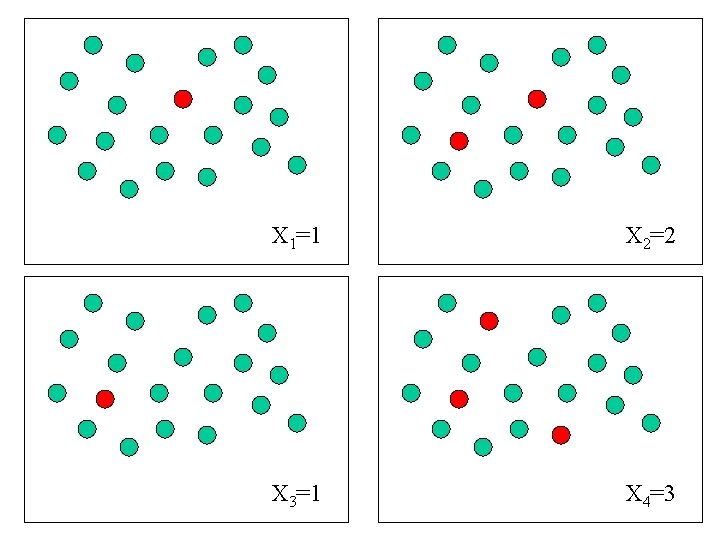
X 1=1 X 2=2 = X 3=1 X 4=3
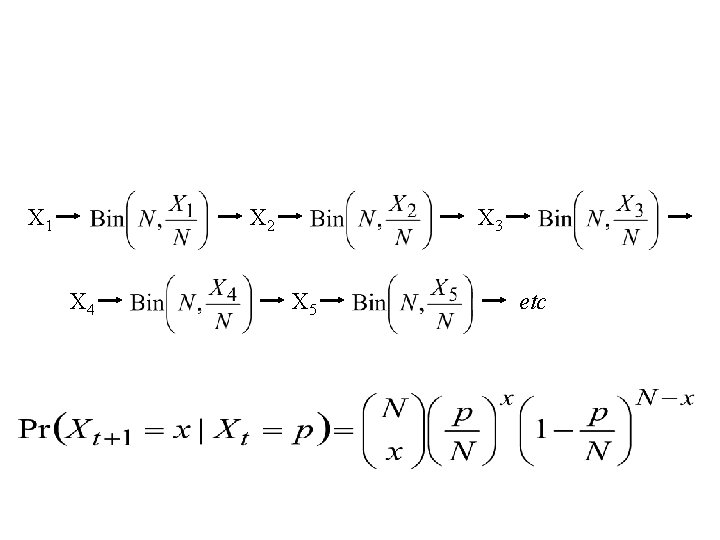
X 1 X 2 X 4 X 3 X 5 etc

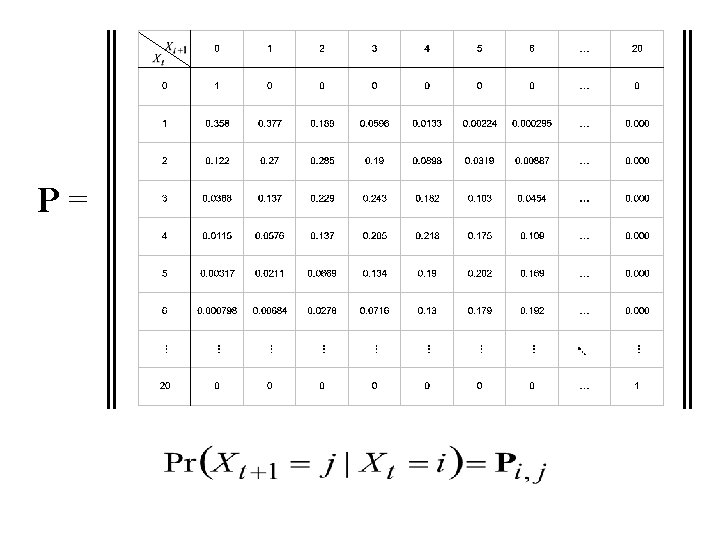
P=

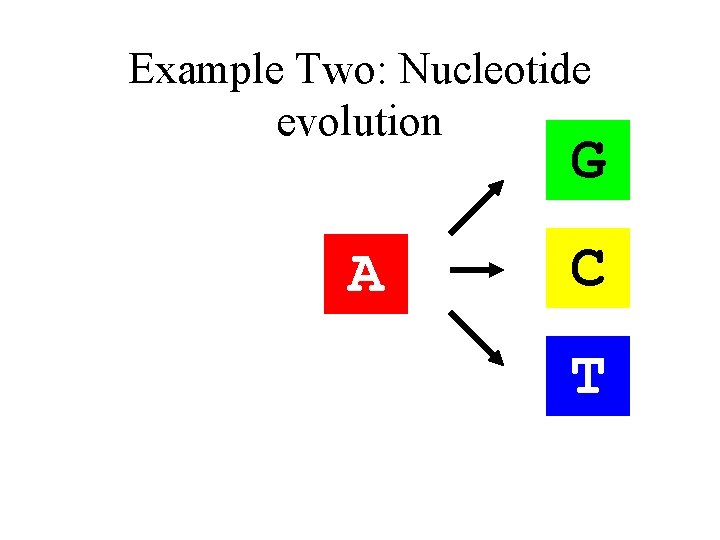
Example Two: Nucleotide evolution G A C T

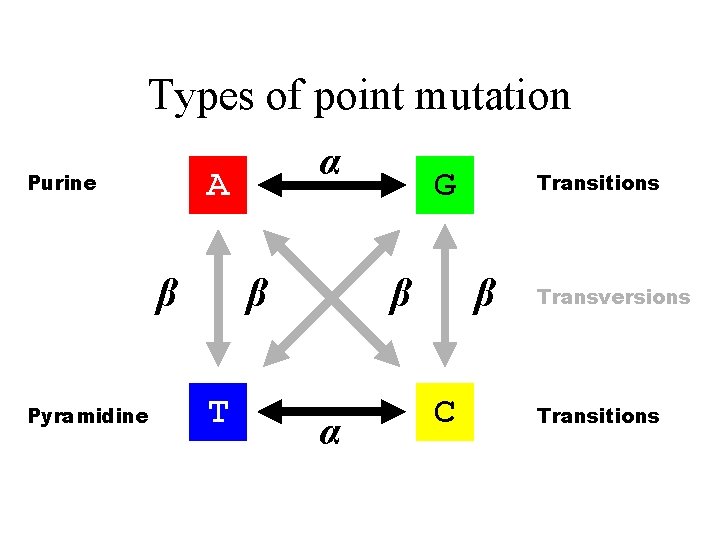
Types of point mutation A Purine β Pyramidine α β T G β α Transitions β C Transversions Transitions

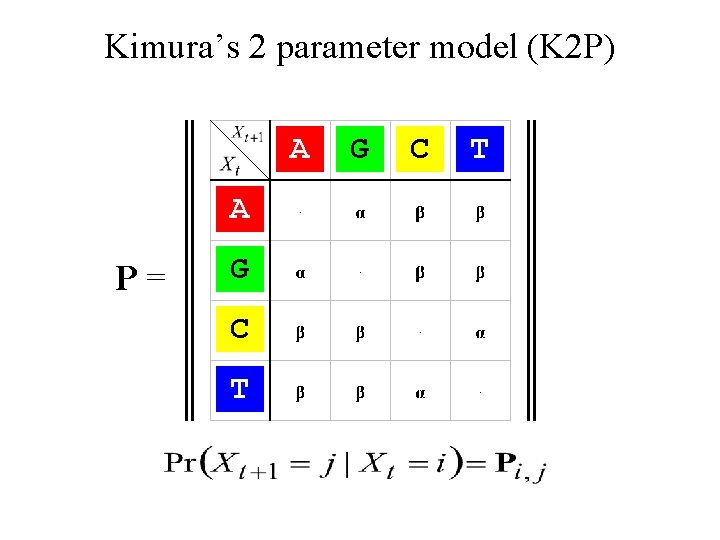
Kimura’s 2 parameter model (K 2 P) A A P= G C T

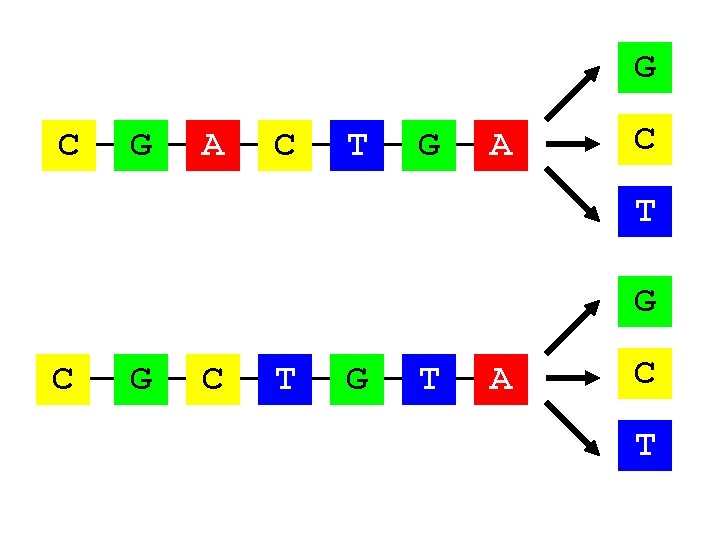
G C G A C T G A C G T C A T T G C T A C T

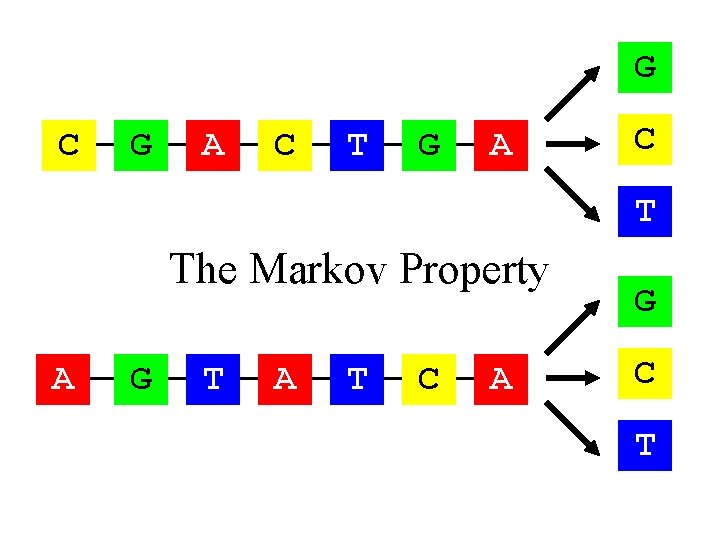
G C G A C T The Markov Property A G T A T C A G C T
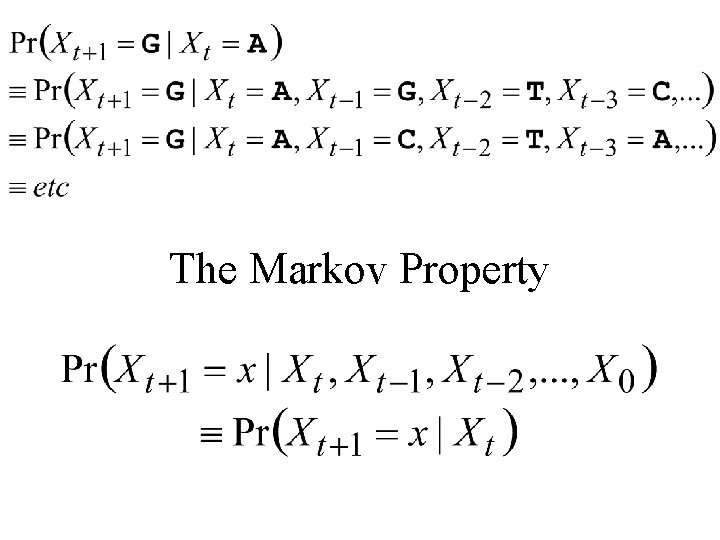
The Markov Property

Markov Chain properties accessible aperiodic communicate recurrent irreducible transient

Accessible A A P= G C T 0 G C T

Accessible A (and G) are no longer accessible from C (or T). A G C 0 0 T 0 0 A P= G C T

Accessible But C (and T) are still accessible from A (or G). A G C 0 0 T 0 0 A P= G C T

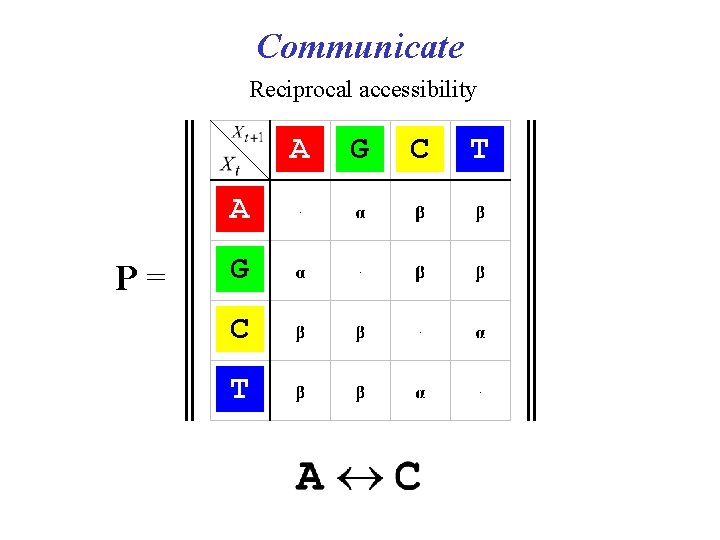
Communicate Reciprocal accessibility A A P= G C T

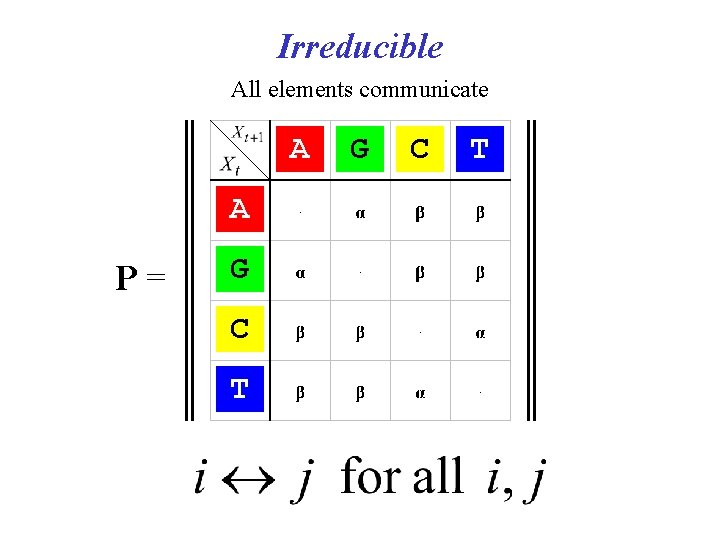
Irreducible All elements communicate A A P= G C T

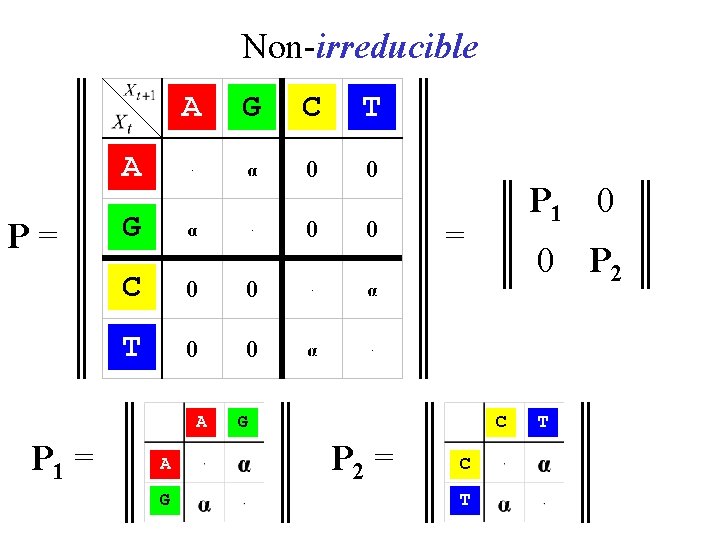
Non-irreducible A P= C T A 0 0 G 0 0 C 0 0 T 0 0 A P 1 = G A G P 1 0 = G 0 P 2 C P 2 = C T T

Repercussions of communication • Reflexivity • Symmetry • Transitivity

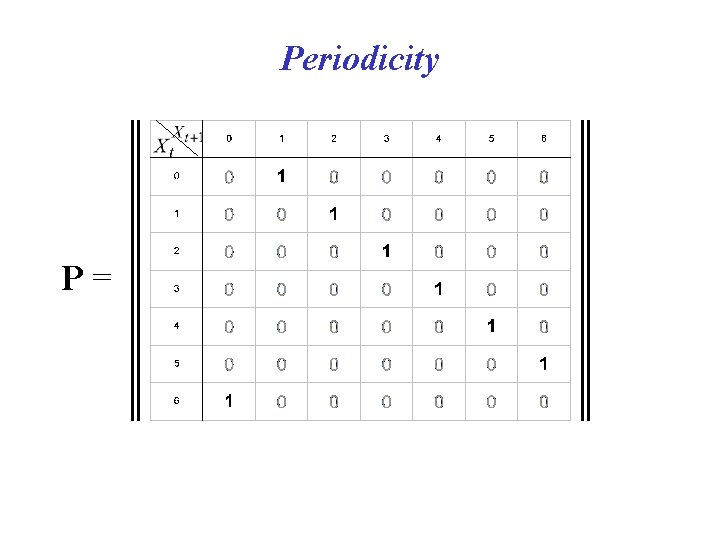
Periodicity P=

Periodicity • The period d(i) of an element i is defined as the greatest common divisor of the numbers of the generations in which the element is visited. • Most Markov Chains that we deal with do not exhibit periodicity. • A Markov Chain is aperiodic if d(i) = 1 for all i.

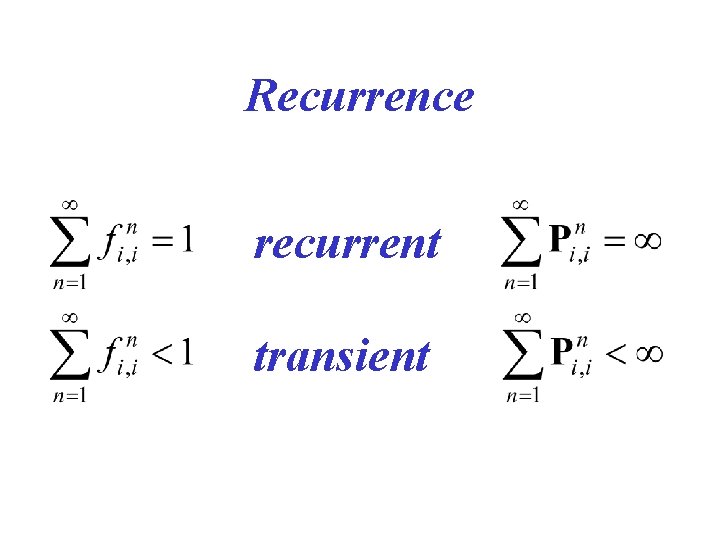
Recurrence recurrent transient

More on Recurrence • and i is recurrent then j is recurrent • In a one-dimensional symmetric random walk the origin is recurrent • In a two-dimensional symmetric random walk the origin is recurrent • In a three-dimensional symmetric random walk the origin is transient

Markov Chain properties accessible aperiodic communicate recurrent irreducible transient

Markov Chains Examples

X 1=1 X 2 X 4 X 3 X 5 etc

P=

Diffusion across a permeable membrane (1 D random walk)

Brownian motion (2 D random walk)

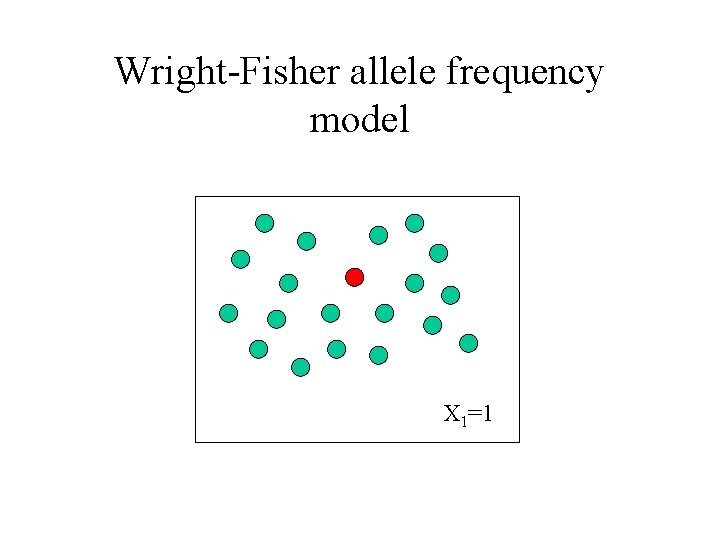
Wright-Fisher allele frequency model X 1=1

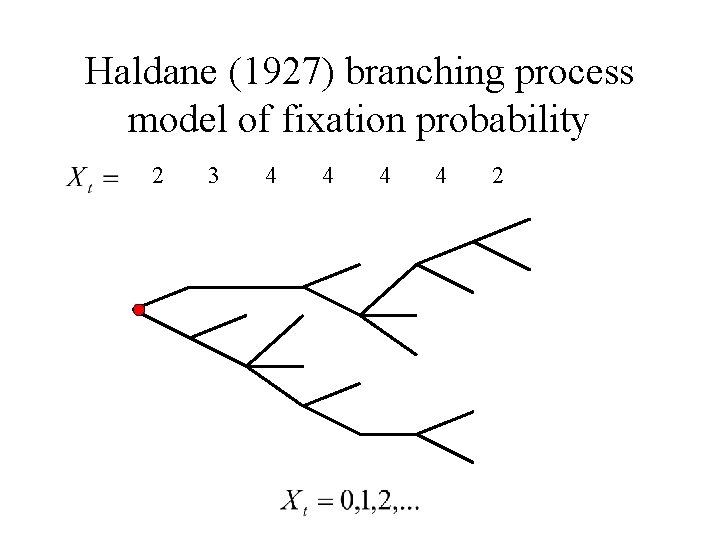
Haldane (1927) branching process model of fixation probability 2 3 4 4 2

Haldane (1927) branching process model of fixation probability

Haldane (1927) branching process model of fixation probability Pi, j = coefficient of sj in the above generating function

Haldane (1927) branching process model of fixation probability Probability of fixation = 2 s

Markov Chain properties accessible aperiodic communicate recurrent irreducible transient