A Few Simple Applications to Cryptography Louis Salvail

A Few Simple Applications to Cryptography Louis Salvail BRICS, Aarhus University

QKD: An “Application” of Non. Cloning 1 st attack: 102344578907 +x++xx+xx++x++ 1010010110 a digression: pick. First, random bases, measure and store the 102344578908 x++x+x+xx 10010110001110 outcome. 102344578909 ++xx+xx+x+++x+ 11010111001010 Wiesner’s unforgeable quantum cash 102344578910 x+xxx++x+x+++x 01101010011000 2 nd attack: 102344578911 102344578912 102344578913 102344578914 102344578915 +x++xx+x+x+xx++x++ xx+x+++x+ +x+x+++xx+x++x x+++xx+x+x+++x 0011110011010110100 01010010011101 01010111101000 1011010111 00 1 1 011 001 0 0 0 11 0 1 102344578911

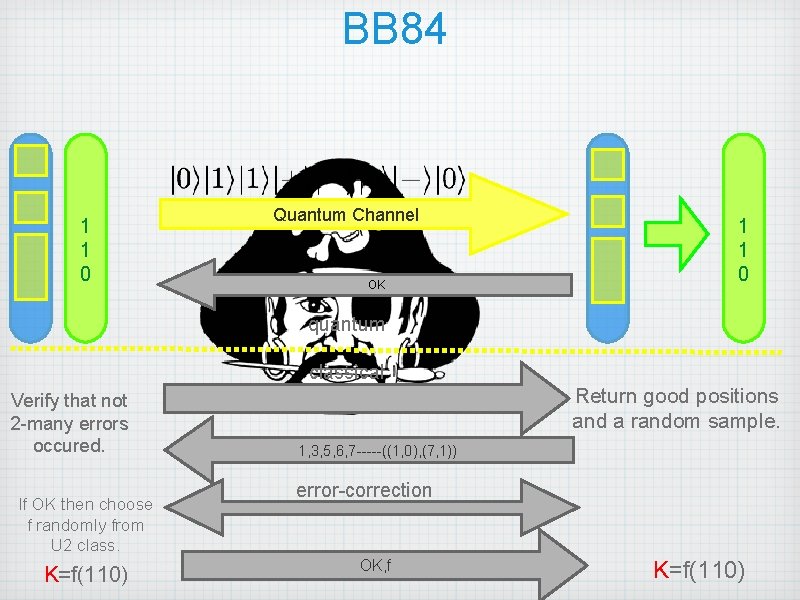
BB 84 0 1* 1 1 0* Quantum Channel OK quantum 0 1* 1 0 1 1* classical Verify that not 2 -many errors occured. If OK then choose f randomly from U 2 class. K=f(110) Return good positions and a random sample. 1, 3, 5, 6, 7 -----((1, 0), (7, 1)) error-correction OK, f K=f(110)

Hardware This is how a QKD set-up looked like a few years ago. And now: photodetector: photon source

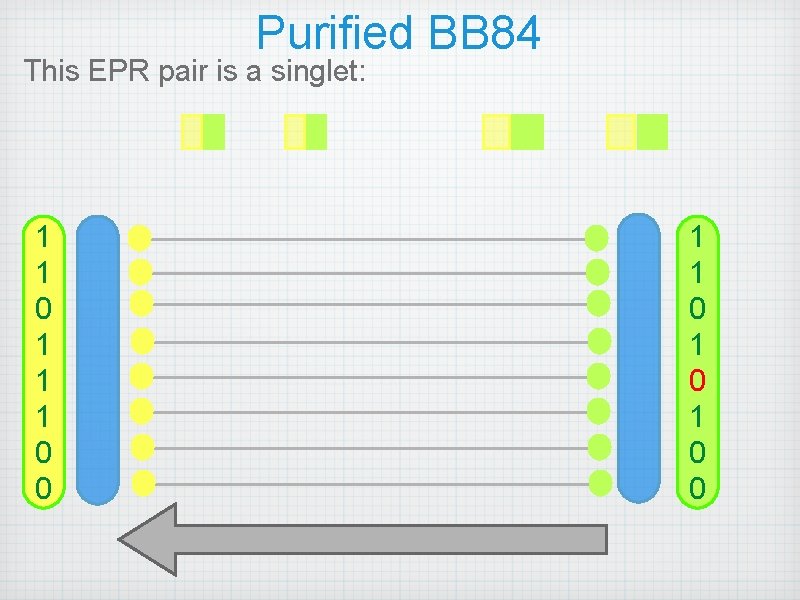
Purified BB 84 This EPR pair is a singlet: 1 1 0 1 1 1 0 0 1 1 0 1 0 0

Encrypting Qubits Suppose we want to encrypt a qubit under a classical secret-key K, such that: The cipher state alone does not reveal any information on the state of the qubit. Using K, the qubit can be perfectly reconstructed from the cipher state.

Encryption/Decryptio n We suppose that encryption is performed by a family of unitary transforms {UK}K indexed by secret-key K. The simplest form is that upon qubit |φ>, the cipher state is generated as: |e. K(φ)> = UK |φ>. Decryption is performed by running UK backward (its complex conjugate transposed).

Privacy means that given only the cipher state |e. K(φ)>, no information can be extracted about the state |φ>. This can be captured by enforcing that the quantum state produced by an encryption under a uniform and random choice for K is independent of |φ>. This would mean that an eavesdropper ignorant of K always sees the same state. No measurement can therefore distinguish the encryptions of any 2 states.

The State Available to the Eavesdropper As we have seen, the state available to the adversary when |φ> is encrypted is the mixed state corresponding to the encryption of |φ> over all keys: An encryption scheme is therefore said to be private if:

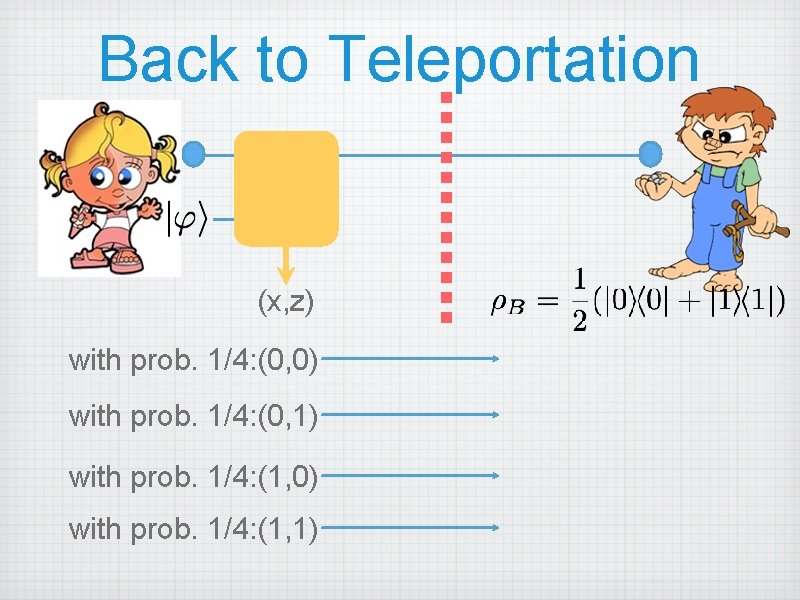
Back to Teleportation (x, z) with prob. 1/4: (0, 0) with prob. 1/4: (0, 1) with prob. 1/4: (1, 0) with prob. 1/4: (1, 1)

Encryption/Decryptio n Suppose Alice and Bob share K ∈ {0, 1}×{0, 1}: If K=(0, 0) If K=(0, 1) If K=(1, 0) If K=(1, 1) Since XX=ZZ=-YY=I, Bob decrypts by applying the same transform indicated by K:

In General It can be shown that 2 classical bits are necessary in order to encrypt with perfect privacy (and with perfect decryption) an arbitrary qubit. If the possible states of the qubit are restricted to some special sets then 1 classical could be sufficient. For the encryption of qubits with only statistical privacy and almost perfect descryption, a single classical bit per qubit is asymptotically sufficient.

First Special Case Suppose the possible states of the qubit are { |0>, |1> }. The situation is now classical and the one-time-pad (one bit per qubit) provides perfect privacy. Notice that the encryption of these 2 states using X with probability 1/2 is exactly the same as the one-time-pad.

Second Special Case Suppose the qubit to encrypt is of the form |φ> = a|0> + b|1> where a, b are real numbers. Now, observe that: So, only complex amplitude states require 2 bits of key.

Committing a Qubit Teleportation also allows to see how one can commit on a qubit given only a classical commitment scheme. Suppose the scheme allows for committing on a pair of classical bits. Encrypt |φ> using a random key K. classical commitment of K

Encrypting Classical Messages in Quantum States Consider the symmetric encryption of classical messages in quantum states. We’ll get a simple encryption scheme that resists “better” to known plaintext attacks than any classical scheme. It is based upon what is called an uncertainty relations.

Hadamard Transform Remember that: Let’s define the following 2 Von Neumann measurements on n qubits (computational & diagonal basis): Associated to |φ>, we can define the 2 probability distributions for the outcomes of M+ and Mx when applied to |φ>:

Uncertainty Relation The following uncertainty relation has been shown by Maassen and Uffink. We shall denote by H(pφ) and H(qφ) the Shannon entropy for distributions pφ(x) and qφ(x) respectively. Theorem: For any n-qubit state |φ>, it is the case that H(pφ) + H(qφ) ≥ n.

An equivalent uncertainty relation Suppose that a source S sends a quantum state chosen as follows: Pick x in {0, 1}n at random, With prob. 1/2 send |x>, With prob. 1/2 send H⊗n|x>. Theorem: Let X be the random variable describing the choice made by S above. Let Y be the random variable for the outcome of an arbitrary measurement applied to the state sent by S. Then, for any outcome y: H(X|Y=y) ≥ n/2.

Encryption Scheme The key K=(p, h) where p ∈ {0, 1} and h ∈ n {0, 1}. The encryption of message m is done the following way: • c : = m ⊕ p • If h=0 then send |c> This is called the Hn-cipher Else send H⊗n|c>. Notice that the scheme is private since the message m is one-time-padded. This is a (n, n+1)-encryption scheme: it encrypts n-bit messages using n+1 bit of keys.

Known Plaintext Attacks In a known plaintext attack, the adversary gets the ciphertext(cipherstate), the plaintext and wants to extract as much information as possible on the secret-key. Theorem: Any classical (n, n+1)-cipher is such that H(K| c, m) ≤ 1. Theorem: The (n, n+1)-quantum cipher Hn is such that H((p, h) | (H⊗n)h | |m⊕p>, m)≥ n/2. Given m and the situation is equivalent to Proof sketch: distinguishing among {|p>, H⊗n|p>}p∈{0, 1}n. We have seen that the entropy on p is at least n/2. In addition, it can be shown that the extra bit of key h is perfectly hidden. It follows that: H((p, h) | View) ≥ n/2+1.

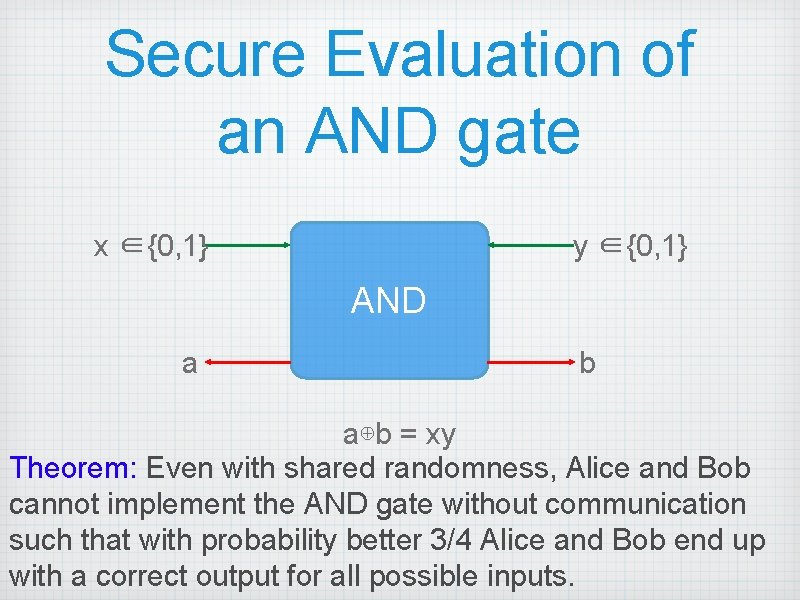
Secure Evaluation of an AND gate x ∈{0, 1} y ∈{0, 1} AND a b a⊕b = xy Theorem: Even with shared randomness, Alice and Bob cannot implement the AND gate without communication such that with probability better 3/4 Alice and Bob end up with a correct output for all possible inputs.

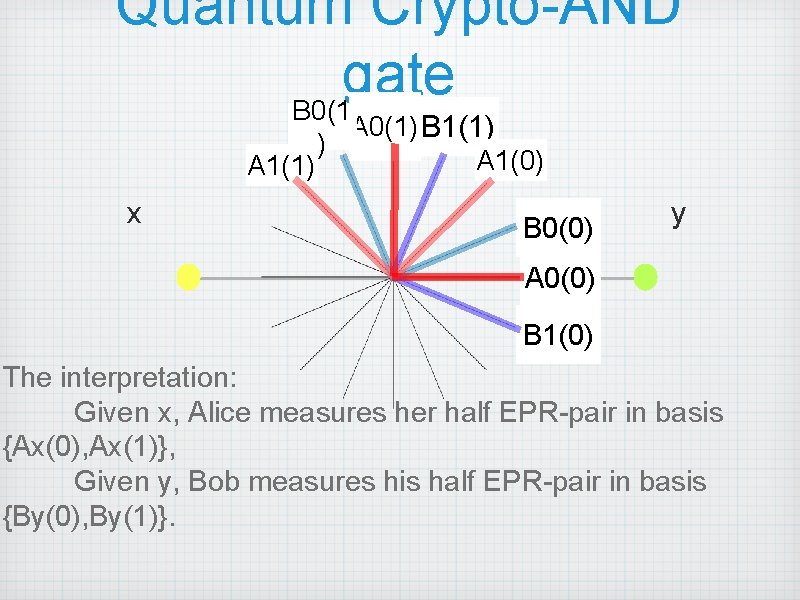
Quantum Crypto-AND gate B 0(1 A 0(1) B 1(1) ) A 1(0) A 1(1) x B 0(0) y A 0(0) B 1(0) The interpretation: Given x, Alice measures her half EPR-pair in basis {Ax(0), Ax(1)}, Given y, Bob measures his half EPR-pair in basis {By(0), By(1)}.

Why it Works Let p(x, y) be the error-probability when Alice inputs x and Bob inputs y:

Conclusion With shared-EPR pairs, Alice and Bob can end up with an additive sharing for the AND of their bits without communication and with probability cos 2(π/8)≈0. 85. This is significantly better than what is achievable by any classical strategy using shared randomness. Quantum entanglement is therefore more than classical shared randomness!! This was originally shown by Bell using a different method called the Bell inequalities.