A Faster Algorithm for Computing the Principal Sequence

A Faster Algorithm for Computing the Principal Sequence of Partitions of a Graph Vladimir Kolmogorov University College London

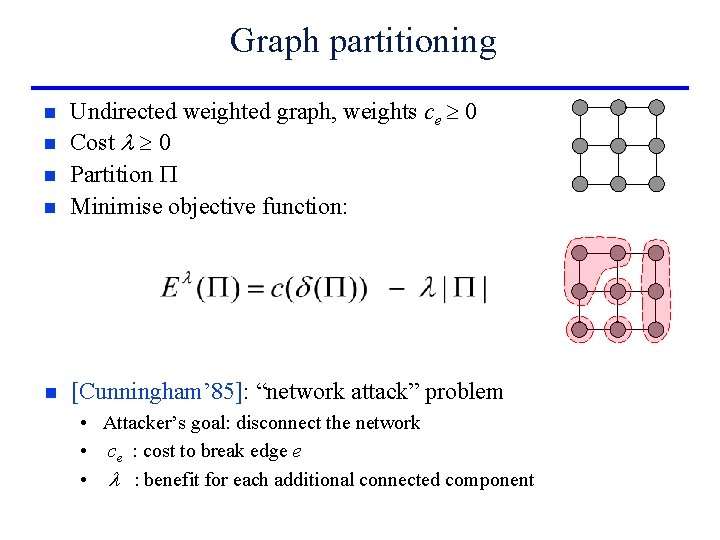
Graph partitioning n Undirected weighted graph, weights ce 0 Cost l 0 Partition P Minimise objective function: n [Cunningham’ 85]: “network attack” problem n n n • Attacker’s goal: disconnect the network • ce : cost to break edge e • l : benefit for each additional connected component

Principal sequence of partitions n Increase l from 0 to + : • Nested partitions • Principal sequence of partitions [Narayanan’ 91] n Network strength:

Principal sequence of partitions n Applications: • Network reliability • Physics: computing partition function of Potts model in the infinite state limit [d’Auriac et al. ’ 02] • Image partitioning? ?

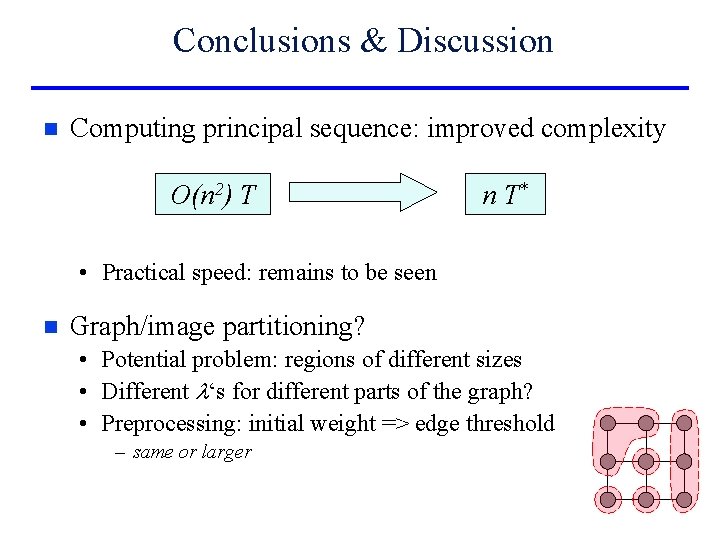
Graph partitioning: Algorithms n Fixed l (network attack) [Narayanan’ 91, Baranona’ 92, d’Auriac et al. ’ 02] n. T n l 1 (network strength) [Cheng&Cunnigham’ 94 (memory!)] , [Gabow’ 98] n T* n All l‘s (principal sequence) [Narayanan’ 91] O(n 2) T THIS WORK n : # of nodes T : maxflow algorithm m : # of edges T* : parametric maxflow n T*

Parametric maxflow n Minimise for all l’s: • Terms Vuv(xu, xv) – submodular • Unary terms Au(l): non-decreasing functions of l n n Nested sequence of solutions [Gallo, Grigoriadis, Tarjan’ 89]: same worst-case complexity as for a single maxflow - O(nm log(n 2/m))

Graph partitioning: Algorithms n Fixed l (network attack) [Narayanan’ 91, Baranona’ 92, d’Auriac et al. ’ 02] n. T n l 1 (network strength) [Cheng&Cunnigham’ 94 (memory!)] , [Gabow’ 98] n T* n All l‘s (principal sequence) [Narayanan’ 91] O(n 2) T n THIS WORK Outline: • Part I: review of [Barahona’ 92] (fixed l) • Part II: generalising [Barahona’ 92] (fixed l) • Part III: parametric algorithm (all l’s) n T*

Part I: Review of [Barahona’ 92] algorithm Solving network attack for fixed l

Relation to set minimisation n Cost of partition P: n Cost of subset A V :

Polymatroid P( f l) [Edmonds’ 70] n Set of linear lower bounds: n Non-empty subset A is tight for y P( f l) if

Optimality condition y P( f l) and all subsets A P are tight P minimises E l()

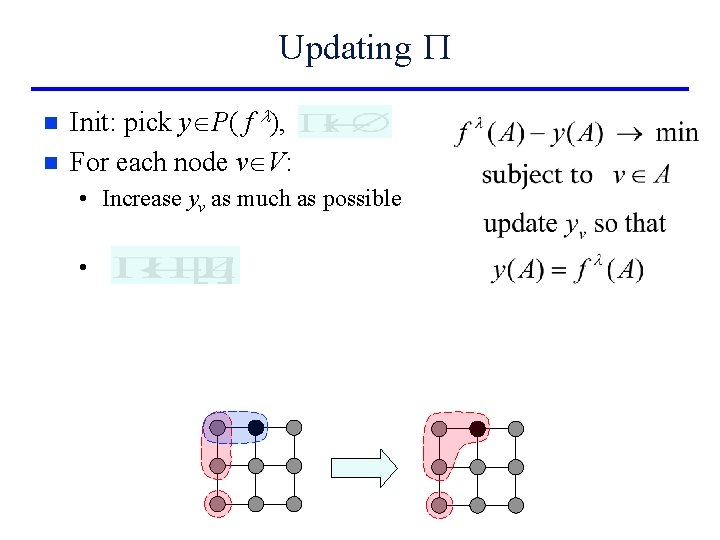
Greedy algorithm [Edmonds’ 70]: compute maximal vector y P( f l) n n Init: pick y P( f l) For each node v V: • Increase yv as much as possible v

Greedy algorithm [Edmonds’ 70]: compute maximal vector y P( f l) n n Init: pick y P( f l) For each node v V: • Increase yv as much as possible v A

Updating P n n Init: pick y P( f l), For each node v V: • Increase yv as much as possible •

Summary n Introduced: • Submodular function f l • Polymatroid P( f l) • Tight subsets A for y P( f l) n Greedy algorithm: compute maximal vector y P( f l) • Invariants: – y P( f l) – Subsets A P are tight • In the end P complete global minimum • n min cuts

Part II: Generalising greedy algorithm

Non-greedy algorithm n n Init: pick y P( f l) For each node v V: [optional] n Correctness: see paper • y P( f l) • Subsets A P are tight A

Part III: New parametric algorithm Solving network attack for all l‘s

Overview n Maintain families {yl}l and {Pl}l for all l 0 [optional] n Need to solve parametric problem for all l’s

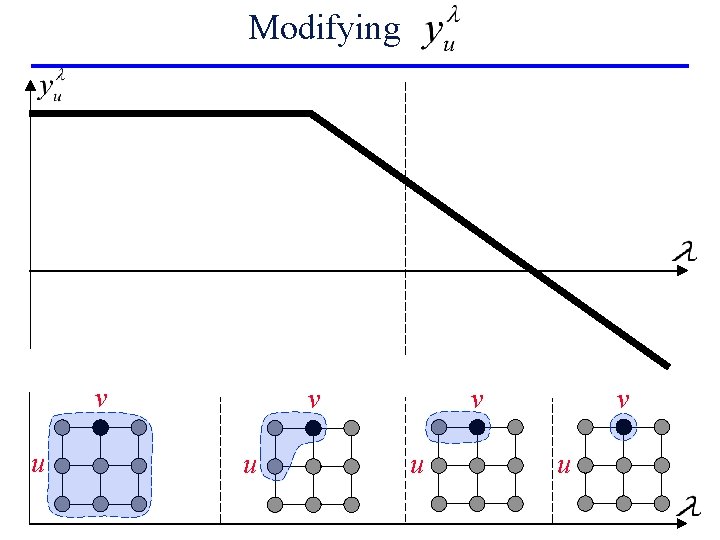
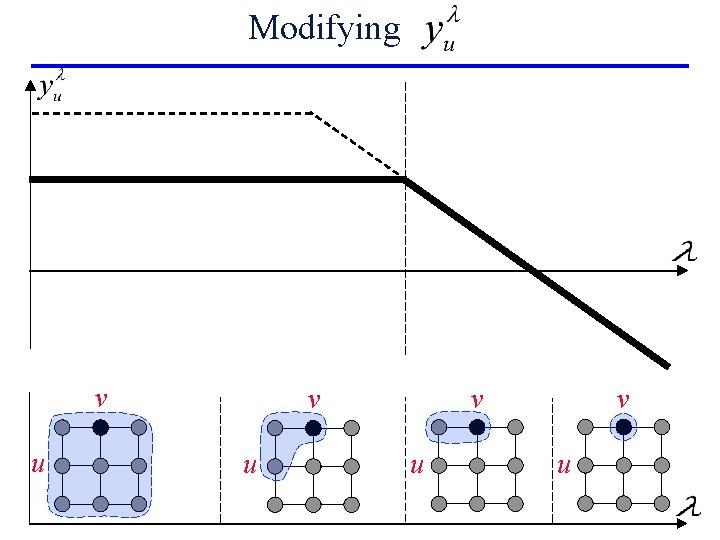
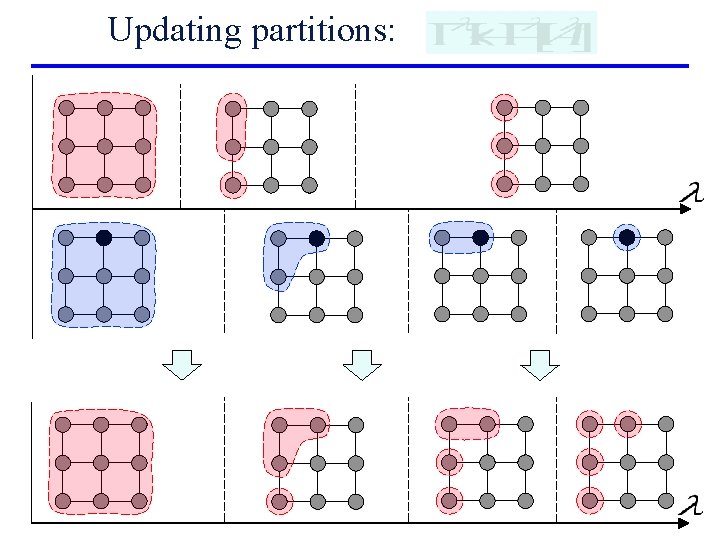
Naïve idea: use greedy algorithm n Does not quite work. . . • Functions yvl – piecewiselinear with many breakpoints • Non-monotonic!

[Cheng&Cunningham’ 94] n n Decreasing sequence l 1 > l 2 >. . . > lk Solve for li (n min cuts), use final y as initialisation for li+1 • k maxflow problems for each node u are parametric n n To exploit it, need to store n graphs of size O(n+m)! Can compute network strength, but not principal sequence

Use non-greedy algorithm! n Functions - monotonic piecewise -linear with one breakpoint [optional]

Modifying v u v v u u v u

Modifying v u v v u u v u

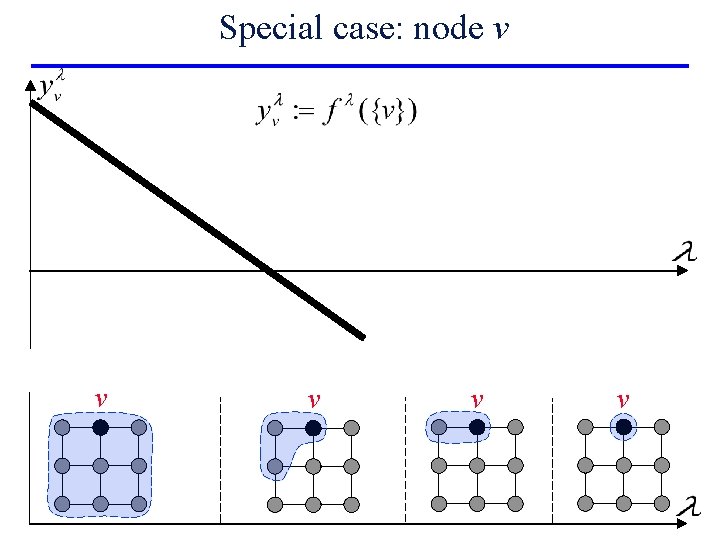
Special case: node v v v

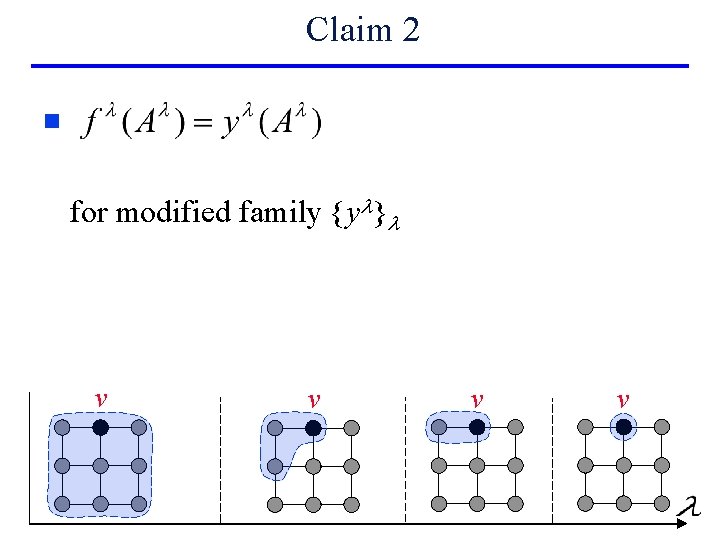
Correctness n Need to show: for each l – non-greedy algorithm • Claim 1: updating y l preserves optimality of Al • Claim 2:

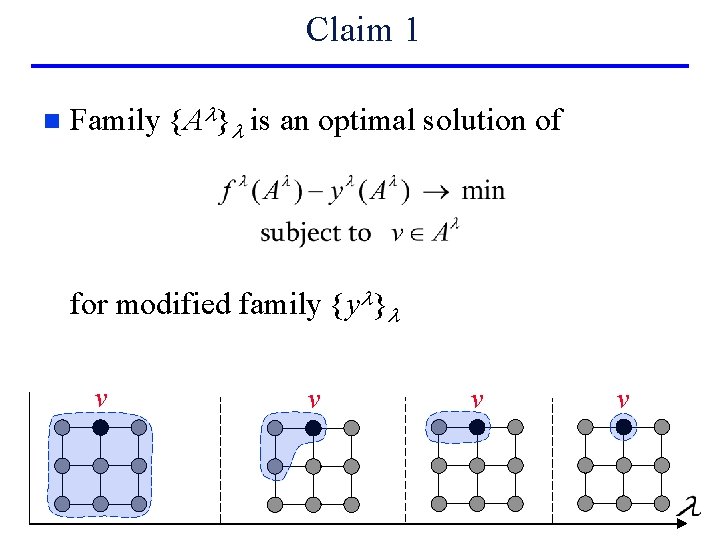
Claim 1 n Family {Al}l is an optimal solution of for modified family {yl}l v v

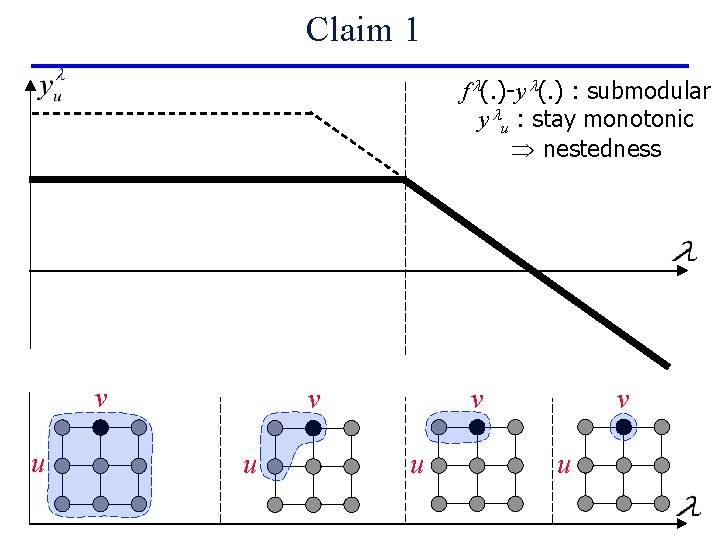
Claim 1 f l(. )-y l(. ) : submodular y lu : stay monotonic nestedness v u v v u u v u

Conclusions & Discussion n Computing principal sequence: improved complexity O(n 2) T n T* • Practical speed: remains to be seen n Graph/image partitioning? • Potential problem: regions of different sizes • Different l‘s for different parts of the graph? • Preprocessing: initial weight => edge threshold – same or larger

Graph partitioning & submodularity n X: subset of edges n k(X)=# connected components in (V, X) • Supermodular n Function is submodular • Can be minimised in polynomial time • Minimum corresponds to “valid” partition P •

Updating partitions:

Claim 2 n for modified family {yl}l v v